落谷P1443 马的遍历 题解

题目如下
题目描述
有一个 n×m 的棋盘，在某个点 (x,y) 上有一个马，要求你计算出马到达棋盘上任意一个点最少要走几步。

输入格式
输入只有一行四个整数，分别为 n,m,x,y。

输出格式
一个 n×m 的矩阵，代表马到达某个点最少要走几步（不能到达则输出 −1）。

好像是一个bfs算法的经典题目

根据输出格式我们可以得知，题目要求我们输出这样一个m*n的棋盘数组，在对应位置输出我们从起始位置（x,y)，通过“马走日”的走法到达的最小步数

我们根据“马走日”的规则总结出每次可能移动的坐标，

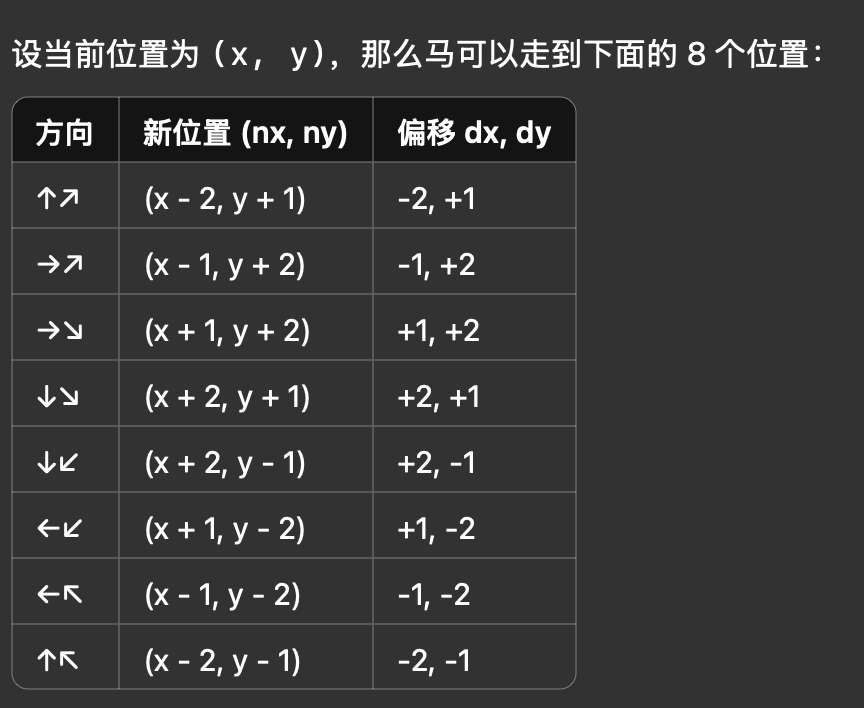
因此，我们首先构造两个一维数组分别来描述每次移动横坐标与纵坐标的变化，注意横纵坐标总是一一对应的这样才能保证移动的坐标正确

接着我们来定义一下结构体

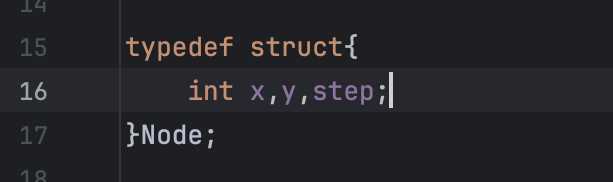
由横纵坐标和步数构成；

声明一下队列

‼️注意是一维的数组，每个单位包含一组Node；

bfs算法核心逻辑

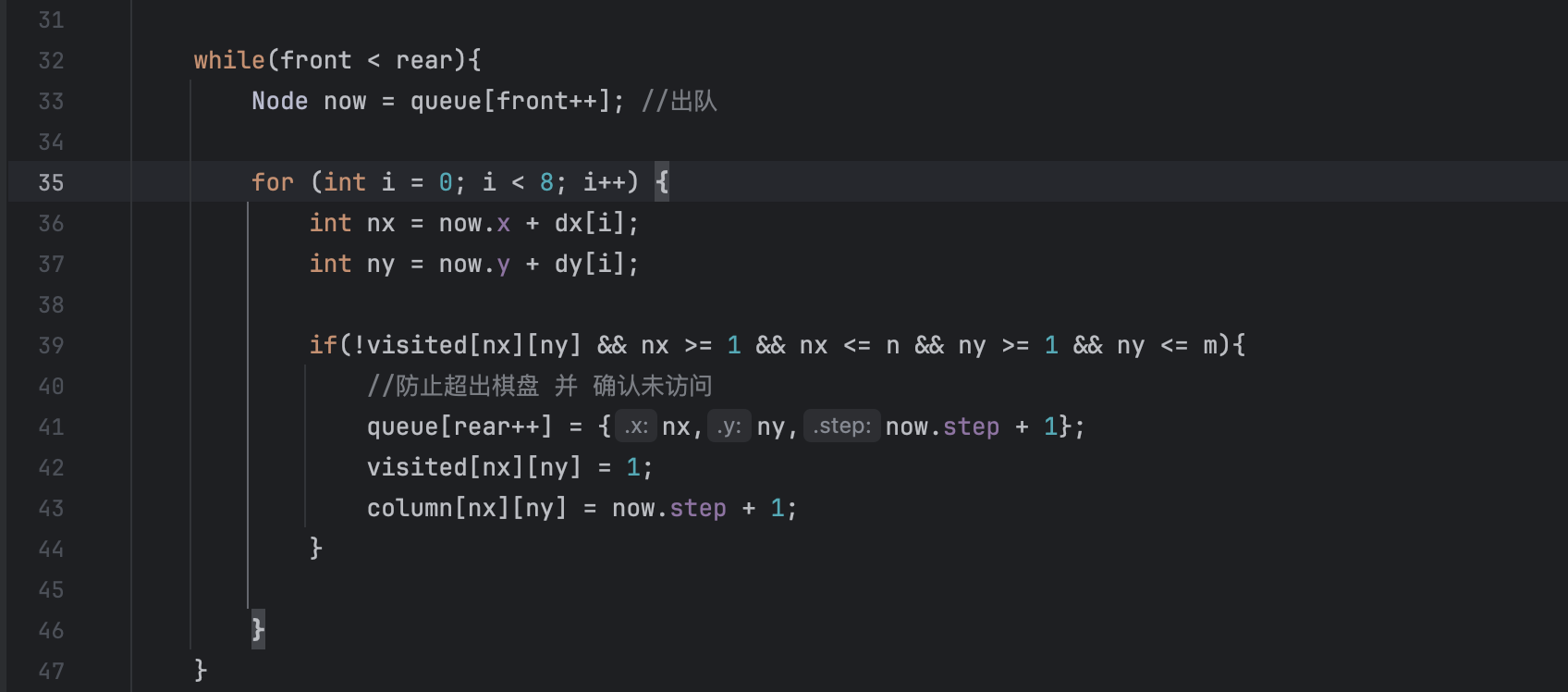
在队列不为空的前提下进行搜索，
• 从队首取出一个节点（出队），赋值给 now
• 根据“马走日”确定当前搜索的坐标
• 包含当前位置坐标 now.x, now.y 和从起点到这里的步数 now.step
• front++ 实现出队，移动头指针

完整代码如下
`#include <stdio.h>

include <string.h>

define MAXN 401

//马走日所以坐标的改变所有可能性如下
//一一对应坐标的改变
int dx[8] = {-2,-1,1,2,2,1,-1,-2};
int dy[8] = {1,2,2,1,-1,-2,-2,-1};

int column[MAXN][MAXN];
int visited[MAXN][MAXN];

typedef struct{
int x,y,step;
}Node;

void BFS(int n, int m, int x, int y ){ //没有返回值

Node queue[MAXN * MAXN]; //一维数组，最多能存 MAXN × MAXN 个 Node

int front = 0, rear = 0;
//初始化
memset(column, -1, sizeof(column));
memset(visited, 0, sizeof(visited));

queue[rear++] = (Node){x, y, 0}; //入队
visited[x][y] = 1; //已访问
column[x][y] = 0; //到达自身需要0步

while(front < rear){
    Node now = queue[front++]; //出队

    for (int i = 0; i < 8; i++) {
        int nx = now.x + dx[i];
        int ny = now.y + dy[i];

        if(!visited[nx][ny] && nx >= 1 && nx <= n && ny >= 1 && ny <= m){
            //防止超出棋盘 并 确认未访问
            queue[rear++] = {nx,ny,now.step + 1};
            visited[nx][ny] = 1;
            column[nx][ny] = now.step + 1;
        }

    }
}
int i,j;
for(i = 1; i <= n; i++){
    for(j = 1; j <= m; j++) {
        printf("%d ", column[i][j]);
    }
    printf("\n"); //输出完每一行后需换行
}

}
int main(){
int n, m, x ,y;
scanf("%d%d%d%d",&n, &m, &x, &y);
BFS(n, m, x ,y);
return 0;
}

`
其实我也刚刚学，是不是有一点学会了，学费了