快排解决 topK/中位数 问题

前言

经常会有这种问题：
1.一个100万的无序数组，在接近复杂度内找到其中位数。
2.一个100万的无序数组，找到其第 K 大的数。

这种问题最常见，也最经常被问到！也有很多对应的解决方法。这里给出一种用快排来解决问题的方法！

快排

快排的性能在所有排序算法里面是最好的，数据规模越大快速排序的性能越优。快排在极端情况下会退化成 O(n^2) 的算法，因此假如在提前得知处理数据可能会出现极端情况的前提下，可以选择使用较为稳定的归并排序。

快排本质上是一种分治策略，在一次循环结束，会有哨兵把数组分成前半部分与后半部分。且以哨兵为界前半部分都不大于（小于）后半部分。

• 如果哨兵恰好处于数组的中部时候那么哨兵就是整个数组的中位数。
• 无论那次循环，哨兵都是整个数组的 topK（这里哨兵下标为K）

实现

package main

import (
	"fmt"
)

func getTopK(arr []int, k, left, right int) int {
	if left >= right {
		return arr[left]
	}

	tmp := arr[left]
	lpos := left
	rpos := right

	for lpos < rpos {
		for ; lpos < rpos && arr[rpos] >= tmp; rpos-- {
		}

		if lpos < rpos {
			arr[lpos] = arr[rpos]
			lpos++
		}

		for ; lpos < rpos && arr[lpos] <= tmp; lpos++ {
		}

		if lpos < rpos {
			arr[rpos] = arr[lpos]
			rpos--
		}
	}

	arr[lpos] = tmp
	if lpos == k {
		return arr[lpos]
	} else if lpos < k {
		return getMid(arr, k, lpos+1, right)
	} else {
		return getMid(arr, k, left, lpos-1)
	}
}


func main() {
	arr := []int{1, 3, 8, 2, 6, 9, 0, 5}
	for i := 0; i < len(arr); i++ {
		fmt.Printf("top %d is %d\n", i, getTopK(arr, i, 0, len(arr)-1))
	}
}

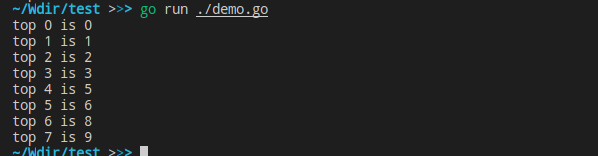
运行结果：