软件工程 - 个人项目
软件工程 - 个人项目作业
| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 2020春季计算机学院软件工程(罗杰 任健) |
| 这个作业的要求在哪里 | 个人项目作业 |
| 我在这个课程的目标是 | 学习软件工程的开发知识,培养工程化开发能力 |
| 这个作业在哪个具体方面帮助我实现目标 | 通过实操掌握PSP开发基础 |
1 概览
教学班级:006
项目地址:https://github.com/sinoyou/Software_Intersection
2 PSP2.1 分析
| PSP 2.1 | 个人软件阶段 | ||
|---|---|---|---|
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 120 | 150 |
| · Design Spec | · 生成设计文档 | 60 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | - | - |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 20 |
| · Design | · 具体设计 | 60 | 40 |
| · Coding | · 具体编码 | 120 | 150 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 240 | 210 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 60 | 50 |
| · Size Measurement | · 计算工作量 | 5 | 5 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 15 | 30 |
| 合计 | 750 | 725 |
3 解题思路
题目描述
- 题目需求为,给定若干直线(以两个点确定一条直线的方式给出,点的坐标必须为整数),求其交点的数量。
- 考虑性能情况下:直线条数
0 <= N <= 500000 - 交点个数
0 <= h <= 5000000 - 运行时长60s
数学模型
两个不同的点决定一条直线,给定点\((x_1, y_1)\)和\((x_2, y_2)\),可以得出一条直线的形式为\(ax + by + c = 0\)(其中,a和b不能够同时为0):
- \(a = y_1 - y_2\)
- \(b = x_2 - x_1\)
- \(c = x_1y_2 - x_2y_1\)
对于两条直线\(a_1x+b_1y+c_1=0\)和\(a_2x+b_2y+c_2=0\),根据运算,可以得到交点的表达式为:
程序实现
计算机以离散数据形式处理内容,虽然给定的点坐标为整数,但其交点不一定为整数。因此,本问题中需要考虑小数问题,在分析了数学模型的公式形式后,权衡C++库中的默认double、float类尚存在一定的精度误差,因此我决定设计自定义的分数类Rational用于数据的记录,并自定义分数支持的四则运算符和比较操作,以支持该问题所需的操作。
4 模型设计
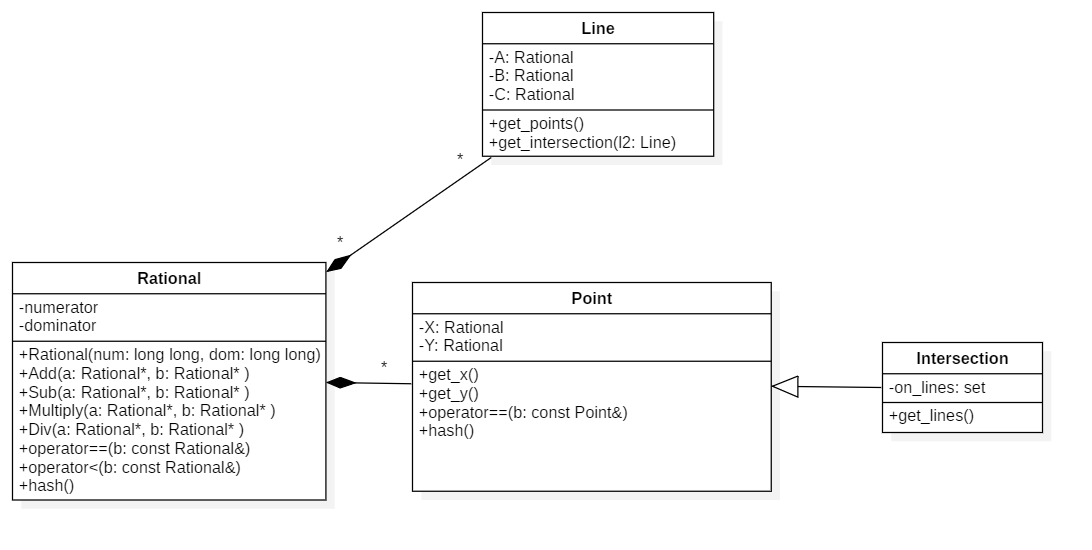
基于面向对象的思想,主要设计了有理数、点和线三个和平面几何有关的类,他们之间的联系见下图:
5 代码分析与性能分析
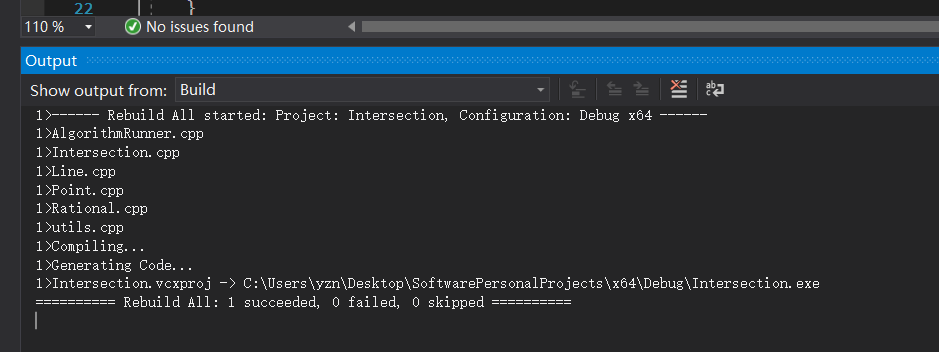
首先,使用Visual Studio自带的代码分析工具对所编写的代码进行了检查,得到没有issue发现的状态如下图所示:
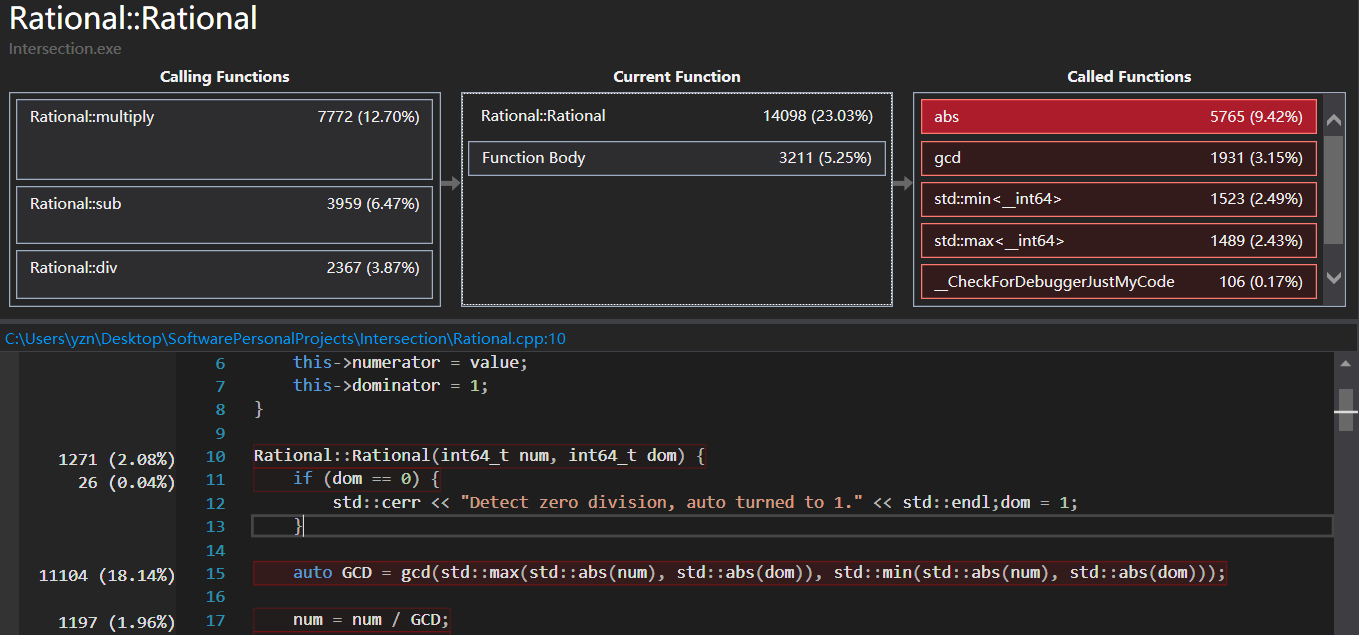
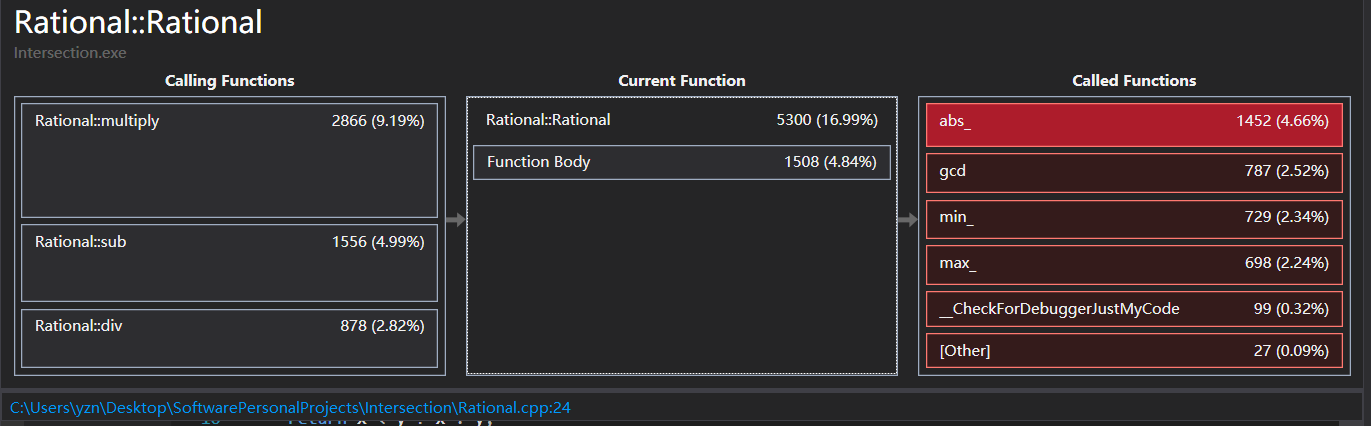
而后,使用了VS的性能分析工具,将所参与的直线数量调整至最大输入量N=500000,进行性能分析运行,运行60秒后中断分析结果,定位到目前的消耗最大的函数是Line 类的静态方法get_intersection(),再具体来说,是在生成交点时,自定义的Rational分数类之间的四则运算操作开销很大,具体来说有一下两个方面:
- 其一:是new operation的频次过多,造成过大的性能开销。关于这方面我在短时间内还未找到妥善处理的方法。
- 第二:是标准空间中所定义的abs, max, min函数性能开销很大,在这些函数进行人工inline重写后,函数的性能开销明显下降,如下图所示。
- 第三:GCD(求最大公因数)用于化简分数,也是一个性能开销大的函数,在改写其递归结构变为while循环类型后,性能开销存在些许下降,但并不明显。
6 代码说明
代码结构
对于实现的代码,可以按以下文件进行组织:
├─header
│ AlgorithmRunner.h
│ Line.h
│ Point.h
│ Rational.h
│ utils.h
│
└─source
│ AlgorithmRunner.cpp
│ Intersect.cpp
│ utils.cpp
└─geometry
Line.cpp
Point.cpp
Rational.cpp
项目基于面向对象的方式编写,在.h头文件中定义类的成员与方法,在每个.cpp文件中定义了类方法的具体实现。
下面我以编写的有理数(分数)和二维坐标点为例子,进行具体的代码说明:
- 成员与构造:有理数类中有两个成员,用于分别表示\(\frac{分子}{分母}\)的两个数字,两个数字属于不可更改的数据,在进行类初始化时即使用GCD(最大公因数)进行化简并保存。
- 运算:有理数类支持了加减乘除四种四则运算的方法,以满足在求解直线交点时所需要的所有运算。
- 重载方法:为了支持有理数能够使用STL容器,在此重载了部分操作符和hash函数,对于std::set类,需要重载小于操作符<,对于std::unordered_set类,需要重载hash函数和==操作符。
// 有理数类的实现
class Rational
{
private:
int64_t numerator;
int64_t dominator;
public:
Rational(int64_t value);
Rational(int64_t num, int64_t dom);
static Rational* add(Rational* a, Rational* b);
static Rational* sub(Rational* a, Rational* b);
static Rational* multiply(Rational* a, Rational* b);
static Rational* div(Rational* divee, Rational* diver);
bool operator==(const Rational& r);
bool operator<(const Rational& r);
size_t hash();
};
对于二维坐标点类,其用于表示用于确定直线的点和记录交点:
- 成员与构造函数:包括两个有理数用于表示x和y坐标。为了后续的扩展性,增加了线条的列表,表示该点存在于的线条对象中。
- 方法:Point类中所定义的主要方法是用于获取其内部成员变量的方法和其与Line类关系的维护。
- 重载方法:重载了==和hash函数,以支持部分STL容器。
class Point
{
private:
Rational* x;
Rational* y;
std::list<Line*> on_lines;
public:
Point(Rational* x, Rational* y);
Point(int64_t x, int64_t y);
void register_line(Line* l);
std::list<Line*>* get_lines();
Rational* get_x() const;
Rational* get_y() const;
bool operator==(const Point& p);
size_t hash();
};
代码单元测试
由于类方法封装得比较好,因此单元测试比较方便,以每个类为具体如下:
(补充)测试策略:
| 类 | 方法种类 | 测试逻辑 |
|---|---|---|
| Rational(有理数) | 生成方法 | 分数化简(分子分母分别为负零正) |
| 比较方法(==,<,hash) | @负零正三类数字中大小比较;未化简分数比较;@hash方法的正确性;hash碰撞;@指针和对象比较区分。 | |
| 运算方法 | 负零正数之间涉及四则运算;运算的交换律;零至少作为一个操作数;零作为结果。 | |
| Point(二维点) | 比较方法(<, ==) | 设计跨越四个象限的正方形四个点,自身、两两比较。 |
| 查询方法 | 查询正常情况;查询空值情况。 | |
| Line(直线) | 生成方法 | 投入相同坐标点的异常;两点排序正常检验。 |
| 交点求解 | 功能验证(相交、平行);变量边界溢出运算检验。 |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号