Machine Learning--线性回归(实例)
参考内容:
python数据挖掘与机器学习实战.方魏.机械工业出版社.2019.05
机器学习基础:从入门到求职.胡欢武.电子工业出版社.2019.03
回归分析是一种应用极为广泛的数量分析方法。它用于分析事物之间的统计关系,侧重考察变量之间的数量变化规律,并通过回归方程的形式描述和反映这种关系,以帮助人们准确把握变量受其他一个或多个变量影响的程度,进而为预测提供科学依据。在大数据分析中,回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析、时间序列模型,以及发现变量之间的因果关系。
一元线性回归分析
一元线性回归的概念
线性回归分析中,如果仅有一个自变量与一个因变量,且其关系大致上可用一条直线表示,则称之为简单线性回归分析。如果发现因变量Y和自变量X之间存在高度的正相关,则可以确定一条直线方程,使得所有的数据点尽可能接近这条拟合的直线。简单线性回归分析的模型可以用以下方程表示:Y=a+bx 其中,Y为因变量,a为截距,b为相关系数,x为自变量。
一元线性回归的实例
预测房屋价格: 一个简单的线性回归的例子就是房子价值预测问题。一般来说,房子越大,房屋的价值越高。于是可以推断出,房子的价值是与房屋面积有关的。这个案例中房子面积是自变量,房屋价格是因变量,因此,要预测房屋价格,就需要从给出的数据集中,找出符合Y=a+bx模型的线性方程。


# predict_house_price.py
# 1. 导入需要的包
from sklearn import datasets, linear_model
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# 2. 读取数据函数
def get_data(file_name):
data = pd.read_csv(file_name)
x_parmeter = []
y_parmeter = []
for single_square_feet, single_price_value in zip(data['square_feet'],data['price']):
# 遍历数据
x_parmeter.append([float(single_square_feet)])
y_parmeter.append([float(single_price_value)])
return x_parmeter, y_parmeter
# 3. 将数据拟合到线性模型
def linear_model_main(X_parameters,Y_parmeters,predict_value):
regr = linear_model.LinearRegression()
regr.fit(X_parameters,Y_parmeters)
# 训练模型
predict_outcome = regr.predict(predict_value)
predictions = {}
predictions['intercept'] = regr.intercept_
predictions['coefficient'] = regr.coef_
predictions['predicted_value'] = predict_outcome
return predictions
# 4. 绘制拟合曲线
def show_linear_line(X,Y):
regr = linear_model.LinearRegression()
regr.fit(X,Y)
plt.scatter(X,Y,color='blue')
plt.plot(X,regr.predict(X),color="red")
plt.xticks()
plt.yticks()
plt.show()
# 读取数据、进行预测
X, Y = get_data('E:/Data/6/input_data.csv')
show_linear_line(X,Y)
predictvalue = 700
result = linear_model_main(X,Y,predictvalue)
print("系数a:", result['intercept'])
print("系数b:", result['coefficient'])
print("预测价格:", result['predicted_value'])
系数a: [1771.80851064]
系数b: [[28.77659574]]
预测价格: [[21915.42553191]]
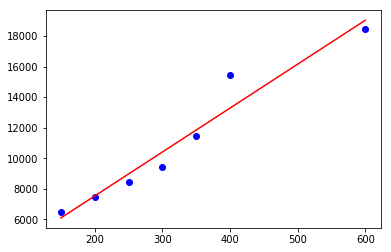
Intercept value(截距值)就是a的值,coefficientvalue(系数)就是b的值。得到预测的价格值为21915.4255——这意味着预测房子价格的工作做完了。为了验证数据是否拟合线性回归,所以需要写一个函数,输入为X_parameters和Y_parameters,画出数据拟合的直线。从图中可以看到直线基本可以拟合所有的数据点。
多元线性回归分析
多元线性回归的概念
多元线性回归分析是简单线性回归分析的推广,指的是多个因变量对多个自变量的回归分析。其中最常用的是只限于一个因变量但有多个自变量的情况,也叫多重回归分析。多重回归分析的一般形式如下:Y=a+b1X1+b2X2+b3X3+…+bkXk( 其中,a代表截距,b1,b2,b3…bk为回归系数。)
多远线性回归的实例
广告投入: 当结果值的影响因素有多个时,可以采用多元线性回归模型。例如,商品的销售额可能与电视广告投入、收音机广告投入和报纸广告投入有关系。故:
Sales=β0+β1TV+β2Radio+β3Newspaper

1. 读入数据
from sklearn import linear_model
import pandas
# 1.读入数据
data = pd.read_csv("E:/Data/6/Advertising.csv",header=0,index_col=0)
data
| TV | Radio | Newspaper | Sales | |
|---|---|---|---|---|
| 1 | 230.1 | 37.8 | 69.2 | 22.1 |
| 2 | 44.5 | 39.3 | 45.1 | 10.4 |
| 3 | 17.2 | 45.9 | 69.3 | 9.3 |
| 4 | 151.5 | 41.3 | 58.5 | 18.5 |
| 5 | 180.8 | 10.8 | 58.4 | 12.9 |
| ... | ... | ... | ... | ... |
| 196 | 38.2 | 3.7 | 13.8 | 7.6 |
| 197 | 94.2 | 4.9 | 8.1 | 9.7 |
| 198 | 177.0 | 9.3 | 6.4 | 12.8 |
| 199 | 283.6 | 42.0 | 66.2 | 25.5 |
| 200 | 232.1 | 8.6 | 8.7 | 13.4 |
200 rows × 4 columns
上面的数据具有如下特征:
- TV:在电视上投资的广告费用(以千万元为单位);
- Radio:在广播媒体上投资的广告费用;
- Newspaper:用于报纸媒体的广告费用;
- Sales:对应产品的销量。
在这个案例中,通过不同的广告投入,预测产品销量。因为相应变量是一个连续的值,所以这个问题是一个回归问题。数据集一共有200个观测值,每一组观测对应一个市场的情况。
2. 查看数据间的关系
# 2. 通过可视化各个特征和观测值的关系
import matplotlib.pyplot as plt
import seaborn as sns
sns.pairplot(data, x_vars=['TV','Radio','Newspaper'],y_vars=['Sales'],size=7,kind='reg')
plt.show()

从图中可以看出,TV特征和销量是有比较强的线性关系的,而Radio和Sales线性关系弱一些,Newspaper和Sales线性关系更弱。
3. 构建特征向量和标签
# 3. 使用pandas构建X(特征向量)和y(标签)
'''
scikit-learn要求X是一个特征矩阵,y是一个NumPy向量。pandas构建在NumPy之上。
因此,X可以是pandas的DataFrame,y可以是pandas的Series,scikit-learn可以理解这种结构。
'''
# 创建特征列表
feature_cols = ['TV','Radio','Newspaper']
# 使用列表选择原始DataFrame的子集,构建特征向量
X = data[feature_cols]
X = data[['TV','Radio','Newspaper']]
# 从DataFrame中选择一个Series
y = data['Sales']
y = data.Sales
X
| TV | Radio | Newspaper | |
|---|---|---|---|
| 1 | 230.1 | 37.8 | 69.2 |
| 2 | 44.5 | 39.3 | 45.1 |
| 3 | 17.2 | 45.9 | 69.3 |
| 4 | 151.5 | 41.3 | 58.5 |
| 5 | 180.8 | 10.8 | 58.4 |
| ... | ... | ... | ... |
| 196 | 38.2 | 3.7 | 13.8 |
| 197 | 94.2 | 4.9 | 8.1 |
| 198 | 177.0 | 9.3 | 6.4 |
| 199 | 283.6 | 42.0 | 66.2 |
| 200 | 232.1 | 8.6 | 8.7 |
200 rows × 3 columns
y
1 22.1
2 10.4
3 9.3
4 18.5
5 12.9
...
196 7.6
197 9.7
198 12.8
199 25.5
200 13.4
Name: Sales, Length: 200, dtype: float64
4. 构建训练集和测试集
构建训练集和测试集,分别保存在X_train、y_train、Xtest和y_test中。
# 4.构建训练集和测试集
# 使用交叉验证
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y) # 75% 用于训练 25%用于测试
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
(150, 3)
(150,)
(50, 3)
(50,)
5. 训练模型
使用sklearn做线性回归,首先导入相关的线性回归模型,然后做线性回归模拟。
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
# 训练模型
model = linreg.fit(X_train,y_train)
print(model)
print(linreg.intercept_) # 截距
print(linreg.coef_) # 系数
# 将特征名称和系数对应
zip(feature_cols,linreg.coef_)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
3.18324257719733
[0.04355291 0.19015449 0.00187221]
1
<zip at 0x1fcd01a5788>
对于给定了Radio和Newspaper的广告投入,如果在TV广告上每多投入1个单位,对应销量将增加0.04355个单位。也就是其他两个媒体的广告投入固定,在TV广告上每增加1000美元(因为单位是1000美元),销量将增加43.5(因为单位是1000)。同理,采用控制变量法,可分析其他两个变量。
6. 进行预测
通过线性模拟求出回归模型之后,可通过模型预测数据,通过predict函数即可求出预测结果。
y_pred = linreg.predict(X_test)
print(y_pred)
# 返回模型在测试集上的预测准确率
print("模型得分:",linreg.score(X_test,y_test))
[10.74391068 23.14564258 8.32679708 15.21951218 18.28945003 14.87833614
13.7803107 7.63132692 8.92202965 11.01760334 12.53937187 14.68253695
15.55290183 11.01469897 11.76553368 17.74441368 16.85875042 9.38817803
20.61167465 4.771148 10.76013573 18.12281809 17.31568335 15.00207018
16.24914813 8.14154239 18.41459647 21.86644162 21.18666811 16.48384668
24.61985703 21.02422026 11.4813219 20.97928742 13.30921663 7.2209075
15.33535201 7.60112899 12.52375857 16.99771224 12.79018816 11.62956032
20.72425247 17.31572264 11.89161417 6.34236115 20.1308101 10.79413639
17.74580942 9.98156724]
模型得分: 0.8631218575476306
7. 模型评估
对于分类问题,评价测度是准确率,但其不适用于回归问题,这里介绍3种常用的针对线性回归的评价测度。
- 平均绝对误差(Mean Absolute Error,MAE);
- 均方误差(Mean Squared Error,MSE);
- 均方根误差(Root Mean Squared Error,RMSE)。
# 此处采用RMSE
from sklearn import metrics
import numpy as np
sum_mean = 0
for i in range(len(y_pred)):
sum_mean += (y_pred[i] - y_test.values[i])**2
sum_error = np.sqrt(sum_mean / len(y_pred))
print("均方根为:", sum_error)
均方根为: 2.094615925156935
# 绘制预测和特测试集曲线
import matplotlib.pyplot as plt
def show_roc():
plt.figure()
plt.plot(range(len(y_pred)), y_pred,'b',label = "predict")
plt.plot(range(len(y_pred)), y_test,'r',label = "test")
plt.legend(loc="upper right")
plt.xlabel("The number of sales")
plt.ylabel("Value of sales")
plt.show()
show_roc()

小结
普通线性回归的介绍如上面所述,在 scikit-learn 中通过 linear_model.LinearRegression类进行了实现,下面总结一下该类的主要参数和方法。
- 参数
- fit_intercept:选择是否计算偏置常数b,默认是True,表示计算。
- normalize:选择在拟合数据前是否对其进行归一化,默认为False,表示不进行归一化。
- n_jobs:指定计算机并行工作时的 CPU 核数,默认是1。如果选择-1,则表示使用所有可用的CPU核。
- 属性
- coef_:用于输出线性回归模型的权重向量w。
- intercept_:用于输出线性回归模型的偏置常数b。
- 方法
- fit(X_train,y_train):在训练集(X_train,y_train)上训练模型。
- predict(X):用训练好的模型来预测待预测数据集X,返回数据为预测集对应的预测结果。
- score(X_test,y_test):返回模型在测试集(X_test, y_test)上的预测准确率,计算公式见下,score是一个小于1的值,也可能为负值,其值越大表示模型预测性能越好。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号