【3D数学基础：图形与游戏开发】笔记 第12章 几何图元

【3D数学基础：图形与游戏开发】笔记 第12章 几何图元

参考资料&原文链接

参考书籍：【3D数学基础：图形与游戏开发】 ISBN7-302-10946XTP.7262

(美) etcher Dun著、(美) an Arberry 清华大学出版社

GAMES101-现代计算机图形学入门-闫令琪

猎豹网校：游戏开发之3D数学基础

自由度

每个几何图元都有一个固有的属性：自由度。自由度是无歧义地描述该实体所需信息量的最小数目。
有趣的是，同一几何图元，不同表示方法所用到的自由度是不同的。然而，我们会发现“多余”的自由度
数量经常是由于图元参数化中的冗余造成的，这些冗余可以通过些适当的假设条件来消除，如假设向量为单位长度。

直线和射线

直线

• 直线向两个方向无限延伸。
• 线段是直线的有限部分，有两个端点。
• 射线是直线的“一半”，有一个起点并向一个方向无限延。

射线

在计算机科学和计算几何中，存在着这些定义的许多变种。本书使用“直线”和“线段”的经典定义但对“射线”的定义作出修改：

• 射线就是有向线段。

对我们来说，射线有起点和终点。这样，一条射线定义了一个位置，一个有限长度和一个方向(除射线长度为零)。任何射线都定义了包含这个射线的一条直线和线段。射线在计算儿何和图形学中占有非常重要的位置，这是本节讨论的重点。

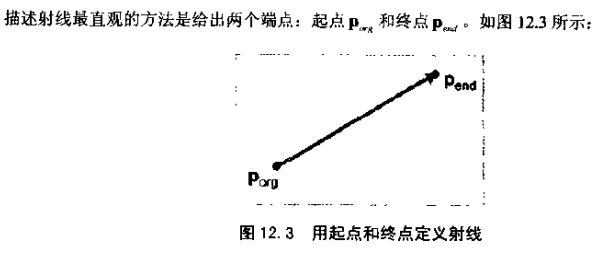
射线的表示

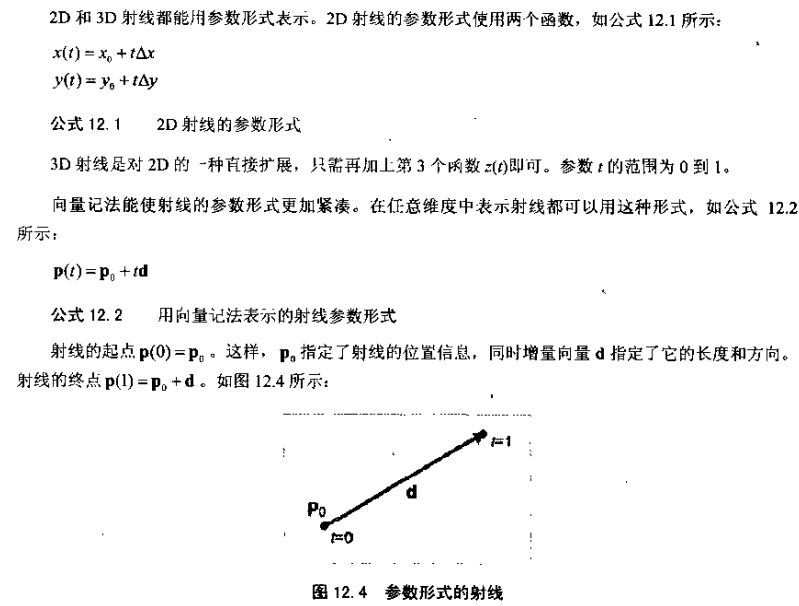
球和圆

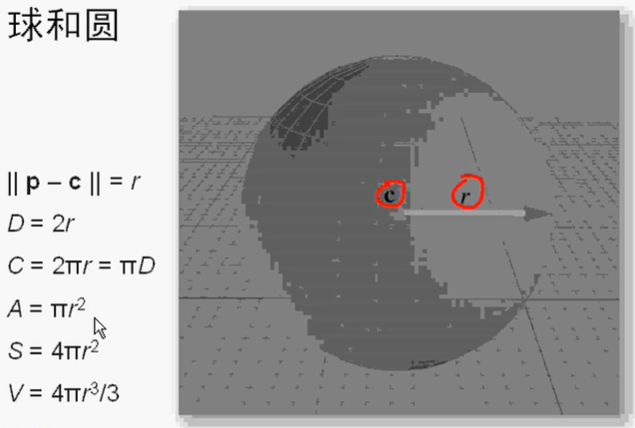
常用公式

• 向量c：圆心/球心。

• p：圆/球上一点。

• r：圆/球半径。

• D：圆/球直径。

• C：圆周长。

• A：圆面积。

• S：球表面积。

• V：球体积。

  圆面积的微积分是圆周长，球体积的微分是球表面积。

作用

球的简单性使它在计算几何和图形学中是几乎处不在。“边界球”经常用于相交性测试中，因为检验与一个球是否相交是非常简单的。而且由于旋转一个球时并不会改变它的形状，所以使用边界球时不必考虑物体的方向。

矩形边界框（AABB）

另一种常见的用来界定物体的几何图元是矩形边界框。矩形边界框可以是与轴对齐的或是任意方向的。轴对齐矩形边界框有一个限制，就是它的边必须垂直于坐标轴。缩写AABB常用来表示 axially aligned bounding box(轴对齐矩形边界框)，OBB用来表示 oriented bounding box(方向矩形边界框)。轴对齐矩形边界框不仅容易创建，而且易于使用。

AABB的表达

边界框大小

x_min<= x <= x_max

y_min<= y <= y_max

z_min<= z <= z_max

最大顶点和最小顶点

p_min = [x_min，y_min，z_min]

p_max = [x_max，y_max，z_max]

中心点

中心点c = (p_min + p_max)/2

尺寸向量

尺寸向量s是从p_min指向p_max的向量，包含了矩形边界框的长，宽，高：

s = p_max - p_min

半径向量

半径向量r是从中心点指向p_max的向量：

r = p_max - c

= s / 2

明确地定义一个AABB只需要p_min，p_max。，c，s，r这5个向量中的两个(除s和r不能配对外，它们中的任意两个都可配对)。在一些情况下，某些配对形式比其他的会更有用。我们建议用p_min，和_max。表示一个边界框，因为实际应用中，使用它们的频率远高于c，s，r。当然，由p_min，和_max计算其余三个中的任意一个都是很容易的。

AABB与边界球

很多情况下，AABB比边界球更适合于做定界体。

• 计算一个点集的AABB，在编程上更容易实现，并能在较短的时间内完成。计算边界球则困
  难得多。
• 球体一般比AABB要大。对实际世界里的许多物体，AABB提供了一种“更紧凑”的边界。当然，对于某些物体，边界球更好(设想一个本身就是球形的物体!)。在极端的情况下，AABB的体积可能仅相当于边界球体积二分之一，大部分时候边界球的体积会比矩形边界框的体积大得多，比较一下电线杆的边界球和AABB就知道了，图12.11所示为不同物体的AABB与边界球的比较。

边界球的根本问题是它的形状只有一个自由度——半径。而AABB却有三个自由度——长、宽、高。因此，它可以调节这些自由度以适应不同物体。对图12.11中的大部分物体除了右上角的星形体外，AABB都比边界球小。对这颗星，边界球也仅比AABB略微小一些。通过图12.11，我们可以注意到AABB对物体的方向很敏感。比较下面两枝枪的AABB。图中枪的大小都是相同的，只是方向不同而已;还应注意到在这一情况下边界球大小相同，因为边界球对物体方向不敏感。

AABB变换

当物体在虚拟世界中移动时，它的AABB也需要随之移动。此时我们有两个选择用变换后的物体来重新计算AABB，或者对AABB做和物体同样的变换。所得到的结果不一定是轴对齐的(如果物体旋转)，也不一定是盒状的(如果物体发生了扭曲)。不过，通过“变换后的AABB”进行计算要比通过“经过变换的物体”计算AABB快得多，因为AABB只有8个顶点。

根据变换的不同，这种方法可能使新边界框比原边界框大许多。例如，在2D中，45°的旋转会大大增加边界框的尺寸。如图 所示。

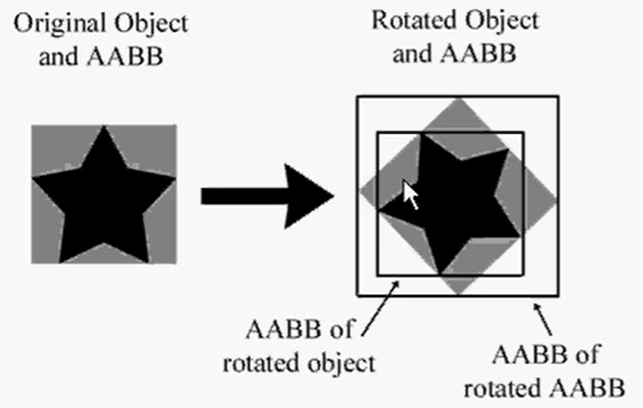
通过“变换后的AABB“计算不能只是简单地变换8个顶点，也不能通过转换原p_max和p_min来得到新的p_max和p_min——这样可能会导致x_min>x_max、为了计算新的AABB，必须先变换8个顶点，再从这8个顶点中计算一个新的AABB，计算的方式是：

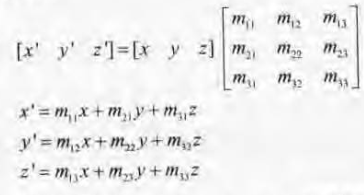
[x^'，y^'，z^']是原边界框，m那一坨是旋转矩阵，[x，y，z]代表一个点，而AABB有8个点，就要用这8个点分别和旋转矩阵相乘，然后在再其中找出最大的和最小的。

这样显然太慢了，可以用一点技巧，例如我现在要找出m₁₁x+m₂₁y+m₃₁z最小的，那么我可以：

• 若m > 0，则我用一个最小的x_min代入计算。
• 若m < 0，则我用一个最大的x_max代入计算。

这样就能够最小化乘积。

计算最大值则与之相反。

平面

隐式定义

在3D中，平面是到两个点的距离相等的点的集合。平面完全是平的，没有厚度，且无限延伸。

例如：在点r和点q之间有一个平面，平面上有任意一点p，p到r和p到q的距离是相等的：

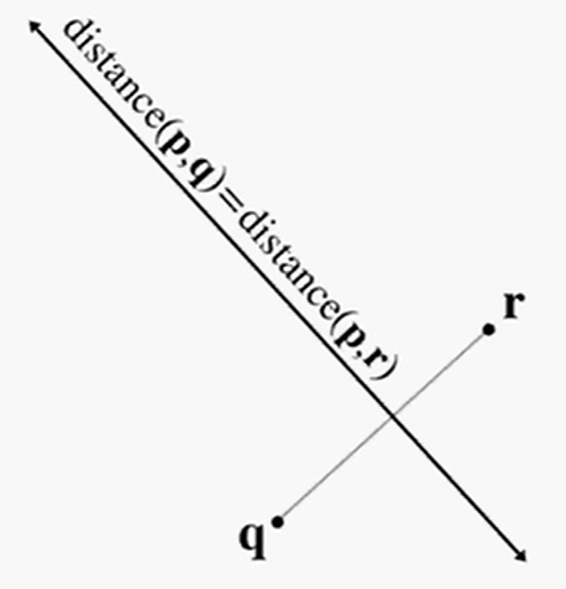
平面方程：

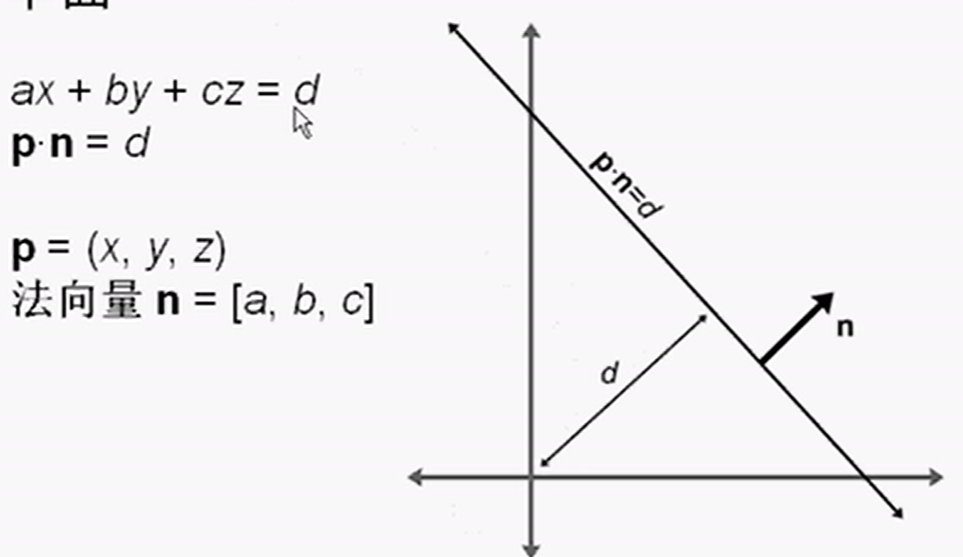
ax + by + cz = d ：平面方程。

p：平面上任意一点。

d：原点到平面的距离。

n：法向量。

它们有如下关系：

• p · n = d

• n · p = d

• n · q = d

• n · p = n · q

• n· ( p - q ) = 0

  这一行的几何意义就是a垂直于从q到p的向量参考点乘的几何意义)。这对于平面上的任意p，q点都是成立的。因此，n垂直于平面上的任意向量。

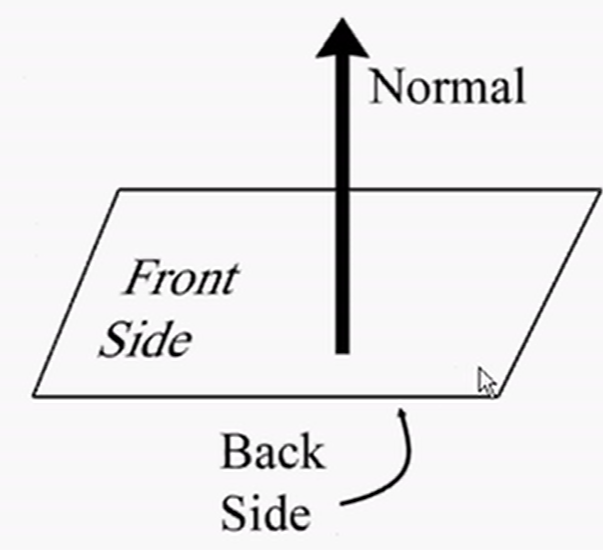
平面的正面和背面

我们还假设平面有“正面”和“反面”一般来说，法向量n指向的方向是平面的正面( Front side)。

用三个点来定义

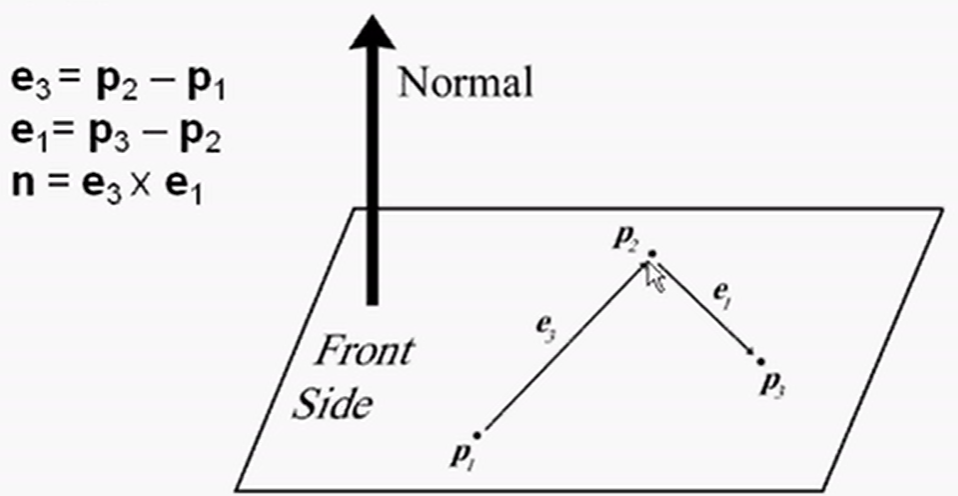
左手坐标系。

点到平面的距离

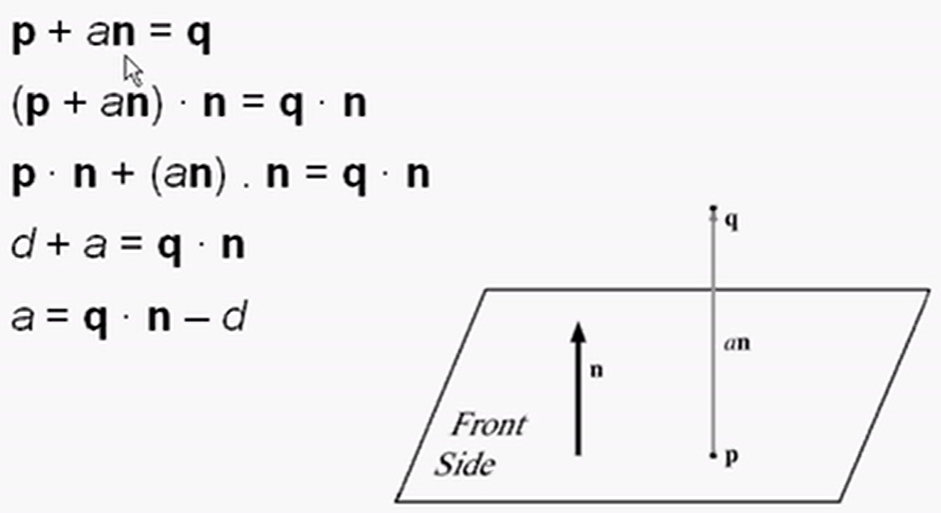
不在平面的一点q，与在平面上的一点p的最短距离很明显就是q垂直于平面的距离，我们将法向量n看做单位向量，给单位向量乘以a倍再加上p点就等于q点，即：q + an = q。推导公式比较简单，看图即可。注意前面推导的：p · n = d。

三角形

角形在建模和图形学中有着极其重要的位置。复杂3D物体的表面，如车或人体，都是用三角形模拟的。像这样一组相连的三角形称作三角网格第14章将详细讨论这一主题。在学习怎样操作多个角形之前，先要学会如何操作单个三角形。

角形是通过列出它的三个顶点来定义的。这些点的顺序是非常重要的，在左手坐标系中，当从三角形“正面”看时，经常以顺时针方向列出这些点。设这三个顶点为v₁，v₂，v₃。

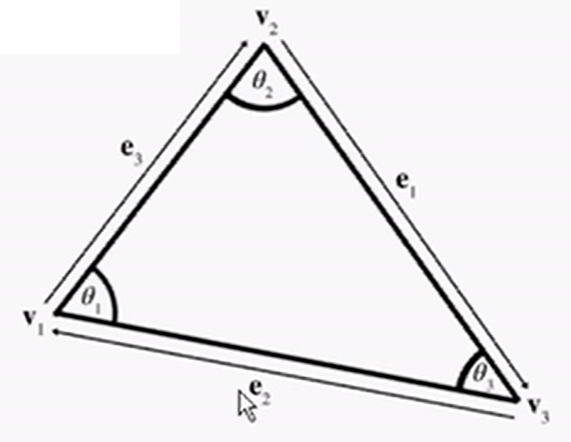
基本关系

设l_t为e_t的长度。注意e_t，、l_t和v_t的对应关系，v_t为相应下标的顶点，它们的关系如下;

e₁ = v₃ - v₂ l₁ = ||e₁||

e₂ = v₁ - v₃ l₂ = ||e₂||

e₃ = v₂ - v₁ l₁ = ||e₃||

正余弦公式

三角形周长

p = l₁ + l₂ + l₃

三角形面积

用平行四边形计算面积

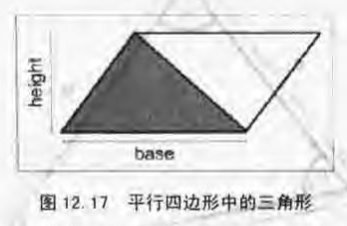
A = bh/2

用海伦公式计算三角形面积

如果不知道高，可以使用海伦公式计算面积，它只需要提供三边的长度即可。设s为周长的一半(也称作半周长)，如公式12.19所示：

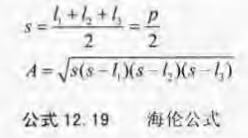
海伦公式非常有用，因为它在3D中使用非常方便。

在2D中用坐标计算三角形面积

有时候，高和周长都没有直接提供，所知道的只有顶点的笛卡尔坐标。(当然，总是可以从坐标中算出边长，但在某些情况下，我们想要避免这种代价相对较高的计算。)

A = [(y₁ - y₃)(x₂ - x₃) + (y₂ - y₃)(x₃ - x₁)] / 2

在3D中用叉乘计算三角形面积

在3D中，通过叉乘来计算三角形的面积。两向量a，b叉乘的大小等于以a，b为两边的平行四边形的面积。因为三角形面积等于包围它的平行四边形的一半，所以我们有了一种简便方法。给出三角形的两个边向量，e₁和e₂，则三角形面积为：

A = ||e₁ × e₁|| / 2

三角形的特殊点

重心

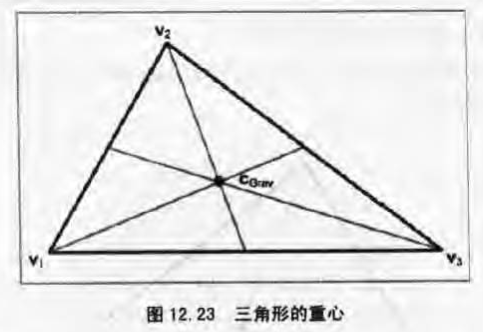
重心是三角形的最佳平衡点，它是三角形三条中线的交点(中线指从顶点到对边中点的连线)图12.23展示了一个三角形的重心。重心是三个顶点的几何均值：

重心也被称作质心。

内心

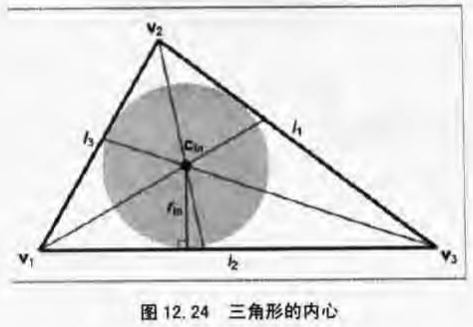
内心是指到三角形各边距离相等的点。之所以称作内心是因为它是三角形内切圆的圆心。内心是角平
分线的交点，如图12.24所示。

内切圆解决了寻找与三条直线相切的圆的问题。

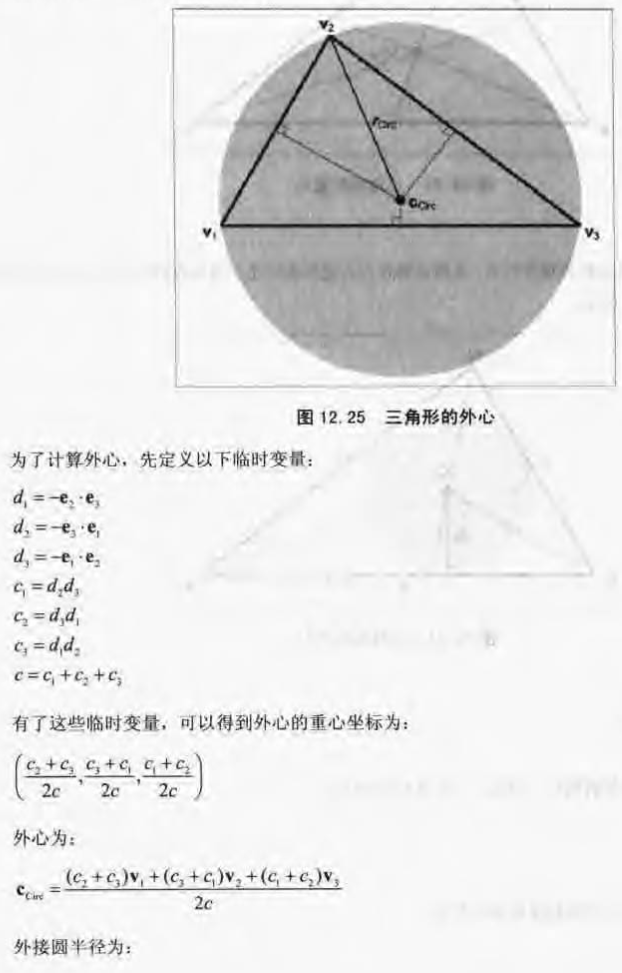
外心

外心是三角形中到各顶点距离相等的点，它是三角形外接圆的圆心。外心是各边垂直平分线的交点。
图12.25展示了一个三角形的外心。

多边形

简单多边形和复杂多边形

简单多边形不包含“洞”复杂多边形可能包含“洞”(图12.26)。简单多边形可以通过沿多边形列出所有顶点来描述(左手坐标系中，通常以从多边形正面看时的顺时针方向列出所有点)。简单多边形的使用频率比复杂多边形高得多。

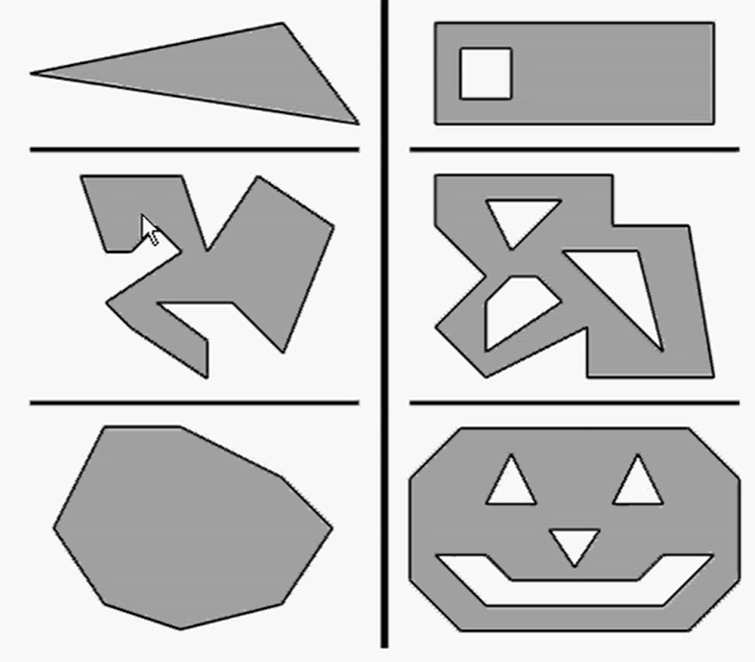
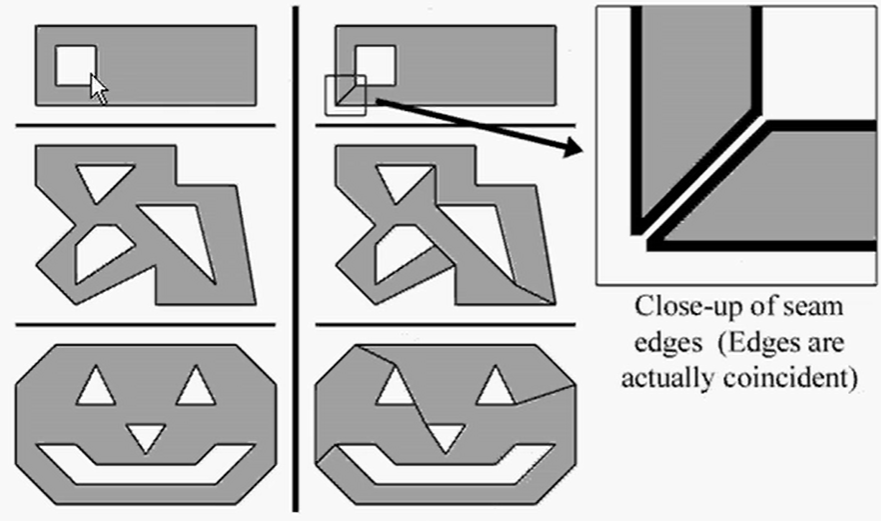
通过添加一对“接缝”边，能将任意复杂多边形转化成简单多边形，如图12.27所示。见右边的放大图，我们在每个“缝”添加了两个边。这两个边实际上是重合的，放大图中将其分开是为了让您看得更清楚。当我们考虑到绕多边形的边的顺序时，这两个接缝边的方向是相反的：

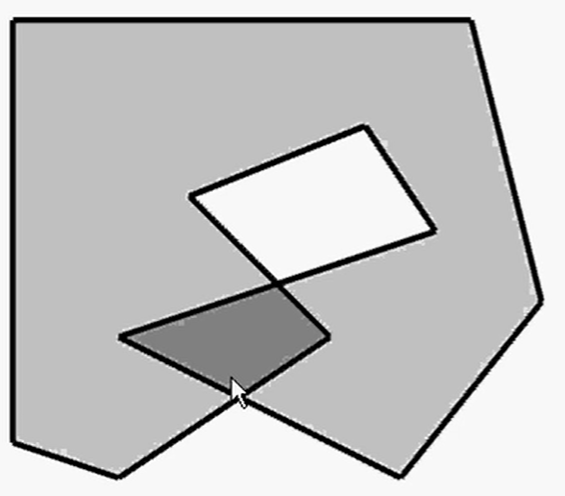
自相交多边形

大多数简单多边形的边不相交。如果有的边相交了，那么这个多边形叫作自相交多边形。一个简单的
自相交多边形如图12.28所示：

我们大多数时候与非自相交多边形打交道。

凸多边形和凹多边形

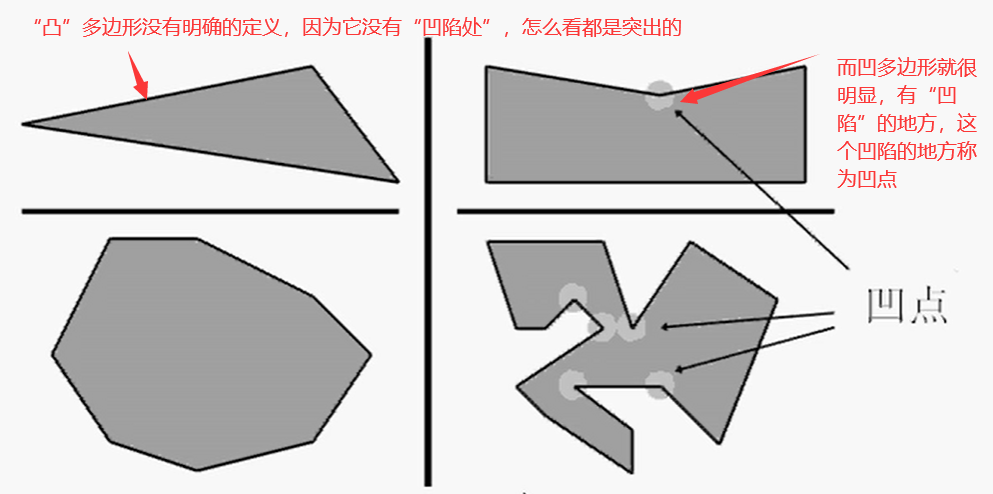
多边形的基本性质

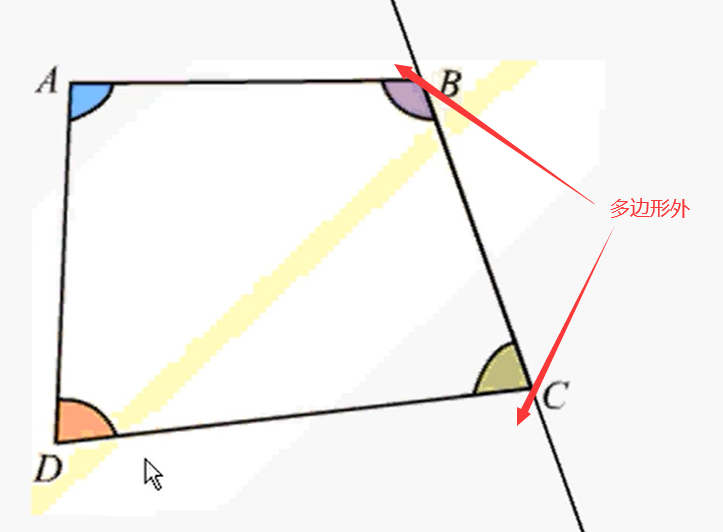
多边形有内角，内角和 = （n - 2）× 180°，其中n为多边形的边数。例如三角形的内角和就是180°。

判断多边形是凹多边形还是凸多边形：

对于一个凸多边形，内角不会大于外角。

所以，将外角和与内角和进行比较，选取其中较小的角和：

• 若角和 = （n - 2）× 180°，则为凸多边形。
• 若角和 < （n - 2）× 180°，则为凹多边形。

三角分解和扇形分解

任意多边形都能分解为三角形。因此，所有对三角形的操作都能应用到多边形上。复杂、白相交、甚至简单的叫多边形的分解都不是件简单的工作，稍微超出了本书的范围。
幸运的是，简单多边形的三角分解是一件容易的事。一种显而易见的三角分解技术是选取一个点(称
作第一个点)，沿着顶点按“扇形”分解多边形。给定一个有n个顶点的多边形，沿多边形列顶点v₁…v_n
能够很容易地构造形如{v₁，v_i-1，v_i}的n-2个三角形，见图12.30。

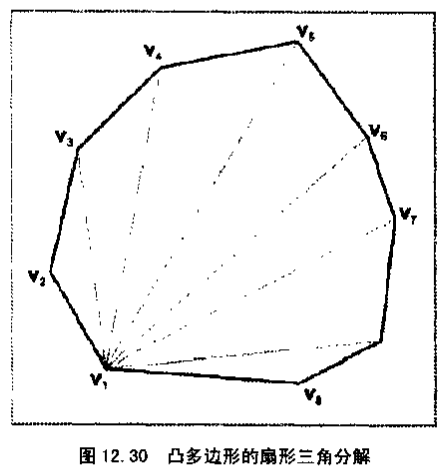
扇形三角分割会分割出一些长的，较细的三角形，这在某些情况下会引起麻烦。如同计算表面的法向量一样，数值的不精确性在度量极小的角时会造成一些问题。

一种更加“聪明”的分解方法是：连接两顶点的对角线将一个多边形分解为两部分。这时，对角线端
点处的两个内角都能分解为两个新的内角。因此，总共产生了四个新内角。为了分解多边形，选择能使这四个新内角中最小的角最大化的对角线，用这条对角线将多边形分为两个。对分割后的每一部分都递归应用这个过程直到剩下的都是三角形。

这个方法产生较少的细三角形。但是在实践中，它过于复杂。根据几何学和应用目的，扇形分解已经
足够了(并且简单得多)。

本文标签

游戏开发、3D数学基础：图形与游戏开发、Unreal Engine、游戏开发基础、数学、游戏开发数学基础、书籍笔记、笔记。