【GAMES101-现代计算机图形学入门-闫令琪】笔记 Lecture 04 Transformation Cont

【GAMES101-现代计算机图形学入门-闫令琪】笔记 Lecture 04 Transformation Cont

参考资料&原文链接

GAMES101-现代计算机图形学入门-闫令琪

猎豹网校：游戏开发之3D数学基础

上节课

前面21分钟是复习：

后面才是正片：

证明：R_-θ = R_θ^-1

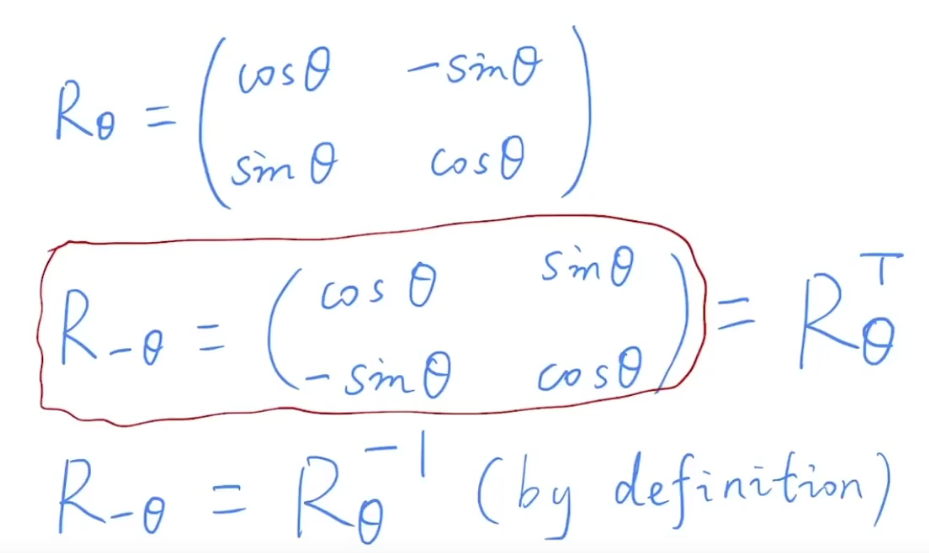
3D Transformations

这部分和【3D数学基础：图形与游戏开发】笔记 第10章 3D中的方位与角位移内容相同，不再赘述，如果需要了解可以点击前往笔记并点击这里前往原视频，看着视频对照笔记食用体验更佳。

Viewing(观测) transformation

把三维空间中的一个物体变成一张照片显示到屏幕上。即3D->2D。

引入：如何拍摄一张照片？

• 找到场景，放上人。（模型变换，Model Transformation）

• 找个好的角度、位置放上摄像机（视图变换，View Transformation）

• Cheese！（投影变换，Projection Transformation）

  以上三个变换简称为MVP变换。

View(视图)和Model(模型变换)

视图变换：变换相机的角度和位置。

模型变换：变换物体的角度和位置。

这两个变换，都会影响最终图形中，物体的位置，角度。而这两个变换，可以达到相同的效果。比如，你想要一个倒着的水杯图形，可以把你自己倒立，这样看到的水杯就是倒立的了。或者把水杯倒立，自己直立，也能看到倒立的水杯。

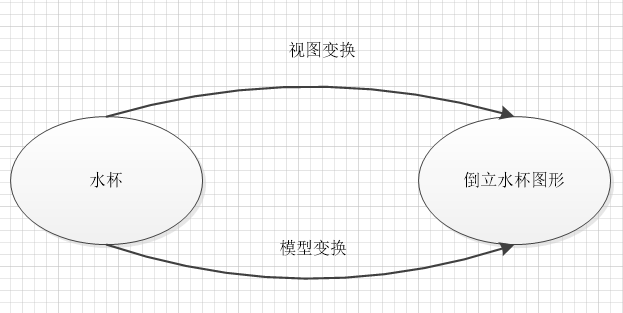
如图所示，这两种变换，可以看做达到目的的不同途径。甚至可以同时使用视图变换和模型变换，只要最终拿到了我们想要的图像就可以了。至于使用的是视图变换，还是模型变换，看我们理解问题的角度。

不论是模型变换还是视图变换，都是把物体按照视图变换的矩阵做一次变换，也就是和相机一起变换，所以这两个变换做的事情都差不多，大家习惯将它们放到一起成为模型/视图变换。

View(视图)/ Camera transformation

如何定义一个相机

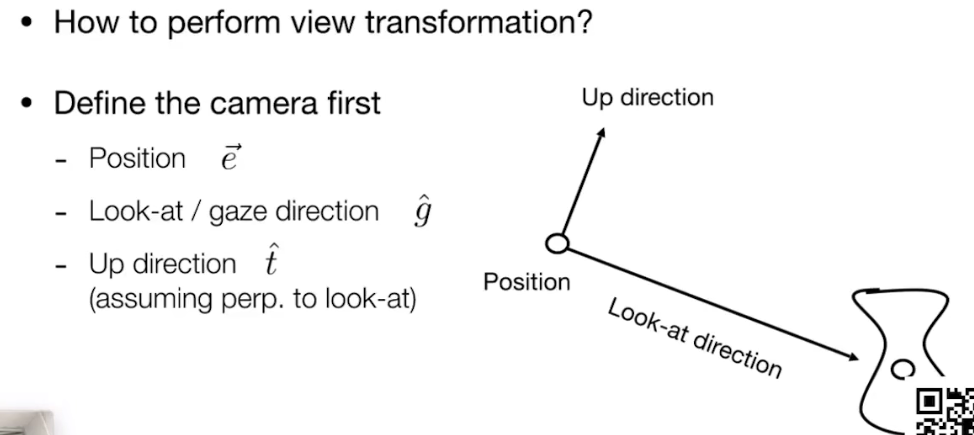
需要：

• 相机的位置。用向量e来表示。
• 相机往哪看。用向量g来表示。
• 相机的向上方向。如果相机旋转45°，拍出来的照片就是斜的。用向量t来表示。

如何进行视图变换

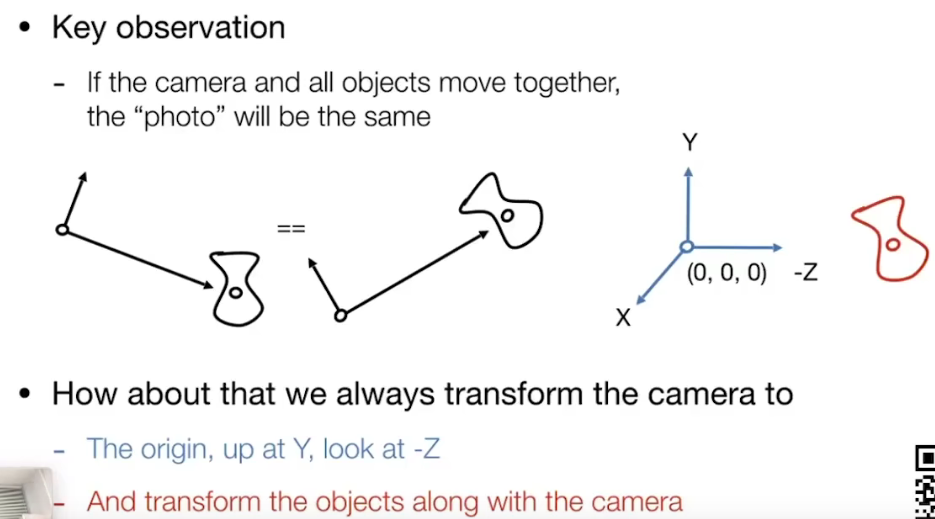
• 将相机从在3D中的某一个点移动到原点，即从世界坐标系变换到摄像机坐标系。向上方向是Y轴，看向-Z轴。（约定俗成）即像这样：

  

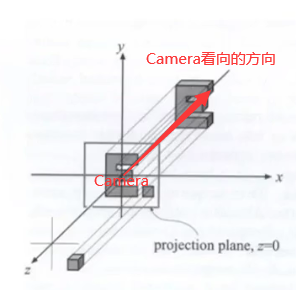
• 其他物体相对着相机一起移动（这样就能保证拍出来的照片和相机移动到原点之前的照片一样）。

从模型到相机

用矩阵如何表示

解释：

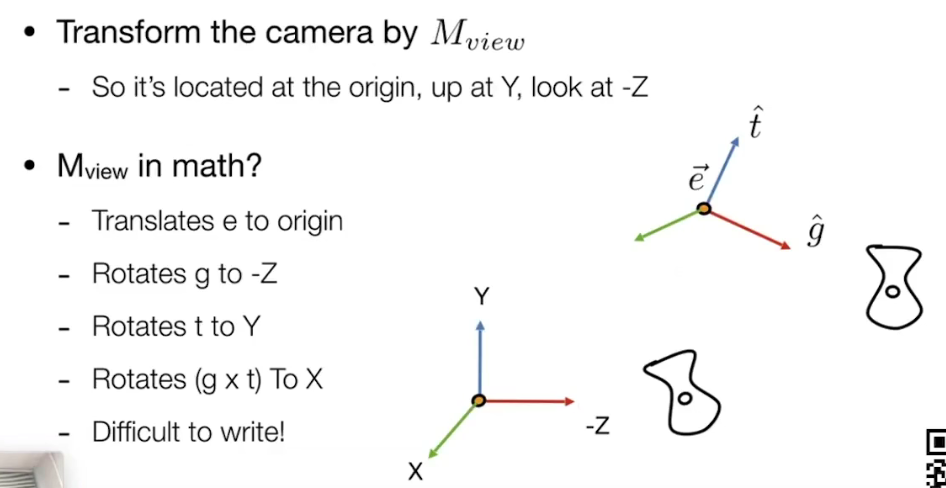
• 写出M_view（模型视图）的矩阵。M_view = R_view（旋转矩阵）T_view（平移矩阵）。

  注意这里是先平移再旋转，所以T_view是写到后面的。并且相机已经移到了原点。

• 平移向量e到原点。然后写出T_view的矩阵：

  

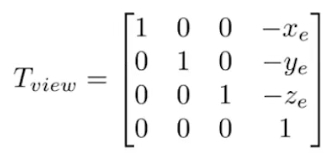
  注意：前面说过最后一列是用来表示平移的。从原来3D中的点要平移到原点自然是加上对应坐标的负数。

• 旋转向量g到-Z轴，向量t到Y轴。最后用 g × t 得到 X轴（右向向量）。

  你要把任意的一个轴旋转到规范化的一个轴上，这个旋转不好写（例如g->-Z轴（0,0,-1），g旋转了其他的轴也要跟着旋转）。后面的t旋转到Y轴也不好写。

• 所以现在反向思考。直接写不好写，但是反过来写好写。就像是e、g、t不动，反过来把X、Y、Z轴旋转到它们对应的轴上。

  即X（1,0,0）-> ( g × t)、 Y(0,1,0) -> t、Z(0,0,1) -> -g。

  即先求它们的逆变换矩阵，再求原始变换矩阵。

• 如何变换？

  先把相机的右、上、前向量放到矩阵里面，然后由于我们要旋转，前面学过齐次矩阵，所以扩充一列一行，得到的矩阵如下：

  

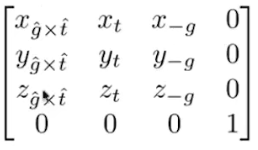
  我们将这个矩阵分别与X（1,0,0,0）^T相乘得到的就是第一列。

  同理，与Y（0,1,0,0）^T相乘得到的就是第二列，与Z（0,0,1,0）^T相乘的到的就是第三列。

  还记的前面写过的一个矩阵吗？它给我们的结论是：

  正交矩阵的转置矩阵等于其逆矩阵。即：R^T = R ^-1。所以我们就得到了：

  

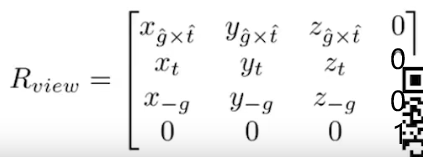
Projection(投影) transformation

正交投影和透视投影的区别

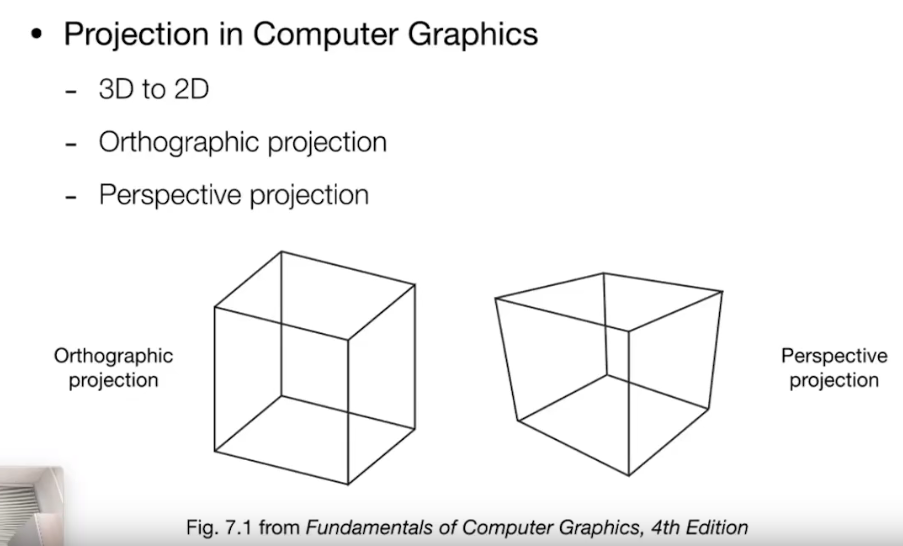
正交投影：投影后平行线仍然是平行线。

透视投影：投影后平行线会相交，即人眼视觉：近大远小。

这个例子有点抽象，下面这个会直观一点：

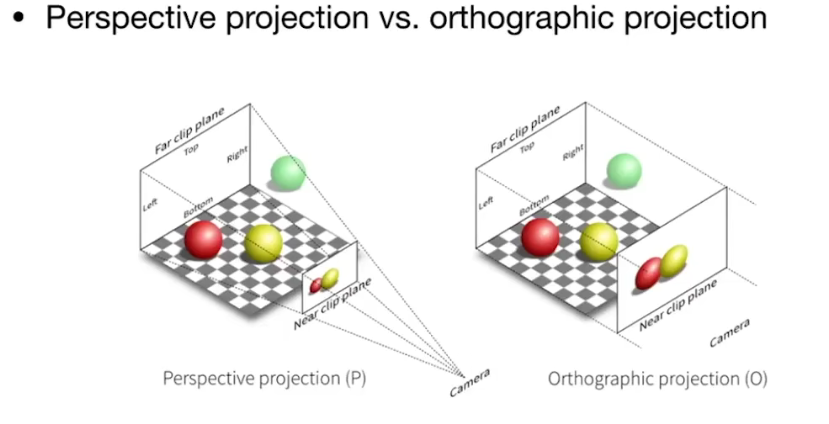
如何用数学来表示他们

透视投影：给定一个点（Camera）的位置，从点发出延伸出来的四棱锥到一个近平面上，我们希望把近平面上的东西全部都能显示出来。

正交投影：假设相机无限远，近平面投影出来Camera看到的东西都是一样大。

Orthographic(正交) projection

简单做法

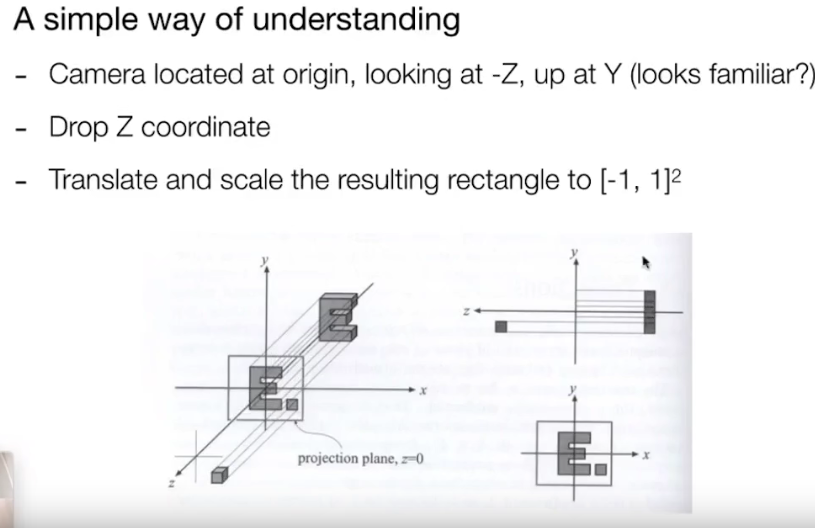
左边那副图：

• 摄像机的+Z轴的小方块和-Z轴的字母“E”是一个在“前”一个在“后”。中间那个就是正交投影的正视图，你会发现就是一个平面，因为我们把Z轴丢弃了。
• 这样的话都是在一个平面，你就还会发现一个问题，如何区分物体在投影前是在前还是在后呢？后面再解决。

右上那副图：是正交投影的侧视图。

右下那副图：是正交投影的结果图，不管右上那副图的坐标是多少，我们都将物体的坐标移到[-1,1]²这个范围，这是一个约定俗成的一个做法，因为方便计算。

正规做法

这个做法并不是很方便，现在介绍一个正规一点的做法：

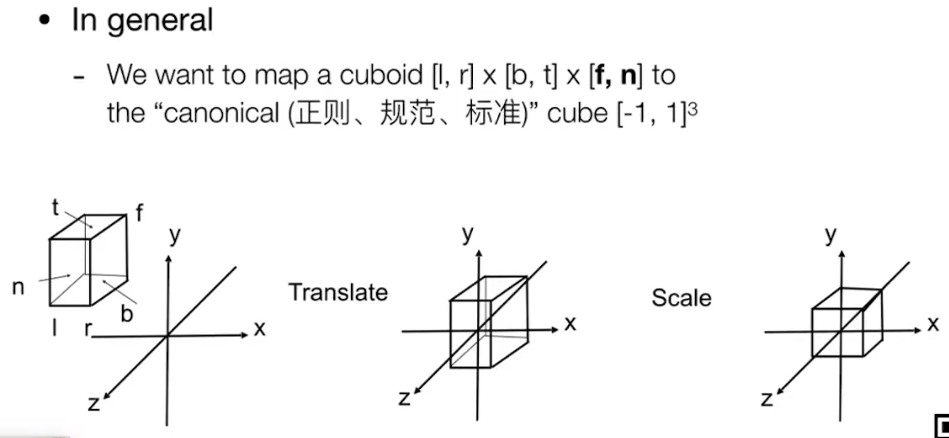
左方那个图：定义了一个空间中的立方体，其中（left，简写为l）l、r（right，简写为r）是点，n（near，近面）、b（button，底面）、t（top，上面）、f（far，远面）是面。我们只需要保证它的中心在原点、左右在X轴上，上下在Y轴上，远近在Z轴上。并且它的长宽不变，得到中间那副图。

右方那个图：将中间那副图再尝试将它的长宽映射到一个标准[-1,1]³的范围内，得到一个标准的立方体。

正规做法与简单做法不一样的地方在于：简单做法直接把Z轴丢掉了，而正规做法是先平移再缩放：

写出它的矩阵表示

注意：

• 因为我们是向-Z看，所以近>远。即物体如果离我们越远Z值就应该越小，物体如果离我们越近则Z值就应该越大，即（n > f）。
• OpenGL是左手坐标系，在API的调用上会有一些方便，但也是会产生一些问题（例如 X × Y != Z）。
• 在变换完之后物体的长宽高会拉伸，这时候先不做处理，等后面视口变换还要拉伸一次，那个时候再一起处理。

Perspective(透视) projection

透视投影概述

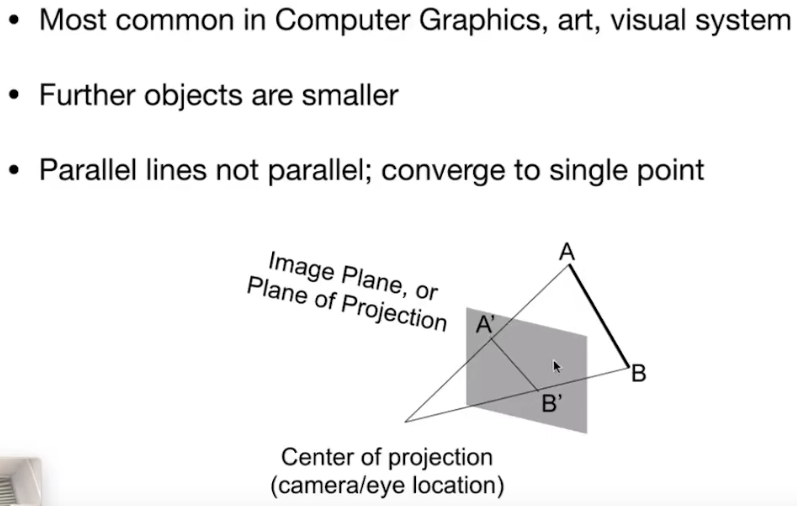
• 透视投影是在视觉系统中用的最多的投影。
• 透视投影即是近大远小。
• 透视投影后的平行线不再平行，仔细查看图中原线段AB和透视投影后的A^'B^'。

是欧几里得错了吗

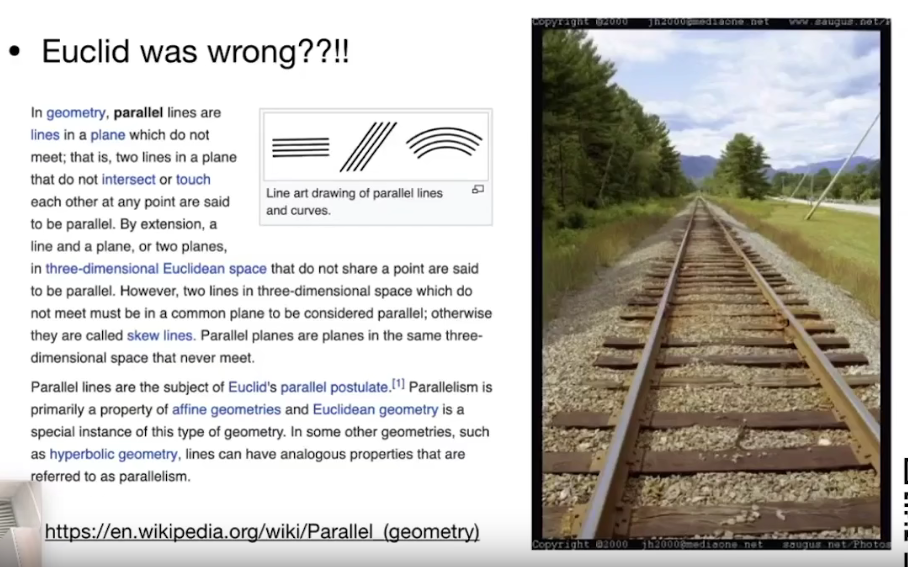
欧几里得说平行线永远都是平行线，永不相交。但是在照片中看到了平行线是在远处相交了的，是他错了吗？

并不是，欧几里得是说的一个平面，而透视投影是一个平面投影到另一个平面，所以投影的结果发生了变化，实际上原平面的平行线还是平行线，只不过我们观测的是投影后的平面，所以误以为平行线相交了。

在继续进行之前

前面说了齐次坐标只要同乘一个不为零的系数，表示的坐标都不会改变：

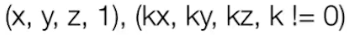
那我乘谁不是乘呢，干脆我们同乘一个Z，就变成了这样：

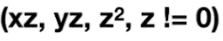
比如（1,0,0,1）和（2,0,0,2）都表示同一个点：（1,0,0）。这个东西简单但是有用。

如何理解透视投影

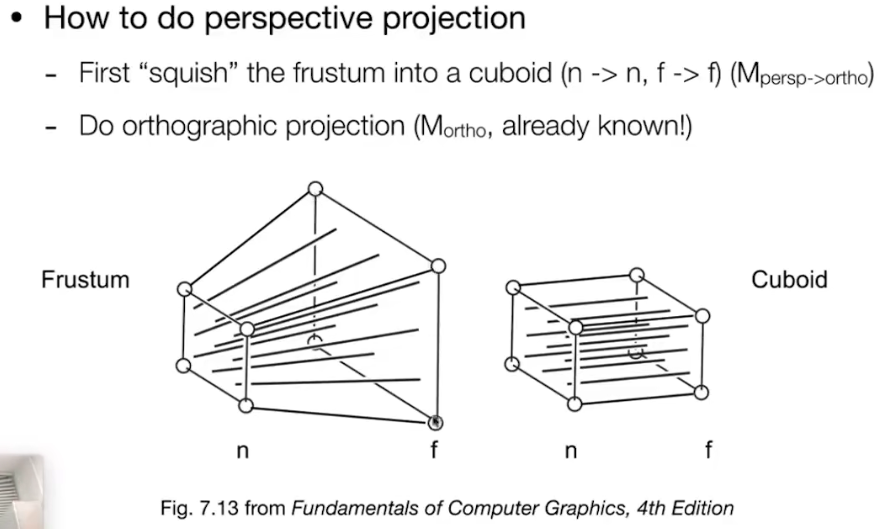
• 透视投影和正交投影都有两个面，一个前（n）一个后（f），所以我们可以首先将截锥“挤压”成长方体(n -> n, f -> f) ，即M_persp->M_ortho。
• 然后再做正交投影。透视投影里面的线和正交投影里面的线是一样的，只不过一个是面对面（棱台），一个是点对面投影（长方体）。

透视投影的矩阵可以直接写出来，但是不好理解。

如何“挤”

“挤”的过程有几个规定：

• 近平面（n面）和近平面上的点永远不变。
• 远平面（f面）“挤”完之后Z值不变。
• 远平面（f面）“挤”完之后中心点不变。

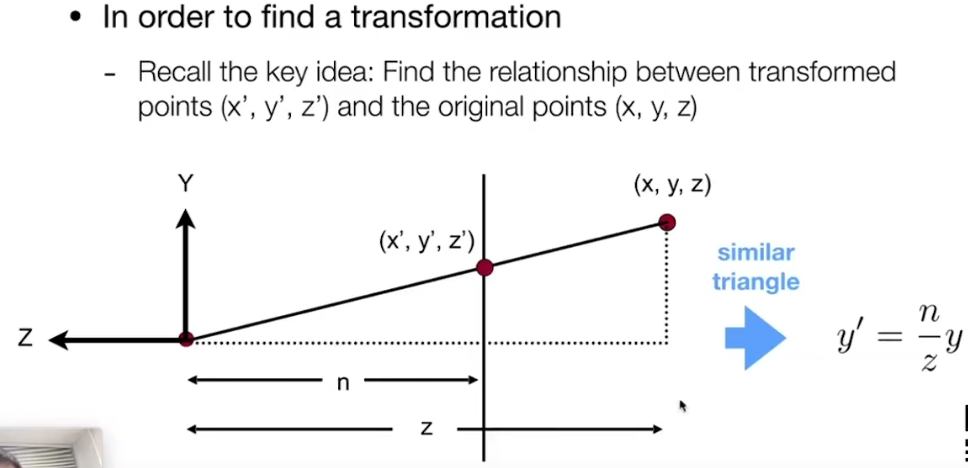
注意Camera的位置是在原点。原来的点(x,y,z)和新的点(x^',y^',z^')在Y轴上延伸到Camera的位置，它们构成了一个相似三角形。由相似三角形的对应角相等，对应边成比例可以计算出新的点的位置(x^',y^',z^')。

这里是Y，同理对于X也是一样的。所以任意在f面找到一点(x,y,z)就能都能找到在n面“挤”过来的新点(x^',y^',z^')。

写出矩阵

现在有了“挤压”（persp -> ortho）的齐次矩阵：

能否通过它来反推出M_persp->ortho^(4×4)矩阵呢？

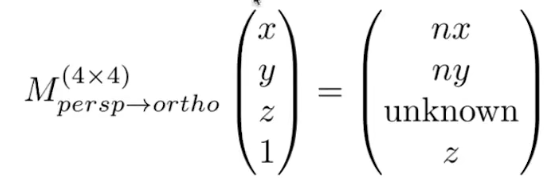
答案是可以，通过M_persp->ortho · [x,y,z,1]^T的结果（即“挤压”的齐次矩阵）可以大概推算出M_persp->ortho^(4×4)：

现在我们只差第三行，如何求出第三行，能在M_persp->ortho 矩阵中找到什么信息吗？

注意最后两句话是解题的关键，可以使用待定系数法解除这几个数。

利用第一点：近平面上的任何点都不会改变。

所以可以将原来的[x,y,z,1]^T中的z换成n，得到：[x,y,n,1]^T，再同乘以n，就得到了[nx,ny,n²,n]^T。

即某一个矩阵 × [x,y,n,1]^T = n² (这里明显的可以看出n²和x、y没有任何关系)。

最后由上式一样的反推：由结果 = n²就能反推出来这个矩阵 =（0,0,A,B）。其中A、B还不能确定，它存在以下两种情况：

• 若A=0， 0 * n = 0。这时B可以等于n²。
• 若A=n，n * n =n²。这时B可以等于0。

再利用第二点：远平面上的任意z点都不会改变。

找到屏幕特殊点，即屏幕中心点，利用它的性质：

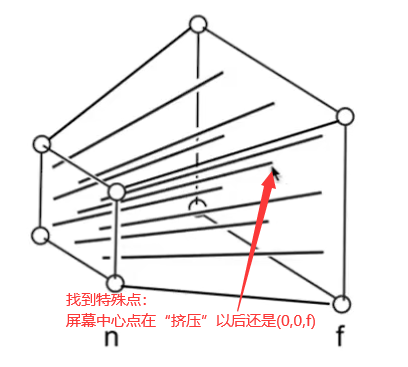
再求解：

联立方程组就能解出来：

现在已经得到了M_persp->ortho，只需要再做一次正交投影即可。最后透视投影的矩阵M_persp = M_orthoM_persp->ortho。

本文标签

计算机图形学、游戏开发、GAMES101-现代计算机图形学入门-闫令琪、Unreal Engine、游戏开发基础、视频系列笔记、笔记。