【3D数学基础:图形与游戏开发】笔记 第14章 三角网格
【3D数学基础:图形与游戏开发】笔记 第14章 三角网格
参考资料&原文链接
参考书籍:【3D数学基础:图形与游戏开发】 ISBN7-302-10946XTP.7262
(美) etcher Dun著、(美) an Arberry 清华大学出版社
网格
网格就是由很多个三角形或者多边形构成的,在图形学和建模中广泛应用,用来模拟复杂物体的表面。三角形网格:
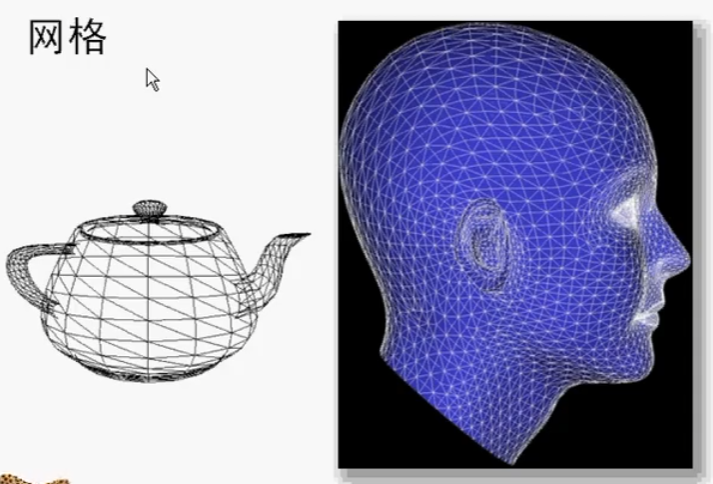
四边形网格:
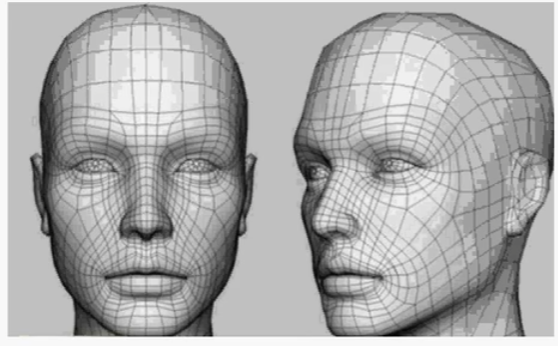
本章主要讨论三角网格。当然,任意多边形网格都能转换成三角网格。我们讨论的大多数概念对多边形和三角网格都适用。三角网格以其简单性而吸引人,相对于一般多边形网格,许多操作对三角网格更容易。当然,多边形在某些情况下具有优势,在差别很显著的时候我们会作出解释。
表示网格

对于某些应用程序,这种表示方法已经足够。然而,术语“网格”隐含的相邻三角形的联通性却在种简单表示中有任何体现。实际应用中出现的三角网格,每个二角形都和其他三角形共享边。于是三角网格需要存储三类信息:
- 顶点。每个三角形都有三个顶点。各顶点都有可能和其他三角形共享。
- 边。连接两个顶点的边。每个三角形有三条边。
- 面。每个三角形对应一个面。我们可以用顶点或边列表表示面。
根据应用程序的不同,有多种有效的网格表示方法,本章集中讨论一种标准存储格式:索引三角网格。
索引三角网格
在索引三角网格中,我们维护了两个列表:顶点表与三角形表。
每个顶点包含一个3D位置,也可能有如纹理映射坐标、表面法向量、光照值等附加数据。
通常,顶点列出的顺序是非常重要的,因为我们必须考虑“正面”和“反面”。从前面看时,我们将用顺时针方向列出项点。另外些信息也存在这一级中,如预先计算的表面法向量,表面属性(纹理映射)等。


注意到,索引三角形列表中的邻接信息是隐含的,例如:边信息没有直接存储,但我们还是可以通过搜索三角形表找出公共边。和前面“三角形数组”方式相比,这种方式确实能节省不少空间。原因是信息存于顶点级别,它的整数索引比之三角形数组里存储的顶点重复率要小得多。实践中,三角网里确实有大量的联通性问题。
高级技术
简单索引三角网格对于基本应用够了。但为吏加高效地实现某些操作还可以进行一些改进。主要的问题是邻接信息没有显式表达,所以必须从三角形列表中搜索。另一种表达方法可以在常数时间内取得这种信息。
方法是显式维护一个边列表,每边出两个端点定义,同吋维护一个共享该边的三角形列表。这样,三角形可视为三条边而非三个点的列表,也就是说它是边列表而不是点列表的索引。该思想的一个扩展称作“ winged edge”模型,对每一顶点,存储使用该点的边的索引。这样,三角形和边都可以通过定位点列表快迷査找,请见参考资料[8]和[9]。
针对渲染的特殊表达
大多数图形卡并不直接支持索引三角网。渲染三角形时,一般是将三个顶点同时提交。这样,共享顶点会多次提交,三角形用到一次就提交一次。因为内存和图形硬件间的数据传输是瓶颈,所以许多API硬件支持特殊的三角网格式以减少传输量。基本思想是排序点和面,使得显存中已有的三角形不需要再次传输。
从最高灵活性到最低灵活性,我们讨论三种方案:
- 顶点、索引缓存。它们存储在显卡的显存中,显存的速度极快,而普通的显示技术都是内存保存,速度稍慢。
- 三角带。
- 三角扇。
顶点缓存
说顶点缓存是一种特殊的存储格式,不如说是API和硬件之间的一种存储策略,用以发挥相续三角形顶点一致性的特点。通常,高级代码不需要了解顶点缓存是如何实现和执行的;后面我们会给出一些骤以最大限度地利用顶点缓存。
和其他缓存机制类似,顶点缓存基于最近使用的数据未来仍将被使用的原则。图形处理器缓存一小分(如,16个)最近使用的顶点,当AP要发送顶点时,首先探测级存内是否已存在。当然,这要求API了解图形卡缓存的大小和替换机制。若缓存内没有该顶点,则发生脱靶,API发送顶点,并更新缓存;若缓存内有该顶点,就命中,API通知图形卡“使用缓存内位置x的顶点“。
如前所述,顶点缓存其实是种底层的优化手段。任何三角网都可用高级代码实现止确渲染而不用考虑缓存。但进行顶点顺序的调整,使共享顶点的三角形集中发送有助于提高效率。这种调整只需要进行一次,并且可以离线进行。它只会对性能有帮助,不会使没有缓存的系统性能降低。参考附录B中的参考资料[14]以获得更多信息。
善用缓存,可能使发送到显卡的顶点数降低到平均每三角形少于一个。
三角带
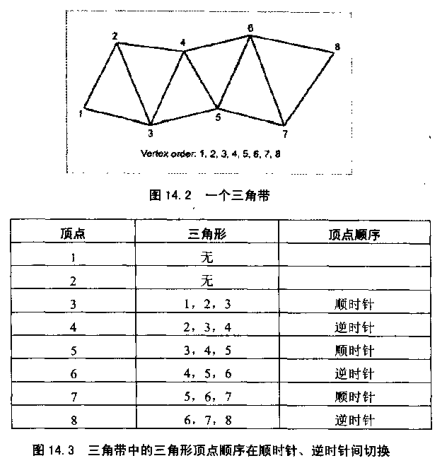
角带是一个三角形列表,其中每个三角形都与前一个三角形共享一边。图14.2显示了一个三角带的例子。注意顶点列出的顺序使得每三个连续的点都能构成一个三角形,例如:
- 点1,2,3构成第一个三角形。
- 顶点2,3,4构成第二个三角形。
- 顶点3,4,5构成第三个三角形。
在图14.2中,顶点以构成三角带的顺序编号。“索引”信息不再需要,因为项点顺序己经隐式定义了三角形。通常,列表前部有顶点数目,或末尾处有一特殊码表示“列表结束”。
注意到,顶点顺序在顺时针和逆时针间不断变换(见图14.3)。某些平台上,需要指出第一个三角形的顶点顺序,而有些平台上顺序是固定的。
- 点还是要多次发送给图形卡,从另一方面说,每个三角形至少要发送一个项点。但在顶点缓存机制下,有可能将每个三角形发送的顶点数降到一个以下。当然,顶点缓存需要额外的簿记信息(索引和缓存管理数据)。可是尽管这些额外信息对单个项点来讲相对较大,操作速度也会相对下降,但发送顶点数最少的系统在特定平台上速度最快。
- 我们希望最小化发往图形卡的顶点数,所以三角带的数目应尽可能少,即三角带越长越好。
- 另一个希望减少三角带数目的原因在于建立各三角带需要额外时间。从另一方面说,分别渲染两个长为n的三角带所需时间长于渲染一个长为2n的三角带,即使这个三角带中的三角形数多于两个分开带中角形数量的和。于是,我们经常通过使用退化三角形连接多个三角带,从而将整个网格置于一个连续的角带中。退化的意思是面积为零。图14.4显示了如何重复顶点以将两个三角带合并为一个。
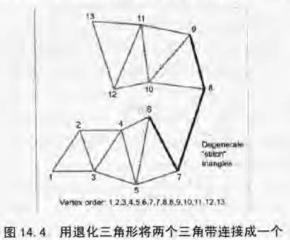
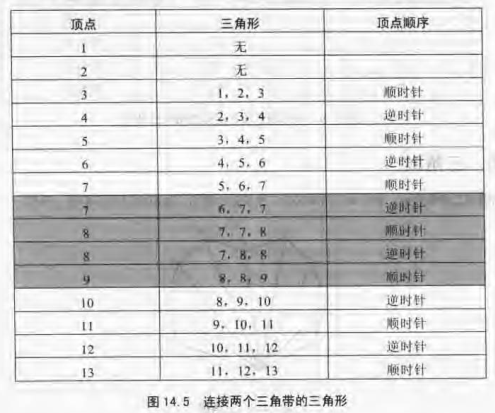
图14.4的含义不太明显,但这里有四个退化三角形用于连接两个三角带从而维持正确的顺时针,逆时针顺序。顶点7、8间的边实际包含两个退化三角形,图14.5指出了图14.4中包含的三角形。退化三角形面积为零不需渲染,所以不会影响效率,实际上要发送到图形卡的顶点仍然只是第一列的顶点:
1,2,3,4,5,6,7,7,8,8,9,10,11,12,13
这符合我们每三个连续顶点表示一个三角形的约定。
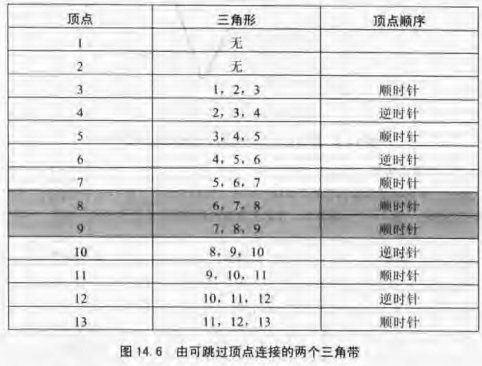
一些硬件(如PS2上的GS可以跳过三角带中的三角形,方法是通过一个顶点上的标志位指出“不必绘制”。此三角形这给我们一种方法可以有效的从任意点开始新三角带而不必重复顶点或使用退化三角形。例如,图14.4中的两个三角带可以如图14.6那样连接,其中灰色行表示顶点被标记“不必绘制”。
三角扇
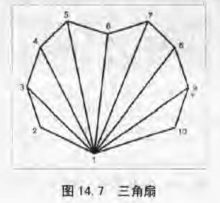
三角扇和三角带类似,但不如三角带灵活,所以很少使用。如图14.7所示即为三角扇:
三角网格类
法向量
- 在计算光照的时候需要法向量。
- 在3D模型背面进行剔除。
- 在模拟粒子在表面弹跳的效果。
- 加快正面检测碰撞。
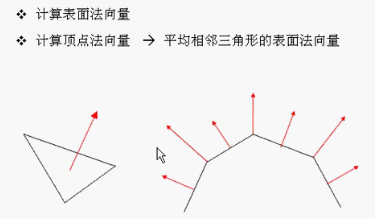
计算表面法向量

计算顶点法向量
一个顶点和很多三角形连接在一起的,计算方式是平均相邻三角形的表面法向量。
三角网格操作
逐片操作
三角网格是顶点和三角形的列表。逐片操作有两层含义:
- 一是对顶点的逐个进行操作,一个顶点一个顶点的操作。例如:要向三角网格应用转换,如旋转和缩放等。
- 二是逐三角形操作,一个三角形一个三角形的操作。例如:渲染三角网格。
焊接顶点
当两个或更多顶点相同(也许有误差)时,将它们焊接在一起是有益处的。更加准确地说,删除其余的,只剩一个。
焊接顶点的目的有两个。首先,去除重复顶点,节约内存。这是一种重要的优化方法,使得对网格的操作(如渲染和转换更快。其次,使几何上相邻的边在逻辑上也是相邻的。

需要注意在焊接之前需要去除孤立点,不然造成网格变形:
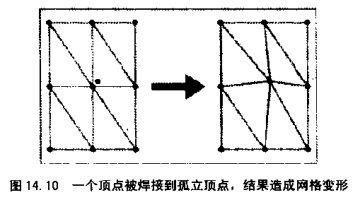
面拆分
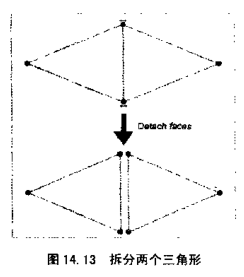
拆分即复制顶点,使边不再被共用。它和焊接刚好相反。显然,面拆分会导致拓扑间断,因为面不再邻接。而这正是我们的目的,使得几何间断的地方拓扑也足间断的(如角和边)。图14.13显示了两个角形的拆分。尽管我们把两个三角形分开以显示这里有多个边和顶点,这只是为了显示。顶点没有移动,新的顶点和边其实是重合的。
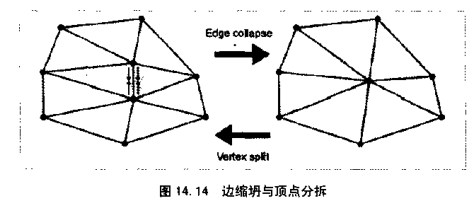
边缩坍和顶点拆分
边缩坍是将边缩减为项点的方法。与之对应的是顶点拆分。如图1414所小。注意到边缩坍使边的两个顶点变为一个,共享该边的三角形(图14.14中阴影部分)消失。边缩坍常用于网格消减(14.45节讨论)因为它减少了顶点和三角形数量。
网格消减
网格消减是将三角形和顶点数较多的网格变为三角形和顶点数相对较少的网格,并且要求网格外观和要顶点尽可能保持不变。
本文标签
游戏开发、3D数学基础:图形与游戏开发、Unreal Engine、游戏开发基础、数学、游戏开发数学基础、书籍笔记、笔记。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号