【3D数学基础：图形与游戏开发】笔记 第4~5章 向量

【3D数学基础：图形与游戏开发】笔记 第4~5章 向量

参考资料&原文链接

参考书籍：【3D数学基础：图形与游戏开发】 ISBN7-302-10946XTP.7262

(美) etcher Dun著、(美) an Arberry 清华大学出版社

GAMES101-现代计算机图形学入门-闫令琪

猎豹网校：游戏开发之3D数学基础

向量有关基础概念

向量

既有大小又有方向的量。

标量

只有大小没有方向的量。例如1，23，-1，0。

行向量

横着写的向量。例如：a = [2，10，7，4]。

列向量

竖着写的向量。例如：

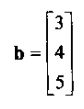
向量的维度

即向量有的成员的个数。例如 a = [1，4，13]，则a的维度是3。

向量的几何意义

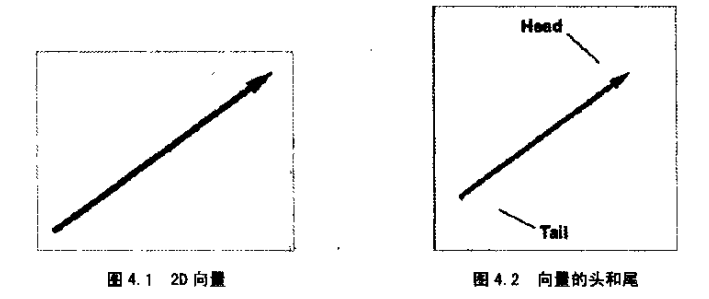
从几何意义上说，向量是有大小和方向的有向线段。注意：向量我们一般只关心它的大小和方向，不关心起点和终点的位置。例如：有两个向量指向的方向一致、大小相同，则我们认为它们是同一个向量，因为起点和终点之间的相对位置没有改变。它看起来就像一支箭，对吗？这是用图形描述向量的标准形式，因为向量定义的两个要素—大小和向都被包含在其中。有时候需要引用向量的头和尾，如图4.2所示，箭头是向量的末端(向量“结束”于，箭尾是向量的“开始”。

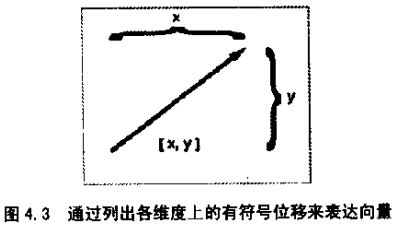
向量的表达

向量中的数表达了向量在每个维度上的有向位移。例如，图4.3中的2D向量列出的是沿x坐标方向和y坐标方向的位移：

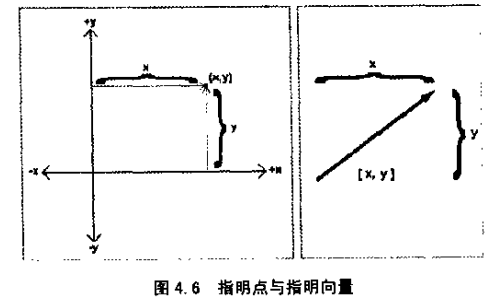
向量与点

“点”有位置，但没有实际的大小或厚度。上一节中学习了向量有大小和方向，但没有位置。所以使用“点”和“向量”的目的完余不同。“点”描述位置，而“向量”描述位移。图4.6比较了两幅图。一幅在第一章中用于展示点的位置，另一幅是本章前一节中展示向量的，它看上去显示出点和向量间有某种很强的联系。

零向量

任何集合，都存在加性单位元x，对集合中任意元素y，满足y+x=y。(这里使用的字体并不意味着只是标量集合，而是对任意集合。)

n维向量集合的加性单位元就是n维“零向量”它的每一维都是零。我们用黑粗体的零表示任意维零向量，如：

零向量的几何意义

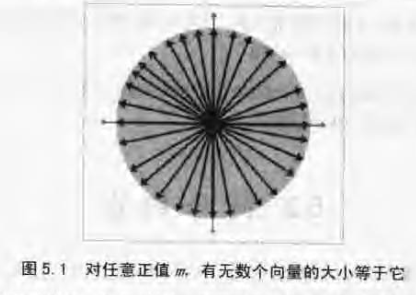
零向量非常特殊，因为它是值为零的向量。对于其他任意数m，存在无数多个大小(模)为m的向量。它们构成了一个圆。如图5.1所示。零向量也是唯一个没有方向的向量。虽然在图中表示零向量用的是一个点，但是认为零向量就是一个点并不准确，因为零向量没有定义某个位置。应该认为零向量表示的是“没有位移”，就像标量零表示的是“没有数量”一样。

负向量

对于任意集合，元素x的加性逆元为x，其与x相加等于加性单位元。简单的说就是x+(-x)=0，(再次提醒，尽管变量的字体表示标量，但我们讨论的是一般集合)从另一方面来说，集合中的元素能求负。负运算符也能应用到向量上。每个向量v都有一个加性逆元-v，它的维数和v的一样，满足v+(-v)=0。要得到任意维向量的负向量，只需要简单地将向量地每个分量都变负即可。数学表达式为：

将此法则运用到2D、3D、4D特例，有：

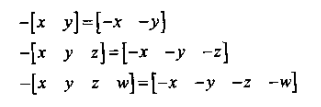
负向量的几何意义

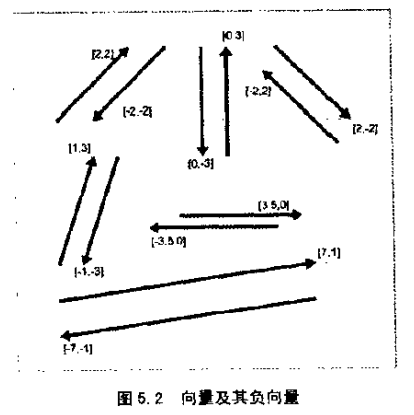
向量变负，将得到个和原向量大小相等，方向相反的向量。如图5.2所示：

向量的有关计算

数学中专门研究向量的分支称作线性代数。曾经提到过，向量在线性代数中只是一个数组。这个轴象念使我们制决许数学问愿如线性代数中，可以用单向和如解有n个未如的城性方程组。线性代数是一个非常有趣并且应用广泛的研究领域，但它与3D数学关注的领域并不相同。

向量大小（长度或模）

前面讨论过，向量有大小和方向。您可能已经注意到了，大小和方向都没有在向量中明确地表示出来。如2D向量{3，4}的大小既不是3，也不是4，而是因为向量的大小没有明确表示，所以需要计算。向量大小也常被称作向量的长度或模。

运算法则

几何意义

我们对公式5.4作更深入的研究。对2D中的任意向量v。能构造一个以v为斜边的直角三角形如图5.3所示。注意直角边的长度分别为分的绝对值。向量的分量可以为负，因为它们是有符号位移，但长度总是正的。由勾股定理可知，对于任意直角三角形，斜边长度的平方等于两直角边长度的平方和。应用到图5.3中就是：

向量与标量的乘除

虽然标量与向量不能相加，但它们能相乘。结果将得到一个向量，与原向量平行，但长度不同或方向相反。量与向量的乘法非常自接，将向量的每个分量都与标量相乘即可。标量与向量乘的顺序并不重要但经常把标量写在左边，数学表述为：

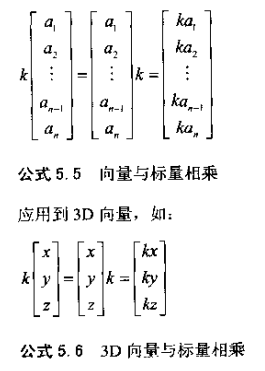
向量也能除以非零标量，效果等同于乘以标量的倒数：

示例：

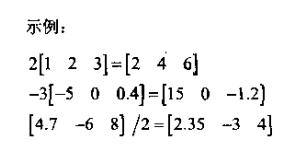
注意

• 标量与向量相乘时，不需要写乘号。将两个量挨着写即表示相乘(常将标量写在左边)。

• 标量与向量的乘法和除法优先级高于加法和减法。例如，3a+b是(3a)+b，而不是3(a+b)。

• 标量不能除以向量，并且向量不能除以另一个向量。

• 负向量能被认为是乘法的特殊情况，乘以标量-1。

几何意义

几何意义上，向量乘以标量k的效果是以因子k缩放向量的长度。例如，为了使向量的长度加倍，应使向量乘以2。如果k<0，则向量的方向被倒转。图5。4展示了向量被多个不同因子k乘的效果：

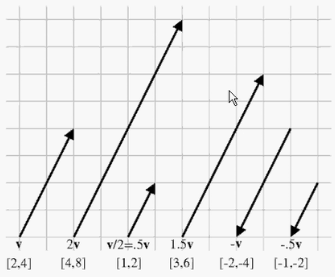
当k>=1时，向量长度按原方向长度加倍。

当0<k<1时，向量长度按原方向缩小。

当0=k时，向量变为0。

当0>k时，向量的方向将倒转，与乘以负向量相同。

标准化（归一化）向量：法线

对于许多向量，我们只关心它的方向而不关心其大小。如：“我面向的是什么方向？"，在这样的情况使用单位向量将非常方便。单位向量就是大小为1的向量，单位向量终常也被称作标准化向量或更简单地称为“法线”。

运算法则

几何解释

2D环境中，如果以原点为尾面一个单位向量，那么向量的头将接触到四心在原点的单位圆(单位圆的半径为1)，3D环境中，单位向量将触到单位球。图5.5中，用灰色箭头表示了若干2D向量，黑色箭头表示这些向量的标准化向量。

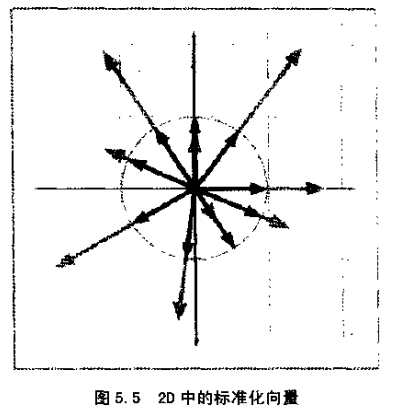
单位向量非常有用，在计算向量点乘的时候分母就为1了，这将大大简化我们的计算。特别是到了后面章节的几何图元和几何检测的时候，会及其频繁的使用单位向量。

向量的加法和减法

如果两个向量的维数相同，那么它们能相加，或相减。结果向量的维数与原向量相同。向量加减法的记法和标量加减法的记法相同。

运算法则

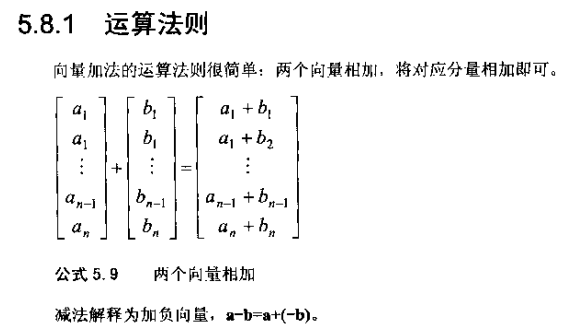
示例：

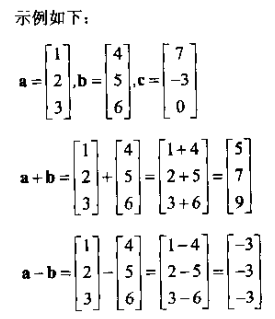
注意

• 向量不能与标量或维数不同的向量相加减。
• 和标量加法一样，向量加法满足交换律，但向量减法不满足交换律。永远有a+b=b+a，但a-b=(-a)，仅当a-b时，a-b=b-a。

几何意义

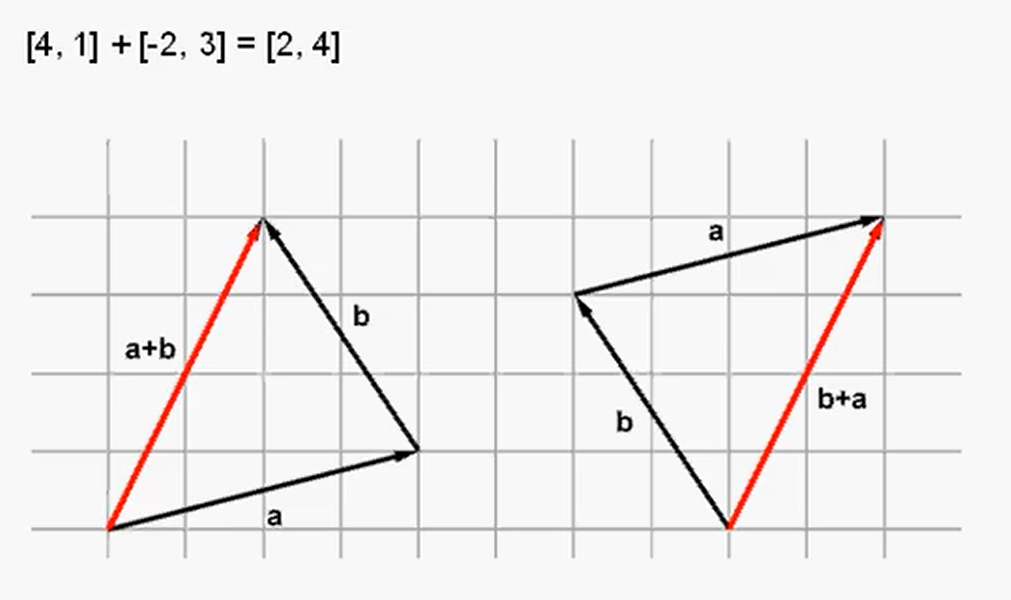
向量a和b相加的几何解释为：平移向量，使向量a的头连接向量b的尾，接着从a的尾向b的头画个向量。这就是向量加法的“三角形法则”。有的也使用“平行四边形法则”，是一样的。

向量的减法与之类似，如图所示。图证明了向量加法满足交换律，也证明减法不满足交换律。注意，向量a+b和向量b+a相等，但向量d-c和c-d的方向相反，因为d-c=-(c-d)。

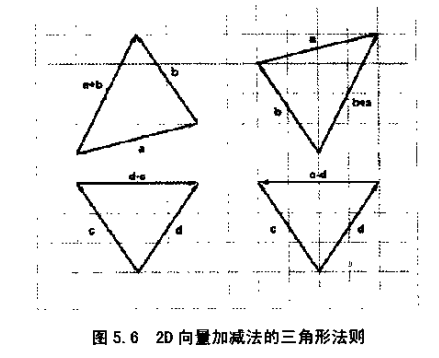
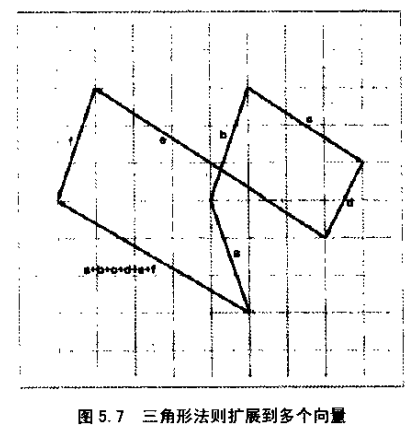
三角形法则能扩展到多个向量的情形中，如图所示：

一个点到另一个点的向量

计算一个点到另一个点的位移是种非常普遍的需求，可以使用三角形法则和向量减法来解决这个题。图展示了怎样用b-a计算a到b的位移向量：

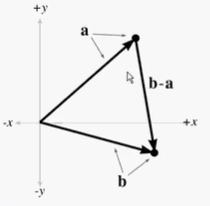
如上图所示，为了计算a到b的向量，将点和点b解释为从原点开始的向量，接着使用三角形法则事实上，在有些书中，向量确实被定义为两个点的减法。

注意，减法b-a代表了从a到b的向量。简单的求“两点之间”的向量是没有意义的，因为没有指明方向。求一个点到另一个点的向量才有实际意义。

向量的距离

首先，定义距离为两点间线段的长度。因为向量是有向线段，所以从儿何意义上说间的距离等于从一个点到另一个点的向量的长度。现在，让我们导出3D中的距离公式，先计算从在583节中我们已经学过如何进行这样的计算了。在3D情况中：

例子：

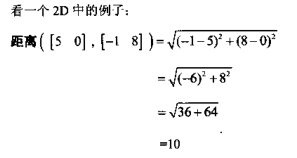
向量点乘（内积）

记法ab中的点号。与标量与向量的乘法一样，向量点乘的优先级高于加法和减法标量乘法和标量的乘法经常可以省略乘号，但在向量点乘中不能省略。点乘号量点乘就是对应分量乘积的和，其结果是个标量：

例子：

注意：点乘满足交换律：b · a = a · b。

几何意义

般来说，点乘结果描述了两个向量的“相似”程度，点乘结果越大，两向量越相近。几何解释更加直观：

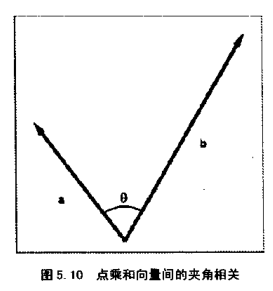
点乘结果解释

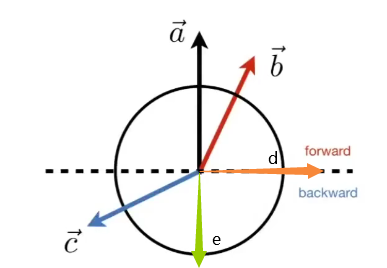
结果解释：

• cos0° = 1，结果->1（即>0）时，说明两向量较接近。例如a和b。
• cos90° = 0，结果->0（即=0）时，说明两向量垂直。例如a和d。
• cos180° = -1，结果->-1（即<0)时，说明两向量方向大致相反。例如a和e。

注意：

• 向量大小并不影响点乘结果的符号，所以上表是和a、b大小无关的。
• 如果a、b中任意一个为零，那么ab的结果也等于零。因此，点乘对零向量的解释是，零向量和任意其他向量都垂直。

向量投影

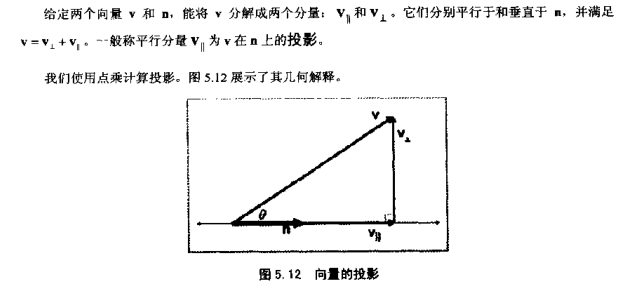
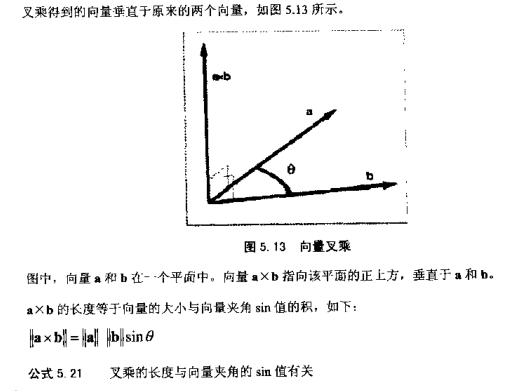
向量叉乘（叉积/法线/法向量）

和点乘一样，术语“又乘”来自记法a×b中的叉号。这里要把叉乘号写出来，不能像标量乘法那样省略它。叉乘公式为：

注意：

• 叉乘的运算优先级和点乘一样，乘法在加减法之前计算。当点乘和叉乘在一起时，叉乘优先计算a(bxc)，因为点乘返个标量，同时标量和向量间不能叉乘，所以(a·b)xc没有定义。运算a·(bxc)称作三重积。下节将给出此类运算的一些特殊性前面提到。
• 向量叉乘不满足交换律。事实上，它满足反交换律：axb=-(bxa)。
• 又乘也不满足结合律。般而言，(axb)×c≠ax(bxc)。有关叉乘的更多代数法则将在下节给出。

几何意义

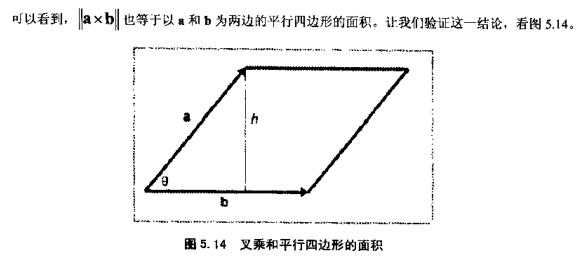
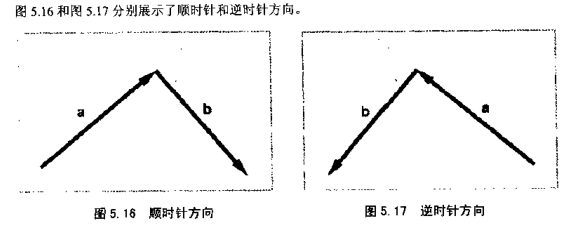
叉乘的方向

a×b垂直于a是垂直于a、b有两个方向。axb指向哪个方向呢？通过将a的头与b的尾相接，并检査从a到b是顺时针还是逆时针，能够确定a×b的方向。在左手坐标系中，如果和b呈顺时针，那么a×b指向您。如果a和b呈逆时针，a×b远离您。在右于坐标系中，恰好相反。如果和b呈顺时针，a×b远离您，如果a和b呈逆时针，a×b指向您。

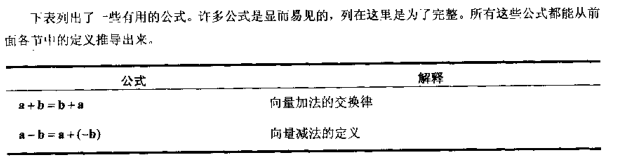
线性代数公式

本文标签

游戏开发、3D数学基础：图形与游戏开发、Unreal Engine、游戏开发基础、数学、游戏开发数学基础、书籍笔记、笔记。