1 2 3 4

Java 浮点数精确性探讨（IEEE754 / double / float）与 BigDecimal 解决方案

一、抛砖引玉

一个简单的示例：

double a = 0.0;
IntStream.range(0,3).foreach(i->a+=0.1);
System.out.println(a); // 0.30000000000000004
System.out.println(a == 0.3); //false

可以看到计算机因二进制&浮点数造成的问题离我们并不遥远，一个double经过简单的相加，便出现了影响正常性的结果。
我们可以通过 BigDecimal 来更详细展示：

BigDecimal _0_1 = new BigDecimal(0.1);
BigDecimal x = _0_1;
for(int i = 1; i <= 10; i ++) {
	System.out.println( x + ", as double "+x.doubleValue());
	x = x.add(_0_1);
}

输出：

0.1000000000000000055511151231257827021181583404541015625, as double 0.1
0.2000000000000000111022302462515654042363166809082031250, as double 0.2
0.3000000000000000166533453693773481063544750213623046875, as double 0.30000000000000004
0.4000000000000000222044604925031308084726333618164062500, as double 0.4
0.5000000000000000277555756156289135105907917022705078125, as double 0.5
0.6000000000000000333066907387546962127089500427246093750, as double 0.6000000000000001
0.7000000000000000388578058618804789148271083831787109375, as double 0.7000000000000001
0.8000000000000000444089209850062616169452667236328125000, as double 0.8
0.9000000000000000499600361081320443190634250640869140625, as double 0.9
1.0000000000000000555111512312578270211815834045410156250, as double 1.0

二、不精确的原因

常听说double&float不精确，ieee754标准什么的，难道是标准导致的问题吗？
原因：问题是多综合因素导致的，而当下 iEEE754 标准则是各方面权衡下的尽可能逼近正确结果的一种方案

1. 二进制的必然局限

正如10进制下 1/3 = 0.333…无法精确表示，在二进制中若想表示1/10，则也是无限循环小数
具体的 \(0.1_{(10)}=0.0010011001100110011..._{(2)}\)
这就本质上造成了若不以分数表示，一些其他进制中的精确数值在二进制中无法以有限位精确表示

2. 计算机中数值存储方案

计算机中CPU对数值的存储&运算没有分数表示，而是以有有限位bit进行。（当然，可能会疑问为什么不以一定规则用分数精确存储，并附上相应的一套运算规则？可参考这个讨论）

因此对于无限小数，存储位数一定的情况下必然会造成数值丢失。
如：\(0.1_{(10)}*3\) 在二进制 8bit 规则（若是单纯截断，没有舍入）下，结果为 \(0.00011001_{(2)}* 3=0.01001011_{(2)}=0.29296875_{(10)}\) 而不会是 0.3
这就如 \(0.1_{(3)}*3\) 在十进制计算机中（若是单纯截断）结果是 0.99999999 而不会是 1

3. 计算机数值表示规范 IEEE-754

根据上述讨论，便能认知到对于数值的存储和计算规则是可以千变万化的。
因此 IEEE 协会为了规范统一（方便CPU指令制造，各平台兼容等等）出台了 IEEE Standard for Floating-Point Arithmetic（IEEE-754）二进制浮点数算数标准，选用了浮点数作为储存和算数标准。
该标准描述了包括"浮点数的格式"、"一些特殊数值"、"浮点数的运算"、"舍入规则与例外情况" 等等内容

三、IEEE-754 标准"部分"概述

1. 它定义了5种基本格式：

binary32、binary64、binary128、decimal64、decimal128
其中 binary32、binary64 便是常说的 float、double

2. float、double解析：

以 binary64（double）为例：
它具有以下格式：

  • sign：符号位，0为正，1为负
  • exponent：无符号整数，此处范围为[0,2047]。实际应用时会加上一固定的偏移量，该偏移量根据exponent长度有所不同，而此处double 为 -1023，因此实际应用范围为[-1022,1023]（缺少-1023和+1024是因为全0全1为特殊保留字）
  • precision：精度值，存储有效数字（隐式的整数位1并不包含其中）
    image

其最终值结果表达式为： \((-1)^{sign}*1.fraction_{(2)}*2^{e-1023}\)
基于这种格式，这也是为什么数越大精度越低，越小精度越高。因为越大则fraction中整数占位越多，而小数占位则越少。（下图可见，小数部分已全部舍去，整数部分都开始舍入）
image

binary 32（float）同理：偏移量为 -127
image

3. 舍入规则：

IEEE-754 仅提供了一些舍入规则，但没有强制说选用某种规则，具体规则的选用由具体实现决定。
以下是一些规则：

  • Roundings to nearest 就近舍入
    • Round to nearest, ties to even：就近舍入。若数字位于中间，则偏向舍入到偶数最低有效位
    • Round to nearest, ties away from zero：就近舍入。偏向远离0，即四舍五入。
  • Directed roundings 定向舍入
    • Round toward 0：朝向0舍入
    • Round toward +∞：朝向+∞舍入
    • Round toward −∞：朝向-∞舍入

而在 Java 中，默认舍入模式为 RoundingMode.HALF_EVEN，即 "Round to nearest, ties to even"
该舍入模式也被称为 "Banker's rounding"，在统计学上这种模式可以使累计的误差最小

4.手动计算IEEE754值示例

以常见的 0.1 和 float 为例：
\(0.1_{(10)}=0.0001100110011..._{(2)}=(-1)^0*1.100110011...01_{(2)}*2^{(123-127)}\)

因此 IEEE-754，存储的实际值为 0.10000000149011611938
image
可见，有效数字其实已经尽最大可能的去保留精度，无奈位数有限，并在最后做了舍入。

5.其他解决方案探讨

IEEE-754 浮点数不过是一种标准，它是性能&存储空间&表示范围&精度各方面权衡下的一个结果。正如上述和stackexchange所讨论的，若对精度或其他方面有着更高的需求，则可以另一套规则定义数值的存储和计算。

Decimal 便是其中的一种。摘一段网上的介绍

Decimal types work much like floats or fixed-point numbers, but they assume a decimal system, that is, their exponent (implicit or explicit) encodes power-of-10, not power-of-2. A decimal number could, for example, encode a mantissa of 23456 and an exponent of -2, and this would expand to 234.56. Decimals, because the arithmetic isn't hard-wired into the CPU, are slower than floats, but they are ideal for anything that involves decimal numbers and needs those numbers to be exact, with rounding occurring in well-defined spots - financial calculations, scoreboards, etc. Some programming languages have decimal types built into them (e.g. C#), others require libraries to implement them. Note that while decimals can accurately represent non-repeating decimal fractions, their precision isn't any better than that of floating-point numbers; choosing decimals merely means you get exact representations of numbers that can be represented exactly in a decimal system (just like floats can exactly represent binary fractions).

Decimal（十进制）的工作方式与 fixed-point（定点数）非常相似，只是以十进制为基础（指乘数为10的幂，而非2的幂），例如 234.56=23456*10^(−2) 可以扩展为 23456 与 -2，因为都是整数所以精确存储。
但 Decimal 并不会就比浮点数精确度高，正如其名十进制，它仅可以精确表示能在十进制中精确表示的数。而十进制中本身就无法精确表示的数，如 \(0.1_{(3)}\)，其依然无法精确保存。

四、Java 中 BigDecimal 实现概述

不可变的，任意精度的有符号十进制数。

因十进制小数对二进制的转化是不精确的，因此它将 \(原值*10^{(scale)}\) 扩展为整数后，后通过 long intCompat 来存储扩展后部分。
并在需要真实值时，再计算还原 \(intCompact * 10^{(-scale)}\)
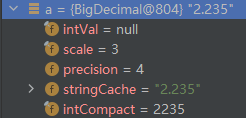
image

BigDecimal 常见API&情形：

  1. setScale(int newScale, RoundingMode roundingMode)
    设置该BigDecimal的小数点后精度位数，若涉及到数值舍入，必须指定舍入规则，否则报错。
    如：保留2位小数，截断式：.setScale(2, RoundingMode.DOWN)

五、延申

1. 定点数(fixed-point)解决方案

定点数在实现上并不是字面意思固定某位为小数点分别存整数和小数
同Decimal实现一样，先将原值扩展到到足够大的整数，并存下scale，以后续还原真实值

2. 各语言情况及解决概览

https://0.30000000000000004.com

3. 为什么数据库MYSQL SELECT (0.2+0.1)=0.3 返回 true？

参考：https://stackoverflow.com/a/55309851/9908241
答：在显式精确数值计算时，Mysql 可能会使用 Precision Math 计算（ https://dev.mysql.com/doc/refman/8.0/en/precision-math-examples.html ）
即 SELECT (0.1+0.2) = 0.3 或多或少可能以如下方式执行实际查询:SELECT CAST((0.1 + 0.2) AS DECIMAL(1, 1)) = CAST((0.3) AS DECIMAL(1, 1));

IEEE 754 标准浮点数的精度问题是仍然存在的，以下通过显式声明浮点类型可复现：

create table test (f float);
insert into test values (0.1), (0.2);
select sum(f) from test; // 输出经典 0.30000000447034836

4. 浮点数为什么会这样设计，为什么exponent需要偏移量

可参考：IEEE 754格式是什么? - wuxinliulei的回答 - 知乎

撰文参考：
- 0.1d相加多次异常展示： https://stackoverflow.com/questions/26120311/why-does-adding-0-1-multiple-times-remain-lossless
- 数值存储&计算多种解决方案讨论： https://softwareengineering.stackexchange.com/questions/167147/why-dont-computers-store-decimal-numbers-as-a-second-whole-number/167151#167151
- 十转二进制计算教学 How to Convert a Number from Decimal to IEEE 754 Floating Point： https://www.wikihow.com/Convert-a-Number-from-Decimal-to-IEEE-754-Floating-Point-Representation
- 计算IEEE-754全步骤（可自定数字） https://binary-system.base-conversion.ro/convert-real-numbers-from-decimal-system-to-32bit-single-precision-IEEE754-binary-floating-point.php
- CSDN https://blog.csdn.net/weixin_44588495/article/details/97615664
- https://en.wikipedia.org/wiki/IEEE_754
- https://en.wikipedia.org/wiki/Double-precision_floating-point_format
- https://en.wikipedia.org/wiki/Single-precision_floating-point_format
- http://cr.openjdk.java.net/~darcy/Ieee754TerminologyUpdate/2020-04-21/specs/float-terminology-jls.html
- IEEE754 在线转换网站： https://www.binaryconvert.com/result_float.html
- 十进制-二进制（可小数）在线转换： https://www.mathsisfun.com/binary-decimal-hexadecimal-converter.html
- https://0.30000000000000004.com

posted @ 2021-08-10 16:33  SimpleIto  阅读(1609)  评论(0)  编辑  收藏  举报