正则表达式不要背

本文从文件依赖依赖这个需求切入, 详细阐述了文件依赖分析的实现过程, 对于其中所使用到的正则表达式进行原理上的分析, 说明了状态机的基本架构以及状态机的最小实现。

从文件依赖分析需求说起

如果我想获取某个文件的所有依赖（如下图中的紫色部分）, 应该怎么做呢

【方案1】利用 webpack 打包后通过 babel 编译拿到 ast 中对应的引入部分
【方案2】直接使用正则进行提取

两种方案各有优劣, 由于本文的内容是跟正则相关的, 【方案1】最后拿到的 ast 也是通过正则匹配得到的, 所以直接一步到位, 阐述一下【方案2】的实现过程以及其中的原理

假设只提取 require 关键字引入的模块

提取的代码以及流程图如下所示

const reg = /require\((")([^\1]+?)\)/gm

但是上述代码只能提取单个关键词引入的模块, 但是 JS、CSS、HTML 都有这不同的模块引入关键词, 而 JS 因为历史原因有着不止一种模块引入关键词, 要完整地提取文件中的引入模块, 就得一个个地分析这些引入关键词的词法规则, 再根据词法规则去写对应的正则表达式进行提取

提取所有模块

const reg = /(src|require|import|url|from).(['"`~(])([^(\2)]+?)(\)|\2)/gm

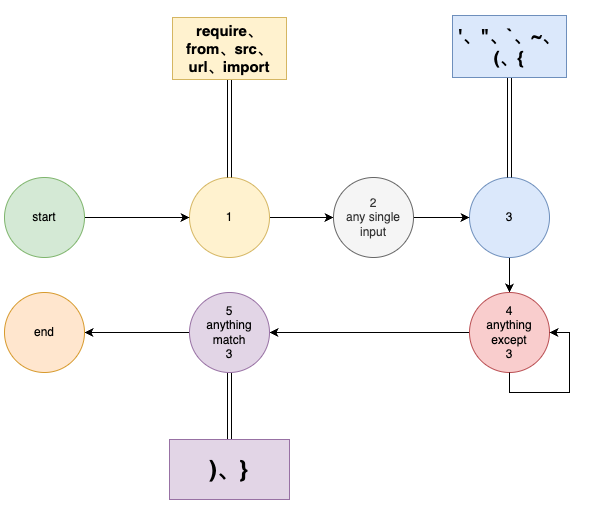
上图是提取所有模块引入关键字 引入模块的一个状态转移图, 每个状态接受不同的输入, 然后进入下一个状态，这就是一个简单的状态机, 在引入状态机之前, 先简单说明一下正则表达式的定义

正则表达式原理

正则表达式的定义

对于给定的字符集：Σ = {c1, c2, ..., cn}，有
1. ε（空字符串）是正则表达式
2. 对于任意 c ∈ Σ，c 是正则表达式
3. 如果 M、N 是正则表达式，那么以下都是正则表达式
   - 选择：M | N == {M, N}
   - 连接：MN == {mn | m ∈ M, n ∈ N}
   - 闭包：M* == {ε, M, MM, MMM, ...}

以上为正则表达式的基本构造，都是一些离散数学的术语，看起来难免有些抽象。所以为了简化正则表达式，就有了正则表达式的语法糖：

1. [c1-cn] == c1|c2|...|cn
2. c+ == 一个或者多个 c
3. c? == 一个或者零个 c
4. "c*" == 就是 c* 本身，不是闭包，类似转义
5. c{i, j} == i 个到 j 个 c 的连接
6. 点 (.) == 除了 '\n' 之外的任意字符

如何去测试一个字符串是否通过了正则表达式的规则呢？

这就引出了状态机的定义

状态机的架构

输入的字符串 => 状态机 => yes/no

即，状态机会告诉你，它能不能接受或者说识别你输入的字符串，可以回答 yes，否则回答 no。更加规范的描述是：

M = (Σ, S, q0, F, δ)

- Σ: 字母表
- S: 状态集
- q0: 初始状态 
- F: 终结状态集
- δ: 转移函数

举个例子：

对于这个图来说：

- Σ: {a, b}
- S: {0, 1, 2}
- q0: {0}
- F: {2}
- δ: {
  (q0, a) -> q1,
  (q0, b) -> q0,
  (q1, a) -> q2,
  (q1, b) -> q1,
  (q2, a) -> q2,
  (q2, b) -> q2,
}

接受的定义是，输入串消耗完毕之后，最后的状态一定要是终结状态，假如输入的字符串 S = abab，那显然是可以被接受的。

我们再详细地看它的转移函数，每个状态，遇到特定的一个输入，都只有一个路线可以走，那么这种状态机就叫做 DFA(确定状态有限状态自动机) 。

NFA 与 DFA

DFA (确定状态有限状态自动机)

所以有限状态机的工作过程，就是从开始状态，根据不同的输入，自动进行状态转换的过程。

开始状态：圆圈表示状态，被一个“没有起点的箭头”指向的状态，是开始状态，上例中是 S1
最终状态：也叫接受状态，图中用双圆圈表示，这个例子中也是 S1
输入：在一个状态下，向状态机输入的符号/信号，不同输入导致状态机产生不同的状态改变
转换：在一个状态下，根据特定输入，改变到特定状态的过程，就是转换

上图中的状态机的功能，是 检测二进制数是否含有偶数个 0 。从图上可以看出，输入只有 1 和 0 两种。从 S1 状态开始，只有输入 0 才会转换到 S2 状态，同样 S2 状态下只有输入 0 才会转换到 S1。所以，二进制数输入完毕，如果满足最终状态，也就是最后停在 S1 状态，那么输入的二进制数就含有偶数个 0。

NFA (非确定状态有限状态自动机)

DFA 最大的特点就是「在一个状态下，输入一个符号，一定是转换到确定的状态，没有其他的可能性。」而 NFA，就不止一个可能性。

举个例子，对于正则表达式 ab|ac，对应 NFA 可以是这样的：

可以看到，在状态 1 这里，如果输入 a，其实有两种可能，如果后面的符号是 b，那么可以匹配成功，后面符号是 c 也能匹配成功。所以状态机在执行过程中，可能要尝试所有的可能性。在尝试一种可能路径匹配失败后，还要回到之前的状态再尝试其他的路径，这就是 「回溯」 。

但是 DFA 消除了这种不确定性，所以可以想见，其执行性能应该要比 NFA 更好，因为不需要回溯。
但是，因为 DFA 引擎只包含有限的状态，所以它不能匹配具有反向引用的模式；并且因为它不构造显示扩展，所以它不可以捕获子表达式。

DFA 与 NFA 的本质区别

DFA: 对于任意字符, 最多有一个状态可以转移 —— 以文本为主导

NFA: 对于任意字符, 有多于一个状态可以转移 —— 以表达式为主导

更多关于 NFA 与 DFA 的区别

如何将正则表达式转换成 NFA (Thompson算法)

正则表达式的定义

ε，即空字符串
c，即单个字符
e1e2，连接
e1|e2，选择
e1*，闭包

Thompson 算法中使用最基本的两种转换：

正则表达式中的各种运算，可以通过组合上述两种转换实现：

组合运算 RS：

选择运算 R|S：

闭包运算 R* ：

这样我们把正则表达式视为一系列输入和运算，进行分解、组合，就可以得到最终的 NFA。

为什么会有空字符串路径存在

在 Thompson 算法中，空字符串的路径存在的原因是为了处理正则表达式中的基础语法规则，例如 a|b、ab、a* 等。这些语法规则中可能存在空字符串，例如 a| 表示匹配字符串中的 a 或空字符串。为了实现这些语法规则，我们需要在 NFA 中引入空字符串的路径，以便在状态转换时能够处理空字符串的情况。

具体来说，我们可以将空字符串看作是一种特殊的输入符号，例如用 ε 表示空字符串。在 Thompson 算法中，我们可以在状态之间引入 ε 转换，表示可以在两个状态之间跳转而无需输入任何字符。这种转换路径可以用来处理空字符串的情况。例如，对于正则表达式 a|b，我们可以将其转换为两个状态之间存在一个 ε 转换的 NFA，表示可以匹配字符串中的 a 或 b 或空字符串。

DFA的简单实现(dom的词法分析)

有这样一个dom, <p>content</p>，它的状态机如下所示。

状态机的实现如下所示

const str = `<p>text</p>`

const State = {
  initial: 1, // 初始状态
  tagOpen: 2, // 标签开始状态
  tagName: 3, // 标签名称状态
  text: 4, // 文本状态
  tagEnd: 5, // 标签结束状态
  tagEndName: 6 // 结束标签名称状态
}

function isAlpha(char) {
  return char >= 'a' && char <= 'z' || char >= 'A' && char <= 'Z'
}

function DFAForDom(str) {
  let currentState = State.initial
  const chars = []
  const tokens = []
  while(str) {
    const char = str[0]
    switch (currentState) {
      case State.initial:
        if (char === '<') {
          currentState = State.tagOpen
          str = str.slice(1)
        } else if (isAlpha(char)) {
          currentState = State.text
          chars.push(char)
          str = str.slice(1)
        }
        break
      case State.tagOpen:
        if (isAlpha(char)) {
          currentState = State.tagName
          chars.push(char)
          str = str.slice(1)
        } else if (char === '/') {
          currentState = State.tagEnd
          str = str.slice(1)
        }
        break
      case State.tagName:
        if (isAlpha(char)) {
          chars.push(char)
          str = str.slice(1)
        } else if (char === '>') {
          currentState = State.initial
          tokens.push({
            type: 'tag',
            name: chars.join('')
          })
          chars.length = 0
          str = str.slice(1)
        }
        break
      case State.text:
        if (isAlpha(char)) {
          chars.push(char)
          str = str.slice(1)
        } else if (char === '<') {
          currentState = State.tagOpen
          tokens.push({
            type: 'text',
            content: chars.join('')
          })
          chars.length = 0
          str = str.slice(1)
        }
        break
      case State.tagEnd:
        if (isAlpha(char)) {
          currentState = State.tagEndName
          chars.push(char)
          str = str.slice(1)
        }
        break
      case State.tagEndName:
        if (isAlpha(char)) {
          chars.push(char)
          str = str.slice(1)
        } else if (char === '>') {
          currentState = State.initial
          tokens.push({
            type: 'tagEnd',
            name: chars.join('')
          })
          chars.length = 0
          str = str.slice(1)
        }
        break
    }
  }

  return tokens
}

console.log(DFAForDom(str))