算法笔记（六）：计数排序和基数排序
（一）说明
这里我是按自己的理解去实现的，时间复杂度和空间复杂度和算法导论上的可能不一样，感兴趣的话参考下就行，感觉最重要的还是算法思想。根据算法性能去实现算法以后再研究。
（二）计数排序
计数排序的基本思想是：对每一个输人元素x，确定小于x 的元素个数。 利用这一信息，就 可以直接把x放到它在输出数组中的位置上了。 例如，如果有17个元素小于x，则x就应该在第18个输出位置上。 当有几个元素相同时，这一方案要略做修改。 因为不能把它们放在同一个输出位置上。
从这段话我们可以得出，我们要处理的事情其实就2个：
1、获取小于x的元素的个数k，然后将x放到k+1的位置上（当然，因为python列表的索引是从0开始的，所以代码就没必要+1了，直接放到索引k上就行了（就比如：有4个元素小于X，那么此时A[4] = X就行了，因为A[0] A[1] A[2] A[3]））
2、处理相同元素的情况。
实现代码：
1 #计数排序 2 def conutingSort(A): 3 B = [0 for i in range(len(A))] #初始化输出序列 4 #2个for循环获取小于X的元素的个数，5-9行 5 for i in range(len(A)): 6 k = 0 7 for j in range(len(A)): 8 if A[i] > A[j]: 9 k += 1 10 #这个IF else，处理同名元素的情况，B.count(A[i])返回A[i]元素出现的个数 11 if A[i] in B: 12 B[k + B.count(A[i])] = A[i] 13 else: 14 B[k] = A[i] 15 return B 16 17 A = [5,2,4,7,1,3,2,6,-1,-6] 18 19 print(conutingSort(A))
（三）基数排序
感觉这种方式单独对正整数进行排序还好，如果考虑负数和小数的问题，问题有点复杂，甚至于可能要借用其他排序算法去处理。看算法导论上面的意思好像也是针对正整数的排序算法，感觉写这本书的大牛文笔好像不太好，没有深入浅出的感觉，或者是翻译的文笔不行。
基数排序，我个人的理解是，例如：对列表A = [720,328,278,356,789,234,123]进行排序
1、先按个位数进行排序 ，得到结果[720,123,234,356,328,278,789]
2、在第一步的基础上，按十位数进行排序，得到结果[720,123,234,328,356,278,789]
3、在第二步的基础上，按百位数进行排序，得到结果[123,234,278,328,356,720,789]
这样，有多少位数，就执行多少轮。最重要的是：每一轮结束时，一定要更新列表，然后下一轮排序是在这个的基础上进行的
实现代码：
**就是幂，例如x**y 就是 x的y次幂
% 返回除法的余数
[a for b in s for a in b] 这个是2重的列表生成式，不了解列表生成式的可以单独去了解下
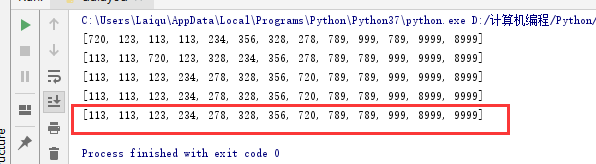
1 #基数排序 2 def radixSort(A, d): # 最大位数是几，d就填几 3 for i in range(d): # d轮排序 4 s = [[] for k in range(10)] 5 for j in A: 6 s[int(j / (10 ** i)) % 10].append(j) 7 A = [a for b in s for a in b] #更新列表A 8 print(A) 9 return A 10 11 A = [720,328,278,356,789,234,123,113,113,999,789,9999,8999] 12 13 print(radixSort(A,4))
可以看到，前面4个就是每一轮排序后的结果
