算法笔记（四）：堆排序
#说的还是感觉不够清晰，感兴趣的勉强看看吧
（一） 堆
这里的堆指的是堆数据结构，不是Java中的垃圾收集器。堆可以理解为一个近似的完全二叉树，如下图，除了最底层之外该树是完全满的，并且是从左往右填充。（最底层只是不要求填充满，不是不能填充满）
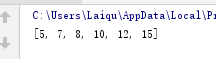
例如：[5, 7, 8, 10, 12, 15]（小顶堆）
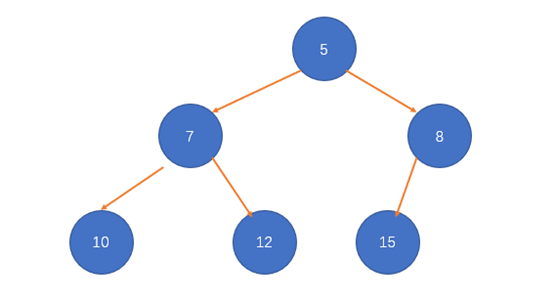
（二） 堆的性质
软件设计师考试资料中对于堆的定义，要满足下面的公式。
（三） 堆排序的过程
分为2个过程：
1、 建立大顶堆或小顶堆。（简单的说，就是把列表排成符合上面列出来的公式）
2、 对大顶堆或小顶堆进行排序
（四） 建立大顶堆（理解了大顶堆，小顶堆差不多，可以自己尝试实现，可能写一遍就比较清晰了）
从第二点中我们知道，要建立大顶堆，就要维护下面的性质。
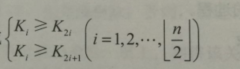
例如：[15, 12, 10, 8, 7, 5] 就满足上面的性质。（这里我们就当列表的索引从1开始，而不是从0开始）
实现代码：
1 #建堆 2 def buildHeap(A): 3 #这里在首位插入一个X是为了方便比较（因为python列表的索引从0开始），目的是为了方便维护堆的性质（Ki >= K2i 和Ki >= K2i+1） 4 #例如：传入的列表是[12,5,7,8,10,15]，这里就变成 ['X',12,5,7,8,10,15] 5 #所以我们要处理数据实际上是A[1],A[2]...A[n] 6 #这个'X'永远用不上，唯一的作用就是让我们要处理的数据从A[1]开始 7 A.insert(0,'X') 8 #获取列表中间元素的索引，因为python列表的索引从0开始（但是获取长度的时候却不是这样），所以这里减1后获取我们需要处理的列表的长度A[1]...A[n] 9 k = (len(A)-1)//2 10 #这边range(k,0,-1) 意思是 i = k ,i = k-1 ...（最小为1，不会等于0） 11 for i in range(k,0,-1): 12 maxHeap(A,i) 13 return A 14 #维护大顶堆的性质 15 def maxHeap(A,i): 16 #为了维护 Ki >= K2i 和Ki >= K2i+1,先获取相应的索引（下标） 17 largest = i 18 k1 = 2*i 19 k2 = 2*i+1 20 #第一个条件：这里加这个条件是因为，递归调用maxHeap的时候，2i有可能大于列表长度， 21 # 在调试模式下看这个函数的执行过程就清楚了。 22 #第二个条件：比较大小（对应到公式就是，如果Ki < K2i） 23 if k1 < len(A) and A[i] < A[k1]: 24 largest = k1 25 if k2 < len(A) and A[largest] < A[k2]: 26 largest = k2 27 #条件成立就交换数据，不成立说明A[i]已经是最大了，函数结束 28 if largest != i: 29 #交换A[i] A[largest]的值 30 A[i],A[largest] = A[largest],A[i] 31 #交换数据后，以该节点为根的子树可能违反大顶堆的性质，所以递归调用自身 32 maxHeap(A,largest)
（五） 对大顶堆进行排序
排序的过程就是在大顶堆的基础上,重复1、2、3步骤（这里请注意，我们的列表的第一个元素是‘X’，需要处理的数据是从A[1]开始的）
1、交换A[1] A[len(A)-1]。（就是将列表第一个数据和最后一个数据交换，因为交换前是大顶堆，交换后，列表最后一个数据就是最大的了）
2、删除列表末尾的数据，添加到结果列表中。
3、数据交换后，大顶堆的性质肯定不成立了。所以调用maxHeap（）维护大顶堆的性质
1 #堆排序 2 def heapSort(A): 3 # 这里返回的是一个大顶堆 4 A = buildHeap(A) 5 #python列表的索引从0开始，所以-1后才是最后一个元素的索引 6 k = len(A)-1 7 result = [] 8 while k >0: 9 #将A[1]和A[k]交换 10 A[1],A[k]= A[k],A[1] 11 #删除A列表末尾的数据，添加到result列表中 12 result.insert(0,A.pop()) 13 # result.append(A.pop()) 14 k -= 1 15 maxHeap(A,1) 16 return result
（六） 完整代码
1 #建堆 2 def buildHeap(A): 3 #首位插入一个元素，方便比较 4 A.insert(0,'X') 5 k = (len(A)-1)//2 6 for i in range(k,0,-1): 7 maxHeap(A,i) 8 return A 9 #维护大顶堆的性质 10 def maxHeap(A,i): 11 largest = i 12 k1 = 2*i 13 k2 = 2*i+1 14 if k1 < len(A) and A[i] < A[k1]: 15 largest = k1 16 if k2 < len(A) and A[largest] < A[k2]: 17 largest = k2 18 if largest != i: 19 A[i],A[largest] = A[largest],A[i] 20 #交换数据后，以该节点为根的子树可能违反大顶堆的性质，所以递归调用自身 21 maxHeap(A,largest) 22 #堆排序 23 def heapSort(A): 24 A = buildHeap(A) 25 k = len(A)-1 26 result = [] 27 while k >0: 28 A[1],A[k]= A[k],A[1] 29 result.insert(0,A.pop()) 30 # result.append(A.pop()) 31 k -= 1 32 maxHeap(A,1) 33 return result 34 35 B = [12,5,7,8,10,15] 36 37 print(heapSort(B))
