算法笔记（二）：贪心算法

（一）    贪心法

贪心法在解决问题的策略上是根据当前已有的信息做出选择，不管将来有什么结果，这个选择都不会改变。换言之，贪心法并不是从整体最优考虑，它所做出的选择只是某种意义上的局部最优。

用贪心法求解的问题一般具有2个重要的性质：

（1）   最优子结构：当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构。问题的最优子结构是该问题能采用贪心法求解的关键性质。

（2）   贪心选择性质：指问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来得到。这也是贪心法和动态规划法的主要区别。

（二）    示例1

设有0,1,…,n-1个物品，体积分别为v₀,v₁,…,v_n-1 ，将这些物品装入容量都为v的若干个箱子中，不同的装箱方案所需要的箱子数目可能不同，装箱问题要求使装尽这n种物品的箱子数最少。

约定：

（1）   物品体积不超过箱子容量。

（2）   现有的箱子足以装入所有物品

（3）   物品不能拆分

算法描述：

输入物品列表信息

输入箱子列表信息

将物品列表按体积降序排序（从大到小）

    while 还有物品未装入箱子：

        if 物品体积 <= 箱子容量：

             将物品装入箱子

             更新箱子容量

             物品列表中移除已经装入箱子的物品

         else：（如果当前箱子不足以装入物品）

              获取下一个箱子的索引

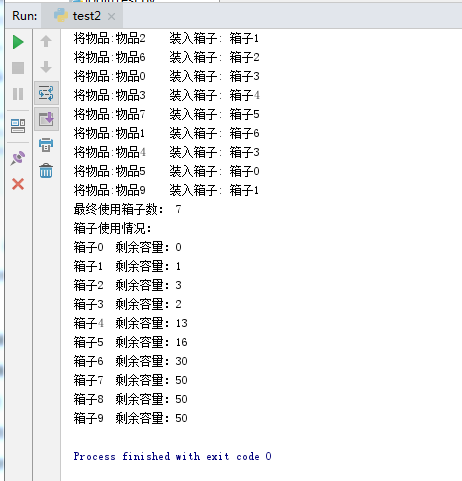
import random
import operator
#物品类
class goods():
    def __init__(self,goods_name,goods_v):
        self.goods_name = goods_name #物品名称
        self.goods_v = goods_v   #物品体积
#箱子类
class box():
    def __init__(self,box_name):
        self.box_name = box_name #箱子名称
        self.box_v = 50  #箱子容量

#贪心算法实现，goods_list:物品列表  box_list:箱子列表
def greedy(goods_list,box_list):
    cmpfun = operator.attrgetter('goods_v')
    goods_list.sort(key=cmpfun, reverse=True)  # 将物品列表按体积降序排序
    i = 0 #物品列表索引（下标）
    j = 0 #箱子列表索引（下标）
    box_count = 0 #初始化箱子使用数量
    while goods_list:
        if goods_list[i].goods_v <= box_list[j].box_v:
            print('将物品:'+str(goods_list[i].goods_name)+"    装入箱子:", box_list[j].box_name)
            #更新箱子容量
            box_list[j].box_v = box_list[j].box_v - goods_list[i].goods_v
            j = 0
            del goods_list[i] #从物品列表中移除已经装入箱子的物品
        else:
            j += 1
            if box_count < j :
                box_count = j
     # 因为索引从0开始的，所以这里+1后得到箱子使用数量
    print('最终使用箱子数：',box_count+1)
    return box_list

goods_list = []
#初始化10个物品
for i in range(10):
    goods_name = "物品%s"%i
    goods_v = random.randint(1,50)
    goods_list.append(goods(goods_name,goods_v))

box_list = []
#初始化10个箱子
for i in range(10):
    box_name = "箱子%s"%i
    box_list.append(box(box_name))

box = greedy(goods_list,box_list)
print("箱子使用情况：")
for i in box:
    print(i.box_name + '  剩余容量：' + str(i.box_v))

 

（三）    示例2（0-1背包问题）

现在商店有0,1,…,n件商品，体积分别为V₀,V₁,…,V_n ,价值分别为P₀,P₁,…,P_n ，假设背包容量为V，现在要求使背包装入商品的价值最大化。

约定：

（1）   背包不足以装入所有物品。

（2）   每个商品，要么完整装入，要么放弃该商品，不能只装入商品的一部分。

算法描述：

    输入商品列表信息

    输入背包容量

    将商品列表按单位价值降序排序（就是性价比，例如：每斤值多少钱）

    while 还有商品未装入背包（或者未排除）：

        if  商品体积小等于背包剩余容量：

              将商品装入背包

              更新背包剩余容量

              在商品列表中移除已经装入背包的商品

        else：（如果背包剩余容量不足以装入商品）

              在商品列表中移除不能装入背包的商品

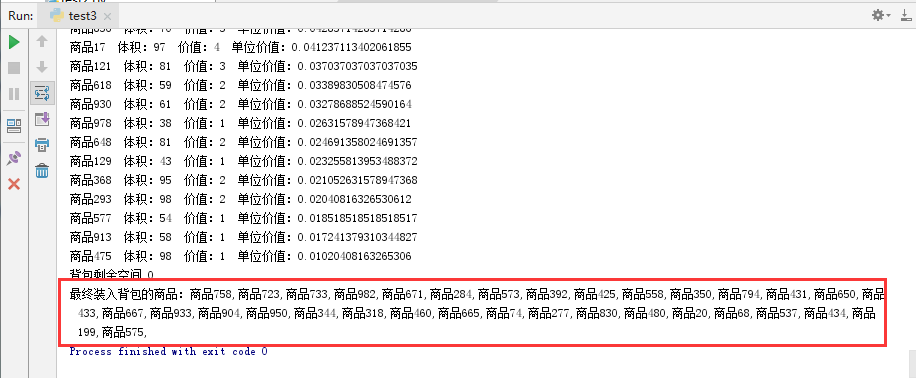
import random
import operator
#商品类
class goods():
    def __init__(self,goods_name,goods_v,goods_p):
        self.goods_name = goods_name #商品名称
        self.goods_v = goods_v   #商品体积
        self.goods_p = goods_p   #商品总价值
        self.value = self.goods_p/self.goods_v #商品单位价值

#贪心算法实现,goods_list:商品列表 V：背包剩余容量 result_list：存放最终装入背包的商品
def greedy(goods_list,V,result_list):
    cmpfun = operator.attrgetter('value')
    goods_list.sort(key=cmpfun,reverse=True) #将商品列表按单位价值降序排序
    #打印排序后的所有商品信息，这里为方便看效果，实际可以去掉这个
    for goods in goods_list:
        print(goods.goods_name +"  体积："+str(goods.goods_v)+"  价值：" + str(goods.goods_p) + "  单位价值：" +str(goods.value))
    while goods_list and V > 0:
        i = 0
        #如果商品体积小等于背包容量
        if goods_list[i].goods_v <= V:
            #将商品放入背包
            result_list.append(goods_list[i])
            #更新背包剩余容量
            V = V - goods_list[i].goods_v
            #在列表中删除该商品
            del goods_list[i]
        else:
            del goods_list[i]
    print('背包剩余空间',V)
    return result_list


V = 100 #初始化背包容量
goods_list = []
#初始化1000个商品
for i in range(1000):
    goods_name = "商品%s"%i
    goods_v = random.randint(1,100)
    goods_p = random.randint(1,100)
    goods_list.append(goods(goods_name,goods_v,goods_p))
result_list = []
result = greedy(goods_list,V,result_list)
print("最终装入背包的商品：",end='')
for i in result:
    print(i.goods_name + ",",end='')