数据结构与算法之基本概念

1. 基本概念

1.1.  什么是数据结构？

 

数据结构官方定义

• 数据结构是数据对象，以及存在于该对象的实例和组成实例的数据元素之间的各种联系。这些联系可以通过定义相关的函数来给出。——《数据结构、算法与应用》
• 数据结构是ADT（抽象数据类型Abstract Data Type）的物理实现——《数据结构与算法分析》
• 数据结构（data structure）是计算机中存储、组织数据的方式。通常情况下，精心选择的数据结构可以带来最优效率的算法。——中文维基百科

 

 

生活中的概念：

图书馆的图书如何存放？

图书馆一层层的楼层，一个个分区，一个个书架就是数据结构。

如果去存放书？存了之后又如何去取取书？这两个问题对应的就是算法。

而一本本的书籍就是我们最终的数据。

 

 

重点：

• 解决问题方法的效率，跟数据的组织方式是直接相关的
• 而现有数据量及未来预期的数据量大小，决定了组织数据的方式（数据组织形式）和细节（数据的颗粒度）

 

 

讨论1.1 对中等规模、大规模的图书摆放，你有什么更好的建议？

管理员如何存入图书？

1、为图书创建大的分类，如中文书籍，外文书籍，为每个大的分类划分一个特定区域，比如专门用一层楼存一个大的分类。

2、对大分类进行 划分一级分类，每个一级分类划分一较大的区域，然后对同一层区域进行编号，如A区至Z库

3、楼层中用大的指示牌写好这一层是哪个大分类，一层中每个大区域和小区域有提示牌这个区域是什么分类的书籍。

4、对于分类下的小分类用不同的书架，并对书架进行编号

5、书架上的图书用拼音字母A-Z进行排序和编号 

6、录入电脑系统，对分类、作者、出版年份、出版社等信息打上标记

读者/管理员如何查找图书？

1、如果读者想要查看某一类的，比如文学类的，就可以找到对应的楼层和大的分区进行图书的查阅。

2、如果读者想要找指定的图书，通过电脑去检索书籍，找到数据对应的楼层，分区，书架编号，图书编号，精准查找。

 

 

列子1.2-PrintN列子

写程序实现一个函数PrintN，使得传入一个正整数为N的参数后，能顺序打印从1到N的全部正整数。

方法1：for循环实现

 

// java代码

  public void printNForLoop(int num){

        for(int i=1;i<=num;i++){

            System.out.println(i);

        }

}

方法2：递归实现循环实现

 

    public void printNSelfLoop(int num){

        if(num>0){

            printNSelfLoop(num-1);

        }

        System.out.println(num);

    }

 

当数字num较小时两者都能较好的实现，当数字达到10万时，for循环正常打印，而递归异常了，这是因为递归占用的内存空间不够用了。

 

因此我们可以得到

解决问题方法的效率跟空间的利用效率有关。

 

 

列子 1.3 一元多项式

 

方法一：

 

  public double f1(int n,double a[],double x){

        /* 计算阶数为n，系数为a[0]...a[n]的多项式在x点的值 */

        double result = 0;

        for(int i=0; i<=n; i++){

            result += a[i] * pow(x , i);

        }

        return  result;

    }

方法二：

 

  public double f2(int n,double a[],double x){

        double result = a[n];

        for(int i=n; i>0; i--){

            result = a[i-1] + x*result;

        }

        return result;

    }

 

两个方法运行结果：

 

方法一，运行10万次耗时：115

方法二，运行10万次耗时：5

两个方法进行比较测试后，我们发现方法二比方法一好了一个数量级，因此得到解决问题方法的效率跟算法的巧妙程度有关。

 

讨论1.3 再试一个多项式

老师参与

给定另一个100阶多项式 ，用不同方法计算并且比较一下运行时间？

 

方法一：

 

public double f1(int n,double a[],double x){

    double r = a[0];

    for(int i=1; i<=n; i++){

        r += pow(x,i) / a[i];

    }

    return r;

}

 

方法二：

 

public double f2(int n,double a[],double x){

    double r = 1/a[n];

    for(int i = n-1; i >= 0; i--){

        r = 1 / a[i] + x * r;

    }

    return r;

}

两个方法运行结果：

 

方法一，运行10万次耗时：877

方法二，运行10万次耗时：50

//注意：由于除法有四舍五入的算法，到达一定位数后结果会不一致

r1:6.18737751763962

r2:6.1873775176396215

r1==r2:false

 

所以到底什么是数据结构？

• 数据对象在计算机中的组织方式
• 数据对象务必与一系列加在其上的操作相关联
• 完成这些操作所用的方法就是算法

 

抽象数据类型（Abstract Data Type）

数据类型

• 数据对象集
• 数据集合相关联的操作集

抽象：描述数据类型的方法不依赖于具体的实现

• 与存放数据的机器无关
• 与数据存储的物理结构无关
• 与实现操作的算法和编程语言均无关

 

只描述数据对象集和相关操作集“是什么”，并不涉及“如何做到”的问题

 

举个例子 ：

 

 

讨论1.4 抽象有什么好处？

• 便于找到事物之前的共同核心的特质，不必拘泥于细节
• 对一类问题定义一套规范，便于不同方法能实现同样的效果
• 讨论问题的一种通用语言，便于交流不同的思想

 

 

 

1.2. 什么是数据结构小结：

• 解决问题方法的效率，跟数据的组织方式是直接相关的
• 解决问题方法的效率跟空间的利用效率有关
• 解决问题方法的效率跟算法的巧妙程度有关
• 数据结构是数据对象在计算机中的组织方式，数据对象务必与一系列加在其上的操作相关联，完成这些操作所用的方法就是算法。
• 抽象数据类型只描述数据对象集和相关操作集“是什么”，并不涉及“如何做到”的问题

 

 

 

1.3. 什么是算法

算法的定义

算法（Algorithm）

• 一个有限指令集
• 接受一些输入（有些情况下不需要输入）
• 产生输出
• 一定在有限步骤之后终止
• 每一条指令必须

o 有充分明确的目标，不可以有歧义

o 计算机能处理的范围之内

o 描述应不依赖于任何一种计算机语言及具体的实现手段

 

 

例子1：选择排序算法的伪码描述

 

 

算法复杂度

 

 

 

 

 

以下例子使用了递归函数的他空间复杂度就是S(n)

 

 

 

 

 

 

在程序里面乘除是很耗资源的，加减可以忽略不计，

因此下面例子中的乘法数量就是一个关键

 

 

 

 

 

 

 

 

 

 

 

 

 

因为平均算法复杂度非常难以计算，因此我们分析算法的时候就是选择他的最坏的复杂度来进行分析。

1.3.1. 讨论1.5 分析“二分法”

老师参与

    查找算法中的“二分法”是这样定义的：

    给定N个从小到大排好序的整数序列List[]，以及某待查找整数X，我们的目标是找到X在List中的下标。即若有List[i]=X，则返回i；否则返回-1表示没有找到。

    二分法是先找到序列的中点List[M]，与X进行比较，若相等则返回中点下标；否则，若List[M]>X，则在左边的子系列中查找X；若List[M]<X，则在右边的子系列中查找X。

    试写出算法的伪码描述，并分析最坏、最好情况下的时间、空间复杂度。

方法一：

 

// 方法一：

// 二分法伪代码

int FindNumber(List[] list,int n,int x){

    int start = 0;

    int end = n-1;

    while(start <= end){

        /* 二分法是先找到序列的中点List[M]*/        

        int m = FindMiddle(list, start, end);

        /* list[m]与X进行比较，若相等则返回中点下标 0相等，-1小于，1大于 */

        int compare = CompareWithX(list[m], x);

        if(compare == 0){

            return  m;

        } else if ( compare == 1) {

        /* 若List[M]>X，则在左边的子系列中查找X */

            end = m + 1;

        } else if( compare == -1) {

        /* 若List[M]<X，则在右边的子系列中查找X */

            start = m + 1;

        }

    }

    return -1;

}

方法一算法复杂度分析

空间复杂度：S（1）

如果ax =N（a>0，且a≠1），那么数x叫做以a为底N的对数，记作x=log_aN，读作以a为底N的对数，其中a叫做对数的底数，N叫做真数。

最坏情况：  log2n

2的x次方等于n

2^x = n;

x  =  log₂n;

时间复杂度：T（log2n）

 

方法二：

 

// 方法二：

// 二分法伪代码

int FindNumber(List[] list,int n,int x,int start,int end){

        if(start > end){

            return -1;

        }

        /* 二分法是先找到序列的中点List[M]*/        

        int m = FindMiddle(list, start, end);

        /* m与X进行比较，若相等则返回中点下标 0相等，-1小于，1大于 */

        int compare = CompareWithX(List[m], x);

        if(compare == 0){

            return  m;

        } else if ( compare == 1) {

        /* 若List[M]>X，则在左边的子系列中查找X */

            end = m - 1;

        } else if( compare == -1) {

        /* 若List[M]<X，则在右边的子系列中查找X */

            start = m + 1;

        }

        return FindNumber(list, n, x, start, end);    

}

方法二算法复杂度分析

空间复杂度：S（n）

时间复杂度：T（log2n）

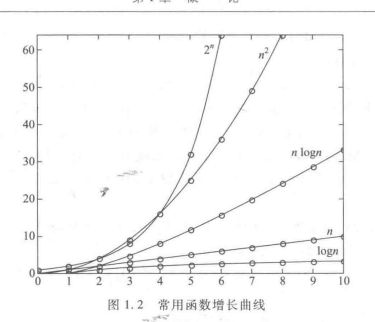
1.4. 复杂度的渐进表示法

复杂度的渐进表示法？

在比较算法优劣时，人们只考虑宏观渐进性质，即当输入规模n“充分大”时，我们观察不同复杂度的“增长趋势”，以判断那种算法必定效率更高。

 

 

 

 

 

 

 

 

 

 

 

 

这里的上界暂且理解为最好的情况，下界理解为最坏的情况。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.5. 应用实例：最大子列和

 

 

 

 

算法1

 

 

 

空间复杂度：O(1)

时间复杂度：O(n³)

 

 

 

 

空间复杂度：O(1)

时间复杂度：O(n²)

算法2是解决了算法1每次都 从0开始计算的弊病，直接从j-1次循环的结果上累加就好

 

算法3：分而治之

 

 

 

算法实现举例：

 

 

 

 

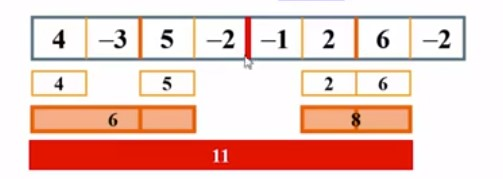
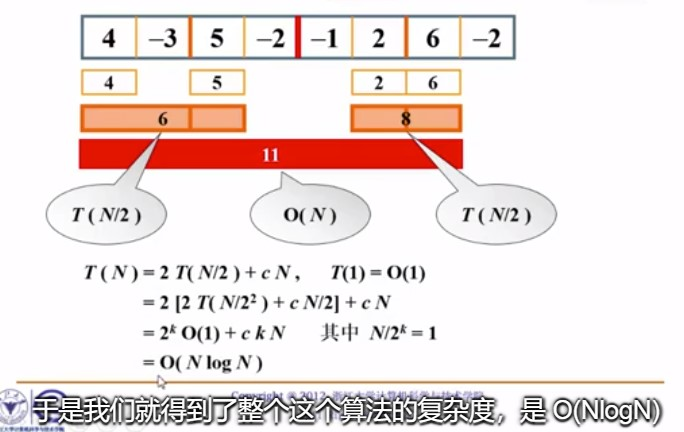
算法复杂度分析：

 

 

 

 

 

import java.util.ArrayList;

import java.util.List;

public class t {

    public static void main(String[] args) {

        int arr[] = new int[]{4, -3, 5, -2, -1, 2, 6, -2};

        int r = new t().MaxSubseqSum3(arr, 8);

    }

 int Max3( int A, int B, int C )

{ /* 返回3个整数中的最大值 */

    return A > B ? A > C ? A : C : B > C ? B : C;

}

int DivideAndConquer(int[] List, int left, int right )

{ /* 分治法求List[left]到List[right]的最大子列和 */

    int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */

    int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/

    int LeftBorderSum, RightBorderSum;

    int center, i;

    if( left == right )  { /* 递归的终止条件，子列只有1个数字 */

        if( List[left] > 0 )  return List[left];

        else return 0;

    }

    /* 下面是"分"的过程 */

    center = ( left + right ) / 2; /* 找到中分点 */

    /* 递归求得两边子列的最大和 */

    MaxLeftSum = DivideAndConquer( List, left, center );

    MaxRightSum = DivideAndConquer( List, center+1, right );

    /* 下面求跨分界线的最大子列和 */

    MaxLeftBorderSum = 0; LeftBorderSum = 0;

    for( i=center; i>=left; i-- ) { /* 从中线向左扫描 */

        LeftBorderSum += List[i];

        if( LeftBorderSum > MaxLeftBorderSum )

            MaxLeftBorderSum = LeftBorderSum;

    } /* 左边扫描结束 */

    MaxRightBorderSum = 0; RightBorderSum = 0;

    for( i=center+1; i<=right; i++ ) { /* 从中线向右扫描 */

        RightBorderSum += List[i];

        if( RightBorderSum > MaxRightBorderSum )

            MaxRightBorderSum = RightBorderSum;

    } /* 右边扫描结束 */

    /* 下面返回"治"的结果 */

    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );

}

int MaxSubseqSum3(int[] List, int N )

{ /* 保持与前2种算法相同的函数接口 */

    return DivideAndConquer( List, 0, N-1 );

}

}

 

 

 

 

 

 

这个算法的特点是无论我们停在中间的哪一步，返回的最大子列和都是当前输入数据的正确解。图示如下：

 

 

 

 

 

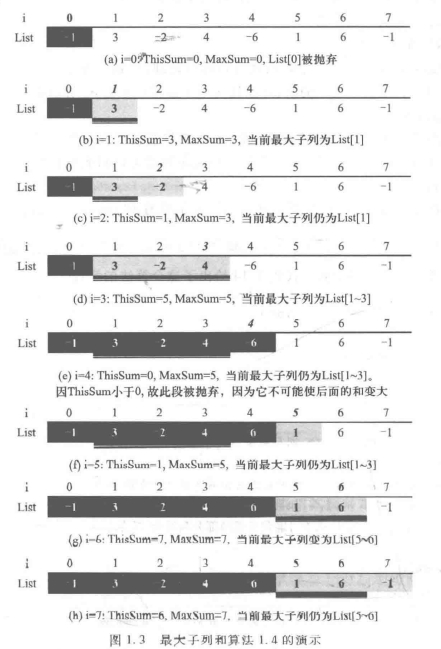
由此可以得到提高效率的窍门之一，是让计算机“记住”一些关键的中间结果，避免重复计算。

 

1.6. 本章小结

本章介绍了两个重要的概念“数据结构”和“算法”。

 

“数据结构”包括数据对象集以及他们在计算机中的组织方式，即他们的逻辑结构和物理存储结构，同时还包括与数据对象集相关联的操作集，以及实现这些操作的最高效的算法。

抽象数据类型是用来描述数据结构的重要工具。

“算法”是解决问题步骤的有限集合，通常用某一计算机语言进行伪码描述。我们用时间复杂度和空间复杂度来衡量算法的优劣，用渐进表示法分析算法复杂度的增长趋势。