最大子列和的四种方法，时间复杂度递减，直至为线性复杂度

三个for循环，时间复杂度为N的立方。

下面是我跟着老师的思路打的代码，

#include<stdio.h>
int f(int a[],int n) {
    int i,j,k;
    int res=0;;
    for(i=0; i<n; i++) {    //i是开始位置
        for(j=i; j<n; j++) {    //j是结束位置
            int max=0;
            for(k=i; k<=j; k++) {
                max+=a[k];
            }
//            printf("max=%d\n res=%d",max,res);
            if(max>=res) {
                res=max;
            }
        }

    }
    return res; 
}

int main() {
    printf("hello\n");
    int a[]= {1,2,3,4,5} ;
    int n=5;
    int s=f(a,n);
    printf("s=%d",s);
    return 0;
}

改进后的

#include<stdio.h>
int f(int a[],int n){
    int i,j;
    int ThisSum=0,MaxSum=0;
    for(int i=0;i<n;i++){    //i是子列左端的位置 
            ThisSum=0;        //ThisSum是子列的和 
        for(int j=i;j<n;j++){    //j是子列右端的位置 
                ThisSum+=a[j];
                if(ThisSum>MaxSum){
                    MaxSum=ThisSum;
                }
        }
    }
    
    return MaxSum;
}

int main(){
    //数组和大小自己手动更改 
    int a[]={1,2,3,-4,0,5};
    int n=6;
    int res=f(a,n);
    printf("res=%d",res);
    
    return 0;
}

这下时间复杂度是N的平方。

老师前面也讲过，时间复杂度为n的平方，本能的应该想把它降为nlogn

下面的分治算法就可以做到

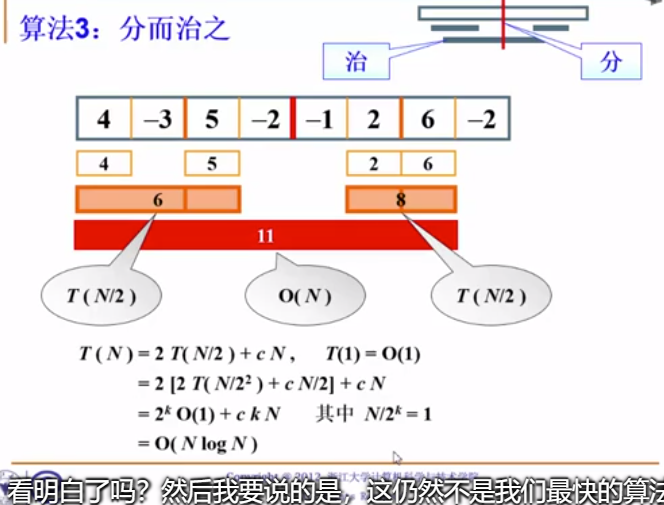
大题思想是把它看成三个部分，左边、右边、中间，也就是分、分、治。

代码还需要去找找，找到了自己熟悉了再贴出来

下面的算法就是最简单的了，老师说的它的名字叫在线处理

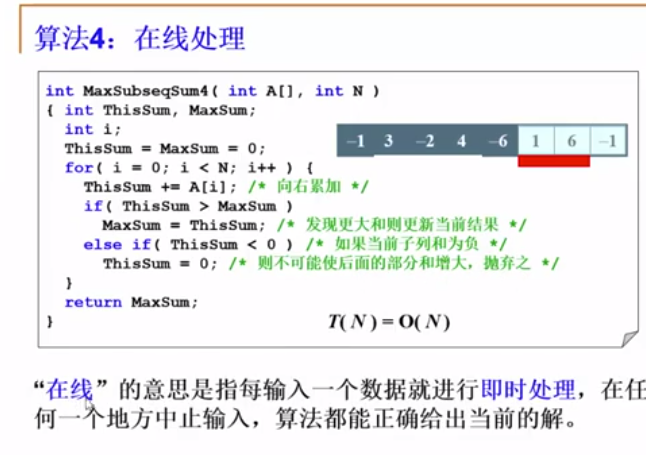
下面是代码。