我要翻译《Think Python》- 006 第四章 学习案例:接口设计
本文翻自:Allen B. Downey ——《Think Python》
原文链接:http://www.greenteapress.com/thinkpython/html/thinkpython005.html
翻译:Simba Gu
[自述:感觉从这一章开始算是有点“干货”了,很容易激起初学者的兴趣,想当年上学的时候就是老师随便写的一个循环语句让两个大于号“>>”沿着屏幕绕圈就像贪吃蛇一样,吸引了我并且让我入了写程序这个“坑”]
第四章
学习案例:接口设计
本章示例代码可以从这里下载:
http://thinkpython.com/code/polygon.py
4.1 TurtleWorld
为了配合本书,我写了一个Swampy包,你可以从这里下载并按照上面的说明安装到你的系统:http://thinkpython.com/swampy
包是一个模块的集合,TurtleWorld就是Swampy里面的一个模块,它提供了一些引导小海龟在屏幕上画线的函数集。你只要在系统中安装了Swampy包就可以导入TurtleWorld模块:
from swampy.TurtleWorld import *
如果你下载了Swampy包,但是没有安装,你可以在Swampy的根目录调试程序,或者把该目录添加到Python可以搜索的路径中去,然后再这样导入TurtleWorldlike :
from TurtleWorld import *
安装过程和Python搜索路径的设置,取决于你的系统,本书就不作具体描述,如有疑问请参考此链接:http://thinkpython.com/swampy
建立一个文件mypolygon.py,输入下面的代码:
from swampy.TurtleWorld import * world = TurtleWorld() bob = Turtle() print bob wait_for_user()
第一行代码表示从swampy包导入TurtleWorld 模块。接下来一行建立一个TurtleWorld 对象和Turtle对象分别赋值给变量world和bob。打印bob变量你会看到类似这样的结果:
<TurtleWorld.Turtle instance at 0xb7bfbf4c>
这表示bob变量引用了TurtleWorld 模块的一个实例 Turtle。从上下文中可以看出,“实例”表示集合的一个成员,这里的Turtle实例可以是一组或者集合中的一个。
这里的 wait_for_user 告诉TurtleWorld 等待用户下一步操作,尽管在这个案例中除了等用户关闭窗口之外并无其它。
TurtleWorld 提供了一些turtle转向的函数:fd和bk用于前进和后退,lt和rt用于左右转弯。并且每一个Turtle对象都有一支“笔”,可以落下或提起,如果笔落下,当Turtle对象移动的时候就会留下痕迹。函数pu和pd分别表示“提笔”和“落笔”。
下面的代码可以画一个直角(代码放在建立的bob对象和 wait_for_user 函数之间):
fd(bob, 100)
lt(bob)
fd(bob, 100)
第一行代码让bob向前移动100,第二行让它向左转弯。当你运行程序的时候,你就可以看到bob向东向北移动并留下了运行轨迹。
请修改代码画一个正方形。在实现此功能之前请不要继续本章内容!
4.2 简单循环
你可能写了这样的代码(此处省略了建立TurtleWorld 对象和调用wait_for_user 函数)
fd(bob, 100) lt(bob) fd(bob, 100) lt(bob) fd(bob, 100) lt(bob) fd(bob, 100)
我们还可以用for循环语句来实现重复的功能。请添加以下代码到mypolygon.py脚本文件并运行:
for i in range(4): print 'Hello!'
你应该可以看到下面的结果:
Hello!
Hello!
Hello!
Hello!
这个例子里面用到了for语句,后面我们还会看到更多。但是这足以让你重新编写画正方形的程序,下面就是for语句实现的代码:
for i in range(4): fd(bob, 100) lt(bob)
for语句的语法类似函数定义,它有一个以冒号结尾的头和缩进的正文,正文内可以包含任意数量的语句。
for语句有时被称为循环,因为执行流程经过正文处理之后又回到循环的顶部。在这个案例中,正文内容被执行了4次。
这里的代码跟之前画正方形的代码有些不同,因为在画出了正方形之后又进行了一次转弯,这样会花费额外的处理时间,但是如果是重复的动作,这样会简化代码,而且for循环的这个版本让Turtle回到原点之后也恢复了初始的方向。
4.3 练习
下面是TurtleWorld系列的一些练习,这些本来是为了好玩,但是其中也不乏一些编程思想。当你在练习的时候请思考一下重点是什么。
本书提供了下面练习的解决方案,你可以先尝试一下,不要直接抄答案。
1. 编写一个名为square的函数,它传递一个名为 t 的turtle对象参数,实现用turtle对象画一个正方形。编写一个函数调用,将bob作为参数传递给square,然后再次运行程序。
2. 在square函数添加另一个名为length的参数。修改函数内容,实现所画正方形的边长度为length,然后修改函数调用,加入第二个参数,再次运行程序。使用一定长度范围的值来测试程序。
3. 默认情况下,lt和rt函数进行90度旋转,但您可以提供第二个参数,指定角度的数量。例如,lt(bob, 45) 可以让bob向左旋转45度。复制一个square函数,把它的名字改成polygon。再添加另一个名为n的参数并修改polygon函数主体,使其绘制一个n边正多边形。提示:n边正多边形的外角是360/n 度。
4. 编写一个名为circle的函数,该函数以turtle对象 t 和半径 r 为参数,通过调用具有适当长度和边数的多边形来绘制一个近似圆。用一定范围的 r 来测试函数。
-
-
- 提示:求出圆的周长,确保 length * n = circumference。
- 另一个提示:如果你觉得 bob 速度太慢,你可以通过改变bob.delay(移动间隔时间)来加快速度,以秒为单位,例如 bob.delay = 0.01。
-
5. 制作一个更通用的circle 函数,添加一个额外的参数angle,用来决定画一个圆弧的哪个部分。以angle为单位,当angle=360时,circle 函数就会画一个完整的圆。
4.4 封装
上文中的第一个练习要求将画正方形图形的代码放入函数定义中,然后调用函数,并将turtle作为参数传递。解决方案如下:
def square(t): for i in range(4): fd(t, 100) lt(t) square(bob)
在最内层的语句,fd 和 lt 缩进两次以表名它们位于for循环中,而for循环位于函数定义中。函数调用行square(bob)与左侧空白齐平,因此这是for循环和函数定义的结尾。
在函数内部,t 表示Turtle对象bob,因此 lt(t) 与 lt(bob) 具有相同的效果。那这里为什么不直接调用参数bob呢?这是因为这里的 t 可以是任何Turtle对象,而不仅仅是bob,因为你可以创建另一个Turtle对象并将它作为参数传递给square函数:
ray = Turtle()
square(ray)
在函数中包装一段代码称为封装。封装的好处之一是它可以将一个名称附加到代码上,作为一种文档。另一个优点是,如果重用代码,调用函数两次比复制和粘贴主体更简单方便!
4.5 泛化
接下来是给square函数添加一个参数length。实现代码如下:
def square(t, length): for i in range(4): fd(t, length) lt(t) square(bob, 100)
向函数添加参数称为泛化,因为它使函数更通用:在以前的版本中,正方形的大小是相同的;在这个版本中,它可以是可变的。
下一步也是泛化。polygon 函数是画出任意数量的正多边形,而不是正方形。实现代码如下:
def polygon(t, n, length): angle = 360.0 / n for i in range(n): fd(t, length) lt(t, angle) polygon(bob, 7, 70)
这段代码将绘制一个边长度为70的7边形。如果函数有多个数值参数,那将会很容易忘记它们是什么,或者它们应该处于什么顺序。在参数列表中包含参数的名称是合法的,有时是很有帮助的:
polygon(bob, n=7, length=70)
这些被称为关键字参数,因为它们包含参数名作为“关键字”(不要与Python关键字,如while和def等混淆)。
这种语法使程序更具可读性,还提醒了参数和参数是如何工作的:当您调用一个函数时,实参数被分配给形参。
4.6 接口设计
下一步就是写以半径 r 为参数的circle函数。这里有一个简单的解决方案,就是用polygon 函数画一个50面的多边形。
def circle(t, r): circumference = 2 * math.pi * r n = 50 length = circumference / n polygon(t, n, length)
第一行计算圆的周长,公式为2π*r。因为我们使用到了pi值,所以需要导入math模块。按照惯例,通常import语句都位于脚本的开头。
n是画一个圆需要的近似的线的段数,所以length是每个线段的长度。因此,polygon 函数绘制了一个50边的多边形,它近似于一个半径为 r 的圆。
这个解决方案有一个限制就是 n 是常数,这意味着对于很大的圆,每一个线段太长,对于小的圆来说又浪费时间画很小的线段。因此,一个解决方案是把n作为参数来泛化这个函数。这将给用户(无论谁调用circle函数)更多的控制,但界面将会变得有些乱。
函数的接口是如何使用它:参数是什么?函数可以做什么?返回值是多少?如果接口“尽可能简单,但不简单”,那么它就是“精炼”的。(爱因斯坦)
在本例中,变量 r 属于接口,因为它指定了要绘制的圆。n 则不是,因为它是函数内部如何渲染圆的局部变量。
因此,与其让界面混乱,还不如根据周长选择合适的 n 的值:
def circle(t, r): circumference = 2 * math.pi * r n = int(circumference / 3) + 1 length = circumference / n polygon(t, n, length)
现在画线的段数是(大约)circumference/3,所以每个段的长度是(大约)3,每一段线的长度足够小,这样画出来的圆看起来才平滑,只要线的段数大到足够有效,就可以画出任何大小的圆。
4.7 重构
当我在写circle函数的时候我可以重用polygon函数,应为一个许多边的多边形就是一个近似的圆。但是圆弧却不能重用circle和polygon函数。
有一个可选的方法就是复制一份polygon函数,再改成 arc 函数。改完之后大致如下:
def arc(t, r, angle): arc_length = 2 * math.pi * r * angle / 360 n = int(arc_length / 3) + 1 step_length = arc_length / n step_angle = float(angle) / n for i in range(n): fd(t, step_length) lt(t, step_angle)
这个函数的后半部分看起来像polygon函数,但是我们不能在不改变接口的情况下重用polygon函数。我们可以泛化polygon函数以一个角度作为第三个参数,但polygon将不再是一个合适的函数名字! 我们可以用一个更通用的函数名称polyline:
def polyline(t, n, length, angle): for i in range(n): fd(t, length) lt(t, angle)
因此可以把polyline函数重新改写polygon函数和arc 函数:
def polygon(t, n, length): angle = 360.0 / n polyline(t, n, length, angle) def arc(t, r, angle): arc_length = 2 * math.pi * r * angle / 360 n = int(arc_length / 3) + 1 step_length = arc_length / n step_angle = float(angle) / n polyline(t, n, step_length, step_angle)
最后,我们可以用arc函数重写circle函数:
def circle(t, r): arc(t, r, 360)
这个过程——重新安排程序以改进功能接口并促进代码重用可以称为“重构”。在本例中,我们注意到在arc和polygon函数中有类似的代码,因此我们将其分解为polyline函数。
如果我们提前规划代码,我们可能会首先编写polyline函数并避免重构,但通常在项目开始的时候,您对程序设计中所需要的接口还不够了解。只有在开始编写代码之后,您才会更好地理解问题。某种程度上来说,当你开始重构的函数的时候标志着你已经学会了一些东西了。
4.8 开发方案
开发计划是一个编写程序的过程。我们在本案例研究中使用的过程是“封装和泛化”。这项工作的步骤如下:
首先编写一个没有函数定义的小程序。
一旦程序可以正常运行,再把它封装在一个函数中,并且给函数起个名字。
通过添加适当的参数来拓展该函数。
重复步骤1–3,直到你有一个函数的集合。复制并粘贴工作代码,以避免重复输入(和重新调试)。
通过重构寻找改进程序的机会。例如,如果您在几个地方有类似的代码,考虑将其分解为适当的通用函数。
这个过程是有一些缺点的——我们在本书的后面会有替代方案——如果你不知道如何将程序划分为函数,这也不影响你继续本书的学习。
4.9 文档字符串
docstring是函数开头的一个字符串,用于解释接口(“doc”是“documentation”的缩写)。这里有一个例子:
def polyline(t, n, length, angle): """Draws n line segments with the given length and angle (in degrees) between them. t is a turtle. """ for i in range(n): fd(t, length) lt(t, angle)
这个docstring是一个用三引号括起来的字符串,也称为多行字符串,因为三元引号允许字符串跨越多行。
它很简洁,但是它包含了一些函数所需要的重要信息。它简明地解释了函数的作用(没有详细介绍它是如何完成的)。它解释了每个参数对函数行为的影响,以及每个参数应该是什么类型(如果不是很明显的话)。
编写这种文档是接口设计的一个重要部分。设计良好的接口应该很容易解释;如果您在解释您的某个函数时遇到了困难,这意味着这个接口还可以再改进。
4.10 调试
接口就像函数和调用者之间的契约。调用方同意提供某些参数,该函数同意执行某些工作。
例如,polyline 函数需要四个参数:t 必须是Turtle对象,n是线段的数目,所以n必须是一个整数;length应该是一个正数;angle必须是一个数字,表示角度的意思。
这些需求被称为先决条件,因为它们应该在函数开始执行之前准备好。相反,函数末尾的条件是后置条件。后置条件包括函数的预期效果(比如画线段)和任何副加作用(如移动Turtle或在TurtleWorld中进行其他修改)。
先决条件是调用方的责任。如果调用方违反了一个(适当的文档化的)先决条件,并且函数不能正常工作,那问题就在函数调用的地方,而不是函数里面。
4.11 术语表
实例:
一个集合中的成员。本章中的TurtleWorld是TurtleWorld集合的成员。
循环:
程序中可以重复执行的部分。
封装:
将语句序列转换为函数定义的过程。
概括:
用适当的通用(如变量或参数)替换不必要的特定对象(如数字)的过程。
关键参数:
包含参数名称作为“关键字”的参数。
接口:
描述如何使用一个函数,包括参数的名称和描述以及返回值。
重构:
修改工作程序的过程,以改进函数接口和代码的其他质量。
开发计划:
编写程序的过程。
文档字符串:
在函数定义中显示的用于记录函数接口的字符串。
先决条件:
函数启动前调用方应该满足的需求。
后置条件:
函数结束前应该满足的需求。
4.12 练习
练习 1
从http://thinkpython.com/code/polygon.py下载本章下载本章中的代码。
为polygon、arc 和circle函数编写适当的文档。
绘制一个堆栈图,显示执行圆时程序的状态(bob,radius)。您可以手工进行算术或向代码中添加打印语句。
第4.7节中弧的版本不是很精确,因为圆的线性近似总是在真圆之外。因此导致Turtle离正确的目的地还差了几个单位。我给出的解决方案减小此错误影响的方法。请阅读代码,看看它对您是否有意义。如果你画一个图表,你可能会看清除它是如何工作的。

图4.1
练习 2
编写一组适当的通用函数,可以绘制如图4.1所示的图案。
解决方案:
http://thinkpython.com/code/flor.py
http://thinkpython.com/code/polygon.py
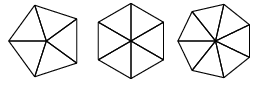
图4.2
练习 3
编写一组适当的通用函数,可以绘制如图4.2所示的形状。
解决方案:http://thinkpython.com/code/pie.py
练习 4
字母表中的字母可以用一定数量的基本元素构成,如垂直线和水平线以及一些曲线。设计一种字体,它可以用最少的基本元素绘制,然后编写绘制字母的函数。
您需要为每个字母编写一个函数,并命名为draw_a, draw_b, ...等,并将您的函数放入名为letters.py 的文件。你可以从可以从 http://thinkpython.com/code/typewriter.py 下载一个下载一个“Turtle打字机”来帮助你测试你的代码。
解决方案:
http://thinkpython.com/code/letters.py
http://thinkpython.com/code/polygon.py
练习 5
请阅读请阅读 http://en.wikipedia.org/wiki/Spiral 上的相关文章;然后编写一个绘制阿基米德螺旋(或其他种类的程序)
解决方案:
http://thinkpython.com/code/spiral.py.
#英文版权 Allen B. Downey #翻译中文版权 Simba Gu #转载请注明出处


 浙公网安备 33010602011771号
浙公网安备 33010602011771号