A*查找迷宫最佳路径

1 准备工作

1.1 地图

\[\begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{bmatrix} \]

其中0表示路，1表示障碍，起点在(0,0)，终点在(4,4)

那么得到的路径应该是：

\[\begin{bmatrix} \textbf{A} & \textbf{B} & 0 & 0 & 0 \\ 1 & \textbf{C} & 1 & 0 & 1 \\ \textbf{E} & \textbf{D} & 1 & 1 & 1 \\ \textbf{F} & 1 & \textbf{J} & \textbf{K} & \textbf{L} \\ \textbf{G} & \textbf{H} & \textbf{I} & 1 & \textbf{M} \end{bmatrix} \]

路径是：
(0, 0) -> (0, 1) -> (1, 1) -> (2, 1) -> (2, 0) -> (3, 0) ->
(4, 0) -> (4, 1) -> (4, 2) -> (3, 2) -> (3, 3) -> (3, 4) -> (4, 4)

1.2 一点代码

1.2.1 优先队列

因为A^*算法每次需要找到代价最低的节点，然后进行探测。所以这里使用最小堆来维护Open表

import heapq

class PriorityQueue:
    def __init__(self):
        self._queue = []
        self._index = 0

    def push(self, item, priority):
        """
        队列由 (priority, index, item) 形式组成
        index 是为了当两个对象的优先级一致时，按照插入顺序排列
        """
        heapq.heappush(self._queue, (priority, self._index, item))
        self._index += 1

    def pop(self):
        return heapq.heappop(self._queue)[-1]

    def empty(self):
        return True if not self._queue else False

    def __len__(self):
        return self.qsize()

1.2.2 地图类

class GameMap:
    def __init__(self):
        self.game_map = None
        self.rows = 0
        self.cols = 0

    def static_map(self):
        self.game_map = [
                [0, 0, 0, 0, 0],
                [1, 0, 1, 0, 1],
                [0, 0, 1, 1, 1],
                [0, 1, 0, 0, 0],
                [0, 0, 0, 1, 0]
            ]
        self.rows = self.cols = 5

    def is_obstacles(self, row: int, col: int) -> bool:
        # 判断该点是否是障碍物
        return self.game_map[row][col] == 1

1.2.3 节点类

该节点类的对象会保存到Open表中。关于如何保存最佳路径，这里采用的方式是让节点记住它的父节点。比如，当探测到终点后，我们从重点开始向前递归，不断递归父节点father，从而还原出整条路径。

from typing import Tuple


class Node:
    def __init__(self, point: Tuple[int, int], g, h, father=None):
        self.point = point  # 坐标
        self.father = father  # 父节点, 用于生成路径使用
        self.g = g  # 实际代价
        self.h = h  # 未来代价
        self.f = g + h  # 总代价

    def __eq__(self, __o: object) -> bool:
        return __o.point == self.point

2 AStar

这里提供曼哈顿距离和欧式距离作为启发式函数

from typing import Tuple
import time
import math
from collections import defaultdict

class AStar:
    def __init__(self, game_map: GameMap, start: Tuple[int, int], end: Tuple[int, int]):
        # 进行一些检查, 起始点和结束位置不能是障碍物
        assert len(start) == len(end) == 2
        assert not game_map.is_obstacles(*start)
        assert not game_map.is_obstacles(*end)
        self.game_map = game_map
        self.start = start
        self.end = end
        self.open_table = PriorityQueue()
        self.close_table = defaultdict(set)
        # 定义的行进方向
        self.direction = ((-1, 0), (1, 0), (0, -1), (0, 1))
        # 存储最短路劲
        self.path = []
        # 设置启发式函数
        self.h_method = {
            0: AStar.manhattan,
            1: AStar.euclidean
        }
        # 记录一些状态
        self.record = {
            'open_size': [],
            'close_size': []
        }

    @staticmethod
    def manhattan(start: Tuple[int, int], end: Tuple[int, int]):
        return abs(start[0] - end[0]) + abs(start[1] - end[1])

    @staticmethod
    def euclidean(start: Tuple[int, int], end: Tuple[int, int]):
        dx = start[0] - end[0]
        dy = start[1] - end[1]
        return math.sqrt(dx ** 2 + dy ** 2)

    def find_path(self, h_method_no: int = 0) -> None:
        # 初始化
        t1 = time.perf_counter()
        hm = self.h_method
        self.path = []
        node = Node(self.start, 0, hm[h_method_no](self.start, self.end))
        self.open_table.push(node, node.f)

        flag = True
        target = None
        while flag:
            # 从open表中获取代价最小的点
            chosen_node: Node = self.open_table.pop()
            cx, cy = chosen_node.point
            # 以该节点为基准, 探测周围四步
            for dx, dy in self.direction:
                fx, fy = cx + dx, cy + dy
                # 没有超出地图边界
                if 0 <= fx < self.game_map.rows and 0 <= fy < self.game_map.cols:
                    # 判断探测到的位置是否在close表中
                    if fy in self.close_table[fx]:
                        continue
                    # 判断是否是障碍物
                    if self.game_map.is_obstacles(fx, fy):
                        continue
                    # 创建新节点, 并加入到open中
                    new_node = Node(point=(fx, fy),
                                    g=chosen_node.g + 1,
                                    h=hm[h_method_no](self.start, self.end),
                                    father=chosen_node)

                    # 如果探测到终点
                    if (fx, fy) == self.end:
                        target = new_node
                        flag = False
                        break
                    self.open_table.push(new_node, new_node.f)

            # 当前节点关闭
            self.close_table[cx].add(cy)

            # 记录
            self.record['open_size'].append(len(self.open_table))
            self.record['close_size'].append(sum(len(v) for v in self.close_table.values()))

            if self.open_table.empty():
                flag = False
        t2 = time.perf_counter()
        self.record['time'] = f'{t2 - t1}'
        if target is None:
            print(f'No available path from start:{self.start} to end: {self.end}')
        else:
            self.get_path(target)
            self.path.reverse()

    def get_path(self, node: Node) -> None:
        if node is None:
            return
        self.path.append(node.point)
        self.get_path(node.father)

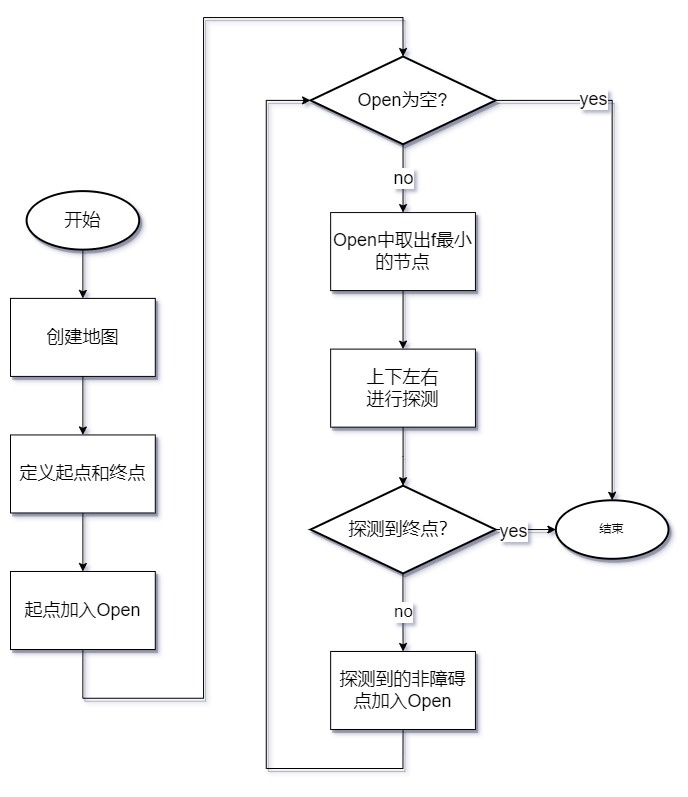
3 测试

if __name__ == '__main__':
    # 创建地图
    game_map = GameMap()
    game_map.static_map()
    start, end = (0, 0), (4, 4)
    # 创建算法对象
    astar = AStar(game_map, start, end)
    # 这里测试曼哈顿距离作为启发式函数
    astar.find_path(0)
    print(astar.path)
    print(max(astar.record['time']))
    print(max(astar.record['open_size']))
    print(max(astar.record['close_size']))

测试结果得到路径与前文一致。