20172312 2018-2019-1 《程序设计与数据结构》第九周学习总结
教材学习内容总结
第十五章
图
无向图
1.图是由结点和这些结点之间的连接所构成,结点叫做顶点,结点之间的连接是边,树是图的一种。
2.无序图是一种边为无序结点对的图,如果图中的两个顶点之间有一条连通边,则称为这两个顶点是邻接的,邻接顶点有时也称为邻居,连通一个顶点及其自身的边称为自循环或环。
3.路径是图中的一系列边,路径的长度是该路径中边的条数(或顶点数减1)。
4.若一个无向图含有最多条边,那么它为完全图。对于有n个顶点的无向图,第x个顶点,需要(n-x)条边将其与其他顶点联通,有n(n-1)/2条边。
5.若无向图中任意两个顶点之间都存在一条路径,那么认为这个无向图是连通的。
有向图
1.有向图也称为双向图,它是一种边为有序顶点对的图,有向图中的路径是图中连通两个顶点的有向边序列。
2.如果有向图中没有环路,且有一条从A到B的边,则可以把顶点A安排在顶点B之前,这种排列得到的顶点次序称为拓扑序。
3.可以使用某一队列列表(其中每一队列都表示了给定优先级的项目)来实现一个优先级队列
4.按照优先级对堆排序完成了第一次排序(高优先级的项目在先)。但是,我们必须对具有相同优先级项目的先进先出排序进行操纵:
解决方案是创建一个 PriorityQueueNode对象,它存储的是将被放置在队列中的元素,该元素的优先级,以及元素放进队列的顺序
然后,我们只需为 PriorityNode类定义个 compareTo方法,以便先对优先级进行比较,然后在优先级一样的时候再对阶进行比较
网络
1.网络或称加权图,是一种每条边都带有权重或代价的图,加权图中的路径权重是该路径中各条边权重的和。
2.对于网络,我们将用一个三元组来表示每条边,这个三元组中包括起始顶点、终止顶点和权重。
3.对于无向网络来说,起始顶点与终止顶点可以互换。
常用图算法
遍历
1.广度优先遍历(队列实现):首先,从图的某个顶点v0出发,访问了v0之后,依次访问与v0相邻的未被访问的顶点,然后分别从这些顶点出发,广度优先遍历,直至所有的顶点都被访问完。
- (1)从一个未走到过的顶点作为起始顶点,比如元素0顶点作为起点。
- (2)沿0顶点的边去尝试访问其它未走到过的顶点,首先发现2顶点还没有走到过,于是来到了2顶点。
- (3)返回到0顶点,再以0顶点作为出发点继续尝试访问其它未走到过的顶点,这样来到了1顶点。
- (4)返回到0顶点,再以0顶点作为出发点继续尝试访问其它未走到过的顶点,这样来到了5顶点。
- (5)此时沿0顶点的边,已经不能访问到其它未走到过的顶点了,所以需要返回到2顶点。
- (6)沿2顶点的边去尝试访问其它未走到过的顶点,(因为1顶点已经走过了)首先发现3顶点还没有走到过,于是来到了3顶点。
- (7)返回到2顶点,再以2顶点作为出发点继续尝试访问其它未走到过的顶点,这样来到了4顶点。
- (8)此时沿4顶点的边,已经不能访问到其它未走到过的顶点了,至此,所有顶点我们都走到过了,遍历结束。
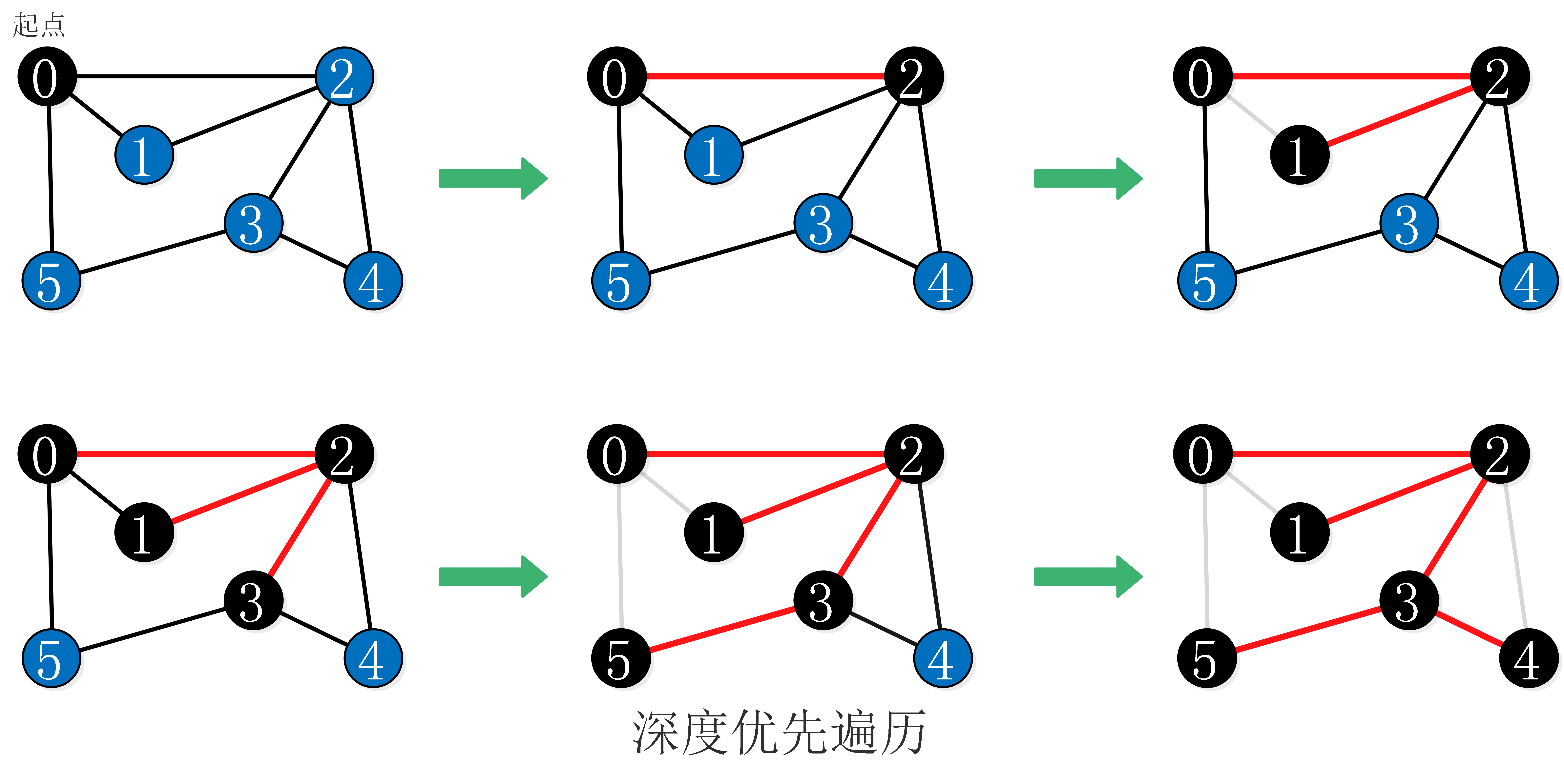
2.深度优先遍历(栈实现):首先从图中某个顶点v0出发,访问此顶点,然后依次从v相邻的顶点出发深度优先遍历,直至图中所有与v路径相通的顶点都被访问了;若此时尚有顶点未被访问,则从中选一个顶点作为起始点,重复上述过程,直到所有的顶点都被访问。在访问某一个顶点时:将它标为已访问,递归的访问它的所有未被标记过的邻接点
- (1)首先从一个未走到过的顶点作为起始顶点,比如元素0顶点作为起点。
- (2)沿0顶点的边去尝试访问其它未走到过的顶点,首先发现2顶点还没有走到过,于是来到了2顶点。
- (3)再以2顶点作为出发点继续尝试访问其它未走到过的顶点,这样又来到了1顶点。
- (4)再以1号顶点作为出发点继续尝试访问其它未走到过的顶点。
- (5)此时沿1顶点的边,已经不能访问到其它未走到过的顶点了,所以需要返回到2顶点。
- (6)返回到2号顶点后,以2顶点作为出发点继续尝试访问其它未走到过的顶点,此时又会来到3顶点,再以3号顶点作为出发点继续访问其它未走到过的顶点,于是又来到了5号顶点。
- (7)此时沿5顶点的边,已经不能访问到其它未走到过的顶点了,所以需要返回到3顶点。
- (8)返回到3顶点后,以3顶点作为出发点继续尝试访问其它未走到过的顶点,此时会来到4顶点,再以4顶点作为出发点继续访问其它未走到过的顶点。
- (9)此时沿4顶点的边,已经不能访问到其它未走到过的顶点了,至此,所有顶点我们都走到过了,遍历结束。
图算法
1.测试连通性:在一个图中,无论哪个为起始顶点,当且仅当广度优先遍历中的顶点数等于图中的顶点数目时,则该图是连通的。
2.最小生成树:
- 生成树是一棵含有图中所有顶点和部分边(可能不是所有边)的树。
- 最小生成树是边的权重总和和小于或等于同一个图中其他任何一棵生成树的权重总和。
- 非连通的无向图,不存在最小生成树
- 权重不一定和距离成正比
- 权重可能是0或负数
- 若存在相等的权重,那么最小生成树可能不唯一
3.判断最短路径:
- 方法一:判定起始顶点与目标顶点之间的字面意义上的最短路径,即两个顶点之间的最小边数。
- 方法二:在加权图途中,寻找加权图的最便宜路径即为最短路径。
图的实现
1.邻接列表
- 在邻接表的表示中,无向图的同一条边在邻接表中存储的两次。如果想要知道顶点的读,只需要求出所对应链表的结点个数即可。
- 有向图中每条边在邻接表中只出现一此,求顶点的出度只需要遍历所对应链表即可。求出度则需要遍历其他顶点的链表。
2.邻接矩阵:
- 在邻接矩阵表示中,无向图的邻接矩阵是对称的。矩阵中第 i 行或 第 i 列有效元素个数之和就是顶点的度。
- 在有向图中 第 i 行有效元素个数之和是顶点的出度,第 i 列有效元素个数之和是顶点的入度。
3.邻接矩阵与邻接表优缺点:
- 邻接矩阵的优点是可以快速判断两个顶点之间是否存在边,可以快速添加边或者删除边。而其缺点是如果顶点之间的边比较少,会比较浪费空间。因为是一个 n∗nn∗n 的矩阵。而邻接表的优点是节省空间,只存储实际存在的边。其缺点是关注顶点的度时,就可能需要遍历一个链表。还有一个缺点是,对于无向图,如果需要删除一条边,就需要在两个链表上查找并删除。
4.边集数组:
- 边集数组由两个一维数组构成:一个存储顶点信息; 一个存储边的信息,这个边数组每个数据元素由一条边的起点下标、终点下标、和权组成。
- 边集数组关注的是边的集合,在边集数组中要查找一个顶点的度需要扫描整个边数组,效率并不高。因此它更适合对边依次进行处理的操作,而不适合对顶点相关的操作。
5.十字链表:
- 十字链表是为了便于求得图中顶点的度(出度和入度)而提出来的。用十字链表来存储有向图,可以达到高效的存取效果。它是综合邻接表和逆邻接表形式的一种链式存储结构。
6.邻接多重表:
- 邻接多重表主要用于存储无向图。如果用邻接表存储无向图,每条边的两个边结点分别在以该边所依附的两个顶点为头结点的链表中,这给图的某些操作带来不便。因此,在进行这一类操作的无向图的问题中采用邻接多重表作存储结构更为适宜。
教材学习中的问题和解决过程
- 问题1:关于图的六种实现,只看懂了邻接列表,邻接矩阵,对于剩下的三种则完全没有理解。
- 问题1解决方案:在询问了同学之后,理解了剩下的三种实现策略,可后面想要编写代码却完全卡死,看书也看不懂,于是去百度了一下,发现了一片博客,里面有详尽的图的各种实现方法。(https://blog.csdn.net/whuhan2013/article/details/51760211)
-
邻接表实现无向图(01) ListUDG是邻接表对应的结构体。
mVexNum是顶点数,mEdgNum是边数;mVexs则是保存顶点信息的一维数组。(02) VNode是邻接表顶点对应的结构体。
data是顶点所包含的数据,而firstEdge是该顶点所包含链表的表头指针。(03) ENode是邻接表顶点所包含的链表的节点对应的结构体。
ivex是该节点所对应的顶点在vexs中的索引,而nextEdge是指向下一个节点的
代码调试中的问题和解决过程
-
问题1:无
码云链接
结对及互评
博客中值得学习的或问题:
- 博客排版工整,界面很美观,并且本周还对博客排版、字体做了调整,很用心
- 问题总结做得很全面:对课本上不懂的代码会做透彻的分析,即便可以直接拿过来用而不用管他的含义
本周结对学习情况
- 20172315
- 20172318
结对学习内容
- 边集数组,十字链表实现图