动态规划——线性DP.1

动态规划算法通常用于求解具有某种最优性质的问题。

那它和贪心有区别吗？

当然有。不然叫动态规划干啥？

幼儿园英语老师：DP是啥？

小盆友：Dog&Peppa pig

英语老斯：恩恩！真聪明！

然而，你是小盆友吗？

如果是

 

如果不是，

 

DP是D****** P*******的缩写。

意思是动态规划。

聪明的bolt告诉你：是Dynamic Programming的缩写！！！

 

动态规划注重     表示状态，转移状态

 so

讲一个栗子：

LIS：

最长上升子序列

 

这是线性动态规划中最经典的栗子之一。

最长上升子序列（Longest Increasing Subsequence，LIS），指一个序列中最长的单调递增的子序列。

注意不是子串，所以可以不相邻。

比如说：

序列：3   2   1   4   6   8   7   9

它的LIS是5

3   4   6   8   9

或3   4   6   7   9

或2   4   6   8   9

······

还有很多种情况。

于是我们珂以得出：

动态规划的最优解，有不同的组合情况，但答案只有一个。

所以，如果NOIP出了动态规划的题目时，一般会叫你求值，而不是求情况。

 

这是好处！

BUT，有的老师不会好心，会给更多限制条件，使Ans只有一种情况，那就更有难度了。

 

LIS问题要用动态规划做。

方法一：

这是一个好理解的方法。

但是更好使耗时

 

 

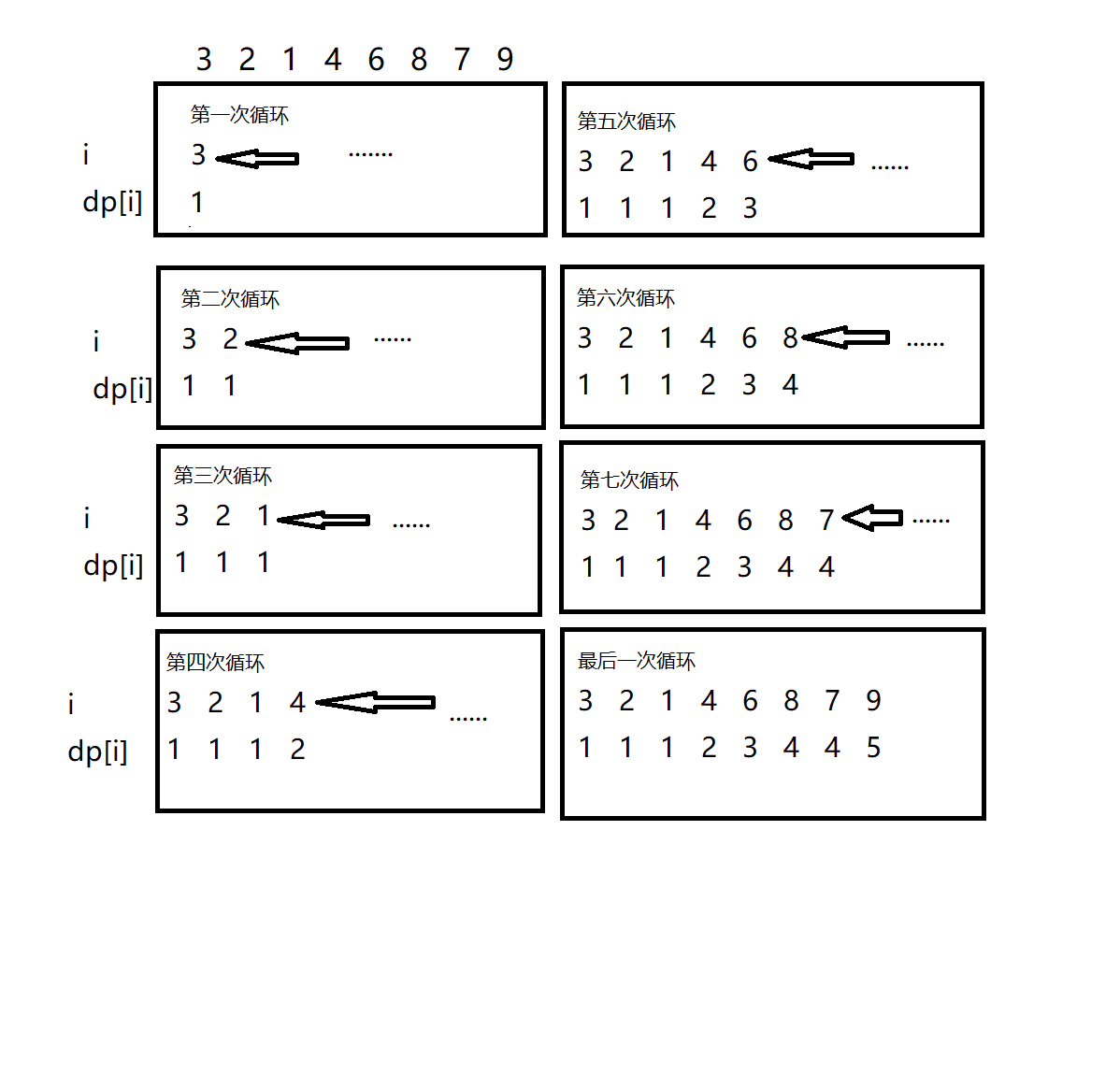
不难看出，dp [ i ]就是第 i 个数的LIS

那代码怎么实现的呢？

先别急，我们在举个生活中的栗子。

 

老师要你算1+2+3+4+5+6+7+8+9=？时，你会算得45，

老师再问你1+2+3+4+5+6+7+8+9+10=？时，你是会用1+···+10，还是用之前算的45+10？

聪明人会用后面一种。

 

所以，我们根据这个方便的原理，发现我每次计算dp [ i ] 时，如果用到了前面的 dp 值，则会减少一定的计算量。

 

在我们每次枚举一个数的dp值时，只要扫描在它前面比它小的数，那些比他小的数的dp值的最大值+1就是所求数的dp值

因为比所求数小的数的dp值表示它的LIS，再来一个比它大的数，大树数的LIS就等于小数的LIS+1.

但由于小数的LIS有大有小，我们又要求最长子序列，我们就要取最大值。

 

一番思考后，我们找到了状态转移方程，也就是动态规划中最重要的东西：

对于每一个 i ，我们枚举它前面的数 j，if (i > 它前面的数 j )   dp [ i ] = max ( dp [ i ] , dp [ j ] + 1 ) ;

 

这个算法的时间复杂度是O(n^2)的，慎用。

 

code:

int n,a[1001]/*用来存序列*/,dp[1001]/*dp值*/;//数组大小根据题目而定。
cin>>n;
dp[1]=1;                                   //1的dp值为1
for(int i=1;i<=n;i++)
    cin>>a[i];
for(int i=1;i<=n;i++)
{
    for(int j=1;j<i;j++)
    {
        if(a[i]>a[j])
        {
            dp[i]=max(dp[i],dp[j]+1);      //状态转移
        }
    }
}
cout<<dp[n]<<endl;

 注意要初始化dp [ 1 ] = 1.剩下的为 0.

还有另一种时间复杂度为 n log n 的LIS算法

 

看，栗子！

2   1   5   3   6   4   6   3 

在 dp 值相同的情况下，保留较小的数显然更好。因为后面的数若能跟较大的数构成上升子序列，也一定能能较小的数构成上升子序列，反之则不一定。例如 a_3=5 与 a_4=3 的 dp 均为 2，但 a_6=4 不能与 a_3=5 构成上升子序列，而可以和 a_4=3 构成上升子序列。 因此，不同的 dp 值只需要存一个对应的最小值，将这个最小值顺序排列，他们一定是升序（严格来说是不下降）的。 于是，借助二分查找的方式，就可以很快查到更新的值，整体时间复杂度 O(nlogn)。

这个就是上面的一个优化，也没有太多可讲的，自己打一遍代码也就熟了。

code：

const int maxn=1e5+5;
int a[maxn];
int n;
int dp[maxn];
int ans=1;
int find(int x){
    int l=1,r=ans,m;
    while(l<r){
        m=l+(r-l)/2;
        if(dp[m]>=a[x]){
            r=m;
        } 
        else{
            l=m+1;
        }
    }
    return l;
}//二分查找 
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    dp[1]=a[1];
    for(int i=2;i<=n;i++){
        if(a[i]>dp[ans]){
            dp[++ans]=a[i];
        }
        else{
            int pos=find(i);
            dp[pos]=a[i];
        }
    }
    printf("%d",ans);
    return 0;
}

这就是LIS问题，希望大家好好理解这个问题，因为他真的狠重要！

 

今天的分享就到这里，我们下次见。