LeetCode 684. Redundant Connection 冗余连接(C++/Java)

题目：

In this problem, a tree is an undirected graph that is connected and has no cycles.

The given input is a graph that started as a tree with N nodes (with distinct values 1, 2, ..., N), with one additional edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed.

The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [u, v] with u < v, that represents an undirected edge connecting nodes u and v.

Return an edge that can be removed so that the resulting graph is a tree of N nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array. The answer edge [u, v] should be in the same format, with u < v.

Example 1:

Input: [[1,2], [1,3], [2,3]]
Output: [2,3]
Explanation: The given undirected graph will be like this:
  1
 / \
2 - 3

 

Example 2:

Input: [[1,2], [2,3], [3,4], [1,4], [1,5]]
Output: [1,4]
Explanation: The given undirected graph will be like this:
5 - 1 - 2
    |   |
    4 - 3

分析：

给定一个边的序列来构建一个无向图，求出序列中第一条使得无向图成为有环无向图的边。

可以利用dfs来进行搜索，每新加入一条边，查看原来的无向图中是否存在这条边两个顶点间连通分量，如果有的话就会构成环。

dfs的时间复杂度为O(n^2)，我们可以利用并查集的思想解决这道题。

以[1,2], [1,3], [2,3]为例。

我们新开辟一个数组用来保存节点间的关系，新加入边[1,2]时。

如果parents数组为0，则将对应索引的值初始化为自身，也就代表两个结点指向的是自己，利用并查集的思想，连通的节点之间所属同一集合。对两个结点进行查询，返回他们最终的父结点，如果两个结点最终的父结点相同，代表他们在同一个集合中，无向图加入这条边就有环了，如果没有的话，将这两个集合合并。

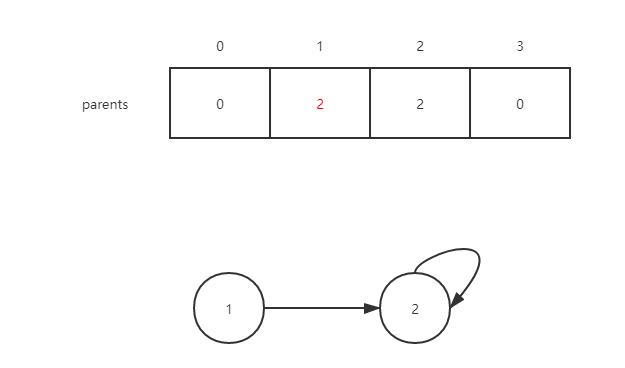
然后加入边[1,3],结果如下图

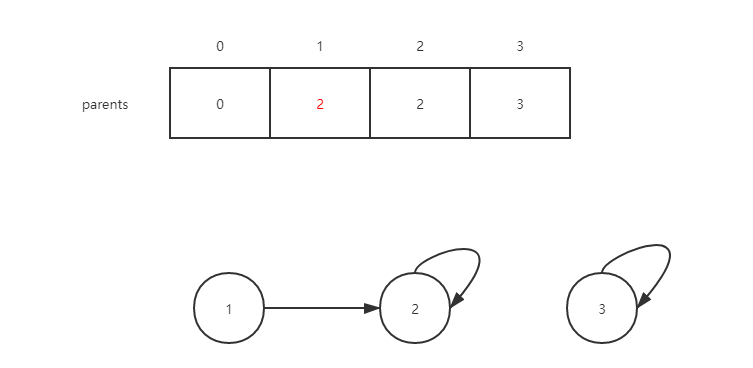
查找1和3的父结点，分别返回2，和3，他们不相同，将两个集合合并，也就是将2的父亲标记为3

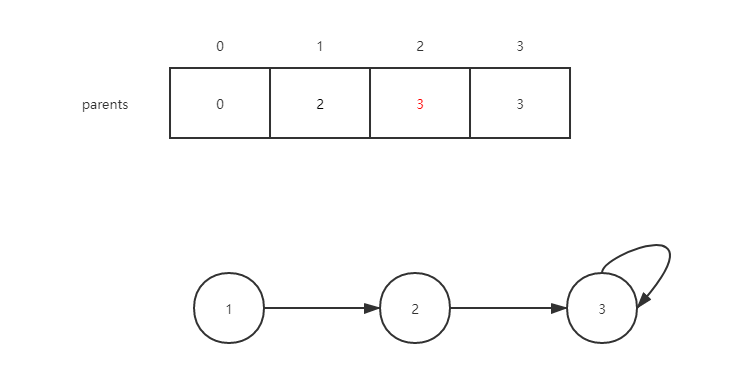
最后加入边[2,3]，我们通过上面的图可以发现2,3的父结点最终都是3，是相同的，证明他们在同一集合中，直接返回这条边即可。

在这里并查集可以进行一定的优化，例如合并时，可以将容量小的集合合并到大的集合中，这样修改结点关系的操作较小，而且每次搜索最终父结点时，可以在查询父结点时，同时修改其父结点的关系，减少下次查询消耗的时间。

程序：

C++

class Solution {
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        vector<int> parents(edges.size()+1, 0);
        for(auto edge:edges){
            int u = edge[0];
            int v = edge[1];
            if(!parents[u])
                parents[u] = u;
            if(!parents[v])
                parents[v] = v;  
            int pu = find(u, parents);
            int pv = find(v, parents);
            if(pu == pv)
                return edge;
            parents[pu] = pv;
        }
        return {};
    }
private:
    int find(int node, vector<int> &parents){
        while(node != parents[node]){
            parents[node] = parents[parents[node]];
            node = parents[node];
        }
        return node;
    }
};

Java

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int[] parents = new int[edges.length+1];
        for(int[] edge:edges){
            int u = edge[0];
            int v = edge[1];
            if(parents[u] == 0)
                parents[u] = u;
            if(parents[v] == 0)
                parents[v] = v;
            int pu = find(u, parents);
            int pv = find(v, parents);
            if(pu == pv)
                return edge;
            parents[pu] = pv;
        }
        return null;
    }
    private int find(int node, int[] parents){
        while(node != parents[node]){
            parents[node] = parents[parents[node]];
            node = parents[node];
        }
        return node;
    }
}