野路子码农系列(8)我终于大致搞懂了GBDT
由于下下周要在组里介绍一个算法,最近开始提前准备,当初非常自信地写下自己最喜欢的GBDT,但随着逐步深入,发现其实自己对这个算法的细节并不是非常了解,了解的只是一些面试题的答案而已……(既然没有深入了解,又怎么配说最喜欢呢?)
此外,由于野路子的鄙人数学功底不行,对公式的理解非常捉急,故而在本次探究和摸索的过程当中,参考了不少GBDT相关的博客。然而我发现有些博客对细节(尤其是分类)语焉不详,有些则是写着写着混到Xgboost去了,总之似乎并没有能找到一篇足够“通俗易懂”的。于是我便想把一个完整的,通俗的例子记录下来,帮助后来人理解GBDT。以下包括二分类和回归的实例各一个,逐步推导(某些公式或者结论我实在没实力推导,就略过一下)。
1、先说一些基础的东西
GBDT模型训练的步骤:
- 初始化根节点 F0(x),如果是分类模型,计算其对应的概率p0;
- 计算“伪残差”,回归模型即为 y - F(x),而分类模型为 y - p,这个伪残差即为我们接下来要拟合或者说逼近的目标;
- 遍历各个特征和其分裂阈值,找出最优的特征和分裂阈值;
- 按照该阈值分裂该特征后,分别计算左右叶节点的对应值 f(x);
- 通过学习率 lr 和 Fm(x) = Fm-1(x) + lr × fm(x) 计算下一个 F(x),如果是分类模型,计算其对应的概率p;
- 重复第(2) ~ (5)步。
以上内容当然不够详实,我们通过实例就明白了。
2、二分类实例
我们就用网上的一个实例吧:

单一特征x,y为目标值,非常简单的二分类。假设我们的树深度均为1,损失函数为log loss。
(1)我们首先按照第1步,计算 F0(x),分类的 F0(x) 比较特殊,为 ln(pos/neg),即logit。在这里也就是 ln(4/6) = -0.4055 (4个1,6个0),所有x对应的 F0(x) 全都一样。
由于这是分类问题,我们将 F0(x) 转化为概率 p0,这一步通过一个简单的Logistic函数实现,即 1/(1+e-F(x)) ,此处我们得到一堆0.4(因为 F0(x) 都一样)。
(2)接下来进入第2步,计算伪残差(姑且叫这个名字,因为像残差但不是真正的残差),这个也很简单,用 y 减去我们刚刚算出来的一堆0.4就行,我们得到:
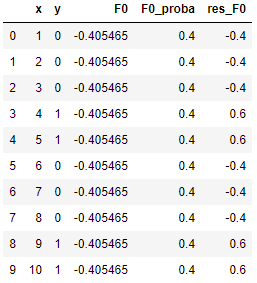
重复一遍,这个伪残差即为我们接下来要拟合或者说逼近的目标。
(3)然后是第3步,寻找分裂点,由于这里我们只有一个特征 x,所以我们只需要搜索 x 的所有分裂点(阈值)即可。我们需要搜索一个能让分裂准则(criterion)达到最小的分裂点。
这里需要说明的是,GBDT的criterion不是gini!!!千万不要跟CART搞混了。通常我们采用friedman_mse,网上许多例子对于这个mse的计算都着墨颇少,我琢磨了很久可算是琢磨出来了(智商捉急)。
首先我们针对特征 x 枚举每个分裂点(0.5,1.5,2.5,...,10.5),每个分裂点你可以得到左侧子树和右侧子树,比如分裂点为8.5,左侧子树为 x ≤ 8.5 (即 x = 1, 2, 3, 4, 5, 6, 7, 8),右侧子树为 x>8.5(即 x = 9, 10)。
然后我们计算各个分裂点下,左侧子树和右侧子树各自伪残差的均值。比如分裂点为8.5时,左侧伪残差的均值为 (-0.4 - 0.4 -0.4 + 0.6 + 0.6 - 0.4 - 0.4 - 0.4) / 8 = -0.15,右侧均值为 (0.6 + 0.6) / 2 = 0.6。
接着我们用左右侧的每个伪残差减去其对应的均值,得到误差error,再计算其对应的平方误差square_error,这个值描述了我们离我们要逼近的目标(伪残差)还差多少:
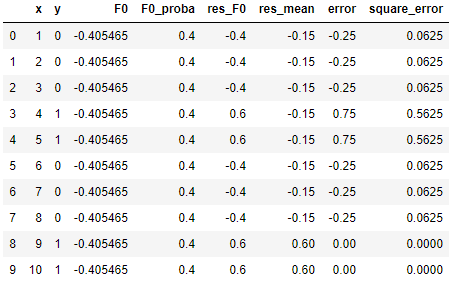
我们将所有 x 对应的square_error加和起来,得到 ∑square_error = 1.5。我们对 x 的每个分裂点(0.5,1.5,2.5,...,10.5)都这么计算一遍,最后得出 ∑square_error 的最小值为1.5,此时的分裂点为 x = 8.5。
(4)分裂完成后,就需要计算左右子树的值。具体计算方法与损失函数的选取有关,推导详见Friedman的论文,此处不做展开(数学白痴),仅说结论:
二分类问题常用的损失函数log loss对应的子树值计算方法为:
![]()
假设我们计算的是左侧子树,首先看一下分子,分子很简单,即左侧伪残差的和,即 (-0.4 - 0.4 -0.4 + 0.6 + 0.6 - 0.4 - 0.4 - 0.4) = -1.2。
我们再看分母,分母是 (y - 伪残差) × (1 - y + 伪残差) 的和,比如 x = 1时,其为 [0 - (-0.4)] × [1 - 0 + (-0.4)] = 0.24,以此类推,我们可以算出左侧所有情况下的分母,其总和为1.92。
因此左侧子树的值也就是 -1.2 / 1.92 = -0.625,我们可以用同样的方法算出右侧子树的值,为2.5。这两个就是第1棵树的 f(x)。
至此,第1颗树的结构完全确定下来了,即为:

(5)现在我们需要更新 F(x) 了。根据GBDT的加法原则,我们只需要将上一棵树的 F(x) 加上学习率乘以本棵树的 f(x)。即 Fm(x) = Fm-1(x) + lr × fm(x),此处也就是 F1(x) = F0(x) + lr × f1(x)。
此处 F0(x) 即我们之前算出的 ln(4/6) = -0.4055 ,f1(x) 即我们刚才计算的左右子树的值 -0.625 和 2.5。每一次更新的步长可以通过line search得到,但比较麻烦,通常取而代之都是采用一个固定的学习率(sklearn中也是这样做的)。
例如 x = 1时,该节点分在左侧,所以f1(1) = -0.625,因此 F1(1) = -0.4055 + 0.1 × (-0.625) = -0.468;类似的, x = 9时,该节点分在右侧,所以f1(1) = 2.5,因此 F1(1) = -0.4055 + 0.1 × 2.5 = -0.1555。据此,我们可以算出每个x对应的F1(x),如下表:
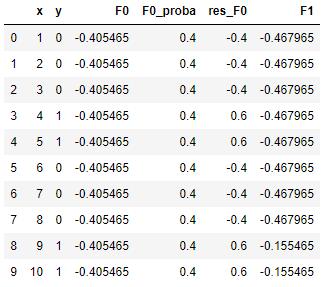
当然,为了得到概率,我们还得Logistic一下,通过 1/(1+e-F1(x)) ,我们得到更新后的概率 p1:
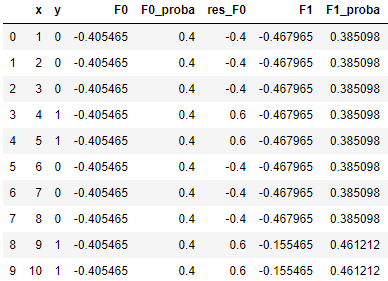
(6)假如我们要再加2棵树,我们可以循环利用(2)~(5)的方法,我们计算新的伪残差 res_F1,以此算出第2棵树的最佳分裂点(仍然是 x = 8.5),计算左右子树的值(左:-0.5705,右:2.168),乘以学习率0.1后拼接到 F1(x) 上,从而得到 F2(x);以此类推,第3棵树的最佳分裂点为 x = 3.5,左右子树的值为,左:-1.5915,右:0.6663,类似的方法可以得到F3(x),最终转化成概率。
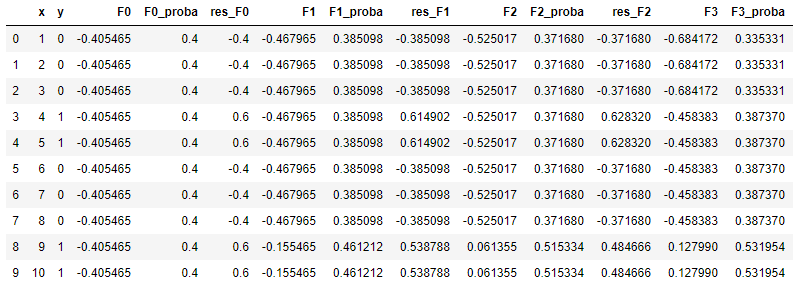


我们可以用来sklearn中的GradientBoostingClassifier来核对一下结果,应当是完全一致的(除了精度差异)。
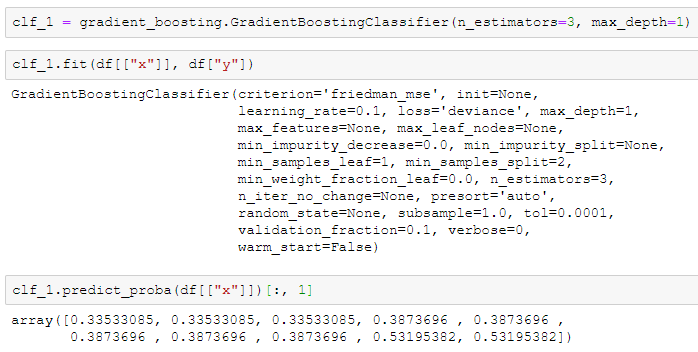
3、回归实例
GBDT的回归比分类更为简单,我们省去了计算概率这一步,而且节点值的计算也相对容易一些。 同样,我们用网上的实例:

同样简单起见,树深度均为1,损失函数为MSE。
(1)第1步初始化,计算 F0(x),回归的 F0(x) 非常简单,取平均就行,也就是 y 的平均值7.307。
(2)第2步,计算伪残差,也很简单,y - F0(x),如下表:
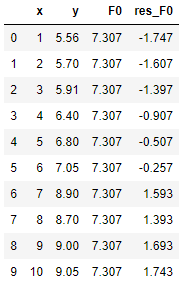
(3)第3步,寻找分裂点,由于这里我们只有一个特征 x,所以我们只需要搜索 x 的所有分裂点(阈值)即可。非常幸运的是,回归问题的分裂准则通常依然采用的是friedman_mse,所以这个过程和我们在分类中的一模一样。
我们同样枚举分裂点,分别计算左右侧伪残差的均值,计算伪残差与各自均值的平方误差,寻找使 ∑square_error 最小的分裂阈值。
此处,我们通过枚举计算可以得到,当 x = 6.5 时,∑square_error 最小,为1.9300。
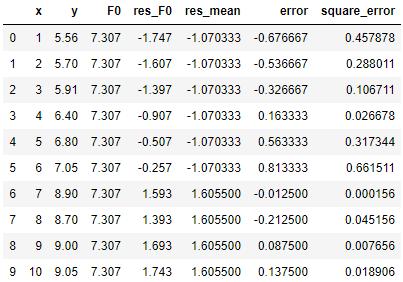
(4)得到分裂点之后,我们需要计算左右子树的值。之前说过,具体计算方法与损失函数的选取有关,通常回归问题的损失函数我们会选择MSE。MSE对应的计算方法非常简单——取平均……
我们按照 x = 6.5 分裂左右子树后,左侧为 x = 1, 2, 3, 4, 5, 6,其伪残差的均值为 (-1.747 - 1.607 - 1.397 - 0.907 - 0.507 -0.257) / 6 = -1.0703;类似的,右侧为 x = 7, 8, 9, 10,其伪残差的均值为 (1.593 + 1.393 + 1.693 + 1.743) / 4 = 1.6055。此二者即左右子树的值。
至此,我们也就得到了第1棵树的结构:

(5)类似的,我们来更新 F(x) 。根据GBDT的加法原则,公式是一模一样的,即 Fm(x) = Fm-1(x) + lr × fm(x),此处也就是 F1(x) = F0(x) + lr × f1(x)。同样,我们假设学习率设置为0.1,我们通过跟分类一样的办法计算得到 F1(x):
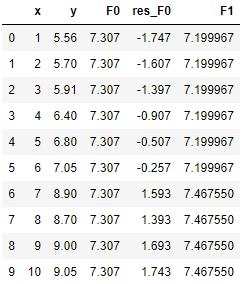
如前所述,回归不需要转化成概率,F1(x) 所见即所得。
(6)同样地,假如我们要再加2棵树,我们可以循环利用(2)~(5)的方法,算伪残差,找分裂点,算左右子树的值,更新F(x) 。本例中3棵树的最佳分裂点都在 x = 6.5。
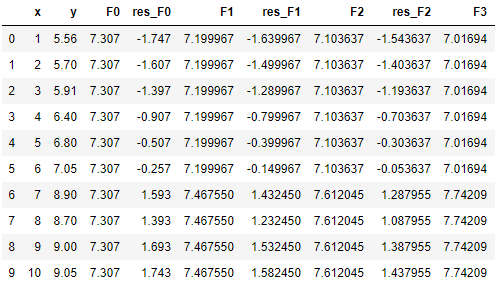


我们同样可以用来sklearn中的GradientBoostingRegressor来核对一下结果,应当是完全一致的(除了精度差异)。
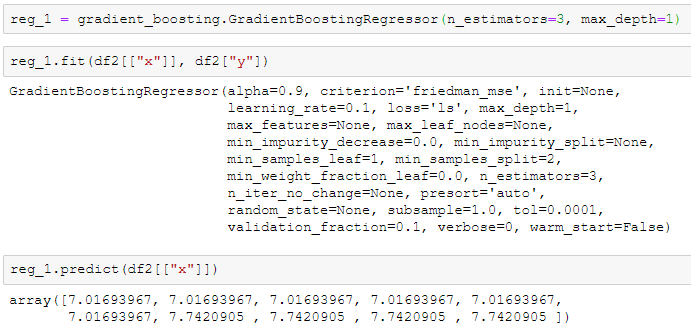
4、更进一步
至此,我终于可以大言不惭地说我大致搞懂了GBDT了。当然由于我举的例子都非常的简单,在于实际对接的过程中我们可能还会有一些问题,比如:
(1)例子里的树深度都是1,如果深度更深该怎么办?
深度更深时其实基本步骤还是一样的,但在第3步,寻找最佳分裂点时,我们可能要多做几步。首先我们按照同样的方法先找到最佳分裂点分裂1次(depth= 1),然后在分裂完的基础上对左右子树再次进行分裂,寻找最佳分裂点的准则和方法依然沿用。
比如刚才的分类问题,我们第1棵树分裂完一次之后,左侧为 x = 1, 2, 3, 4, 5, 6, 7, 8,右侧为 x = 9, 10。假如我们的树深度设置为2,那么我们需要再进行一次分裂。由于右侧已经纯净(y都为1),所以无须分裂,我们对左侧再次枚举每个分裂点,得到下一级的左右子树(depth = 2),对子树计算伪残差与其均值的平方误差,找到 ∑square_error 的分裂点。所有操作都是如出一辙的重复而已。
类似的,计算各个子树的值也是套用同样的方法,只不过要多算即可子树而已。最后乘上学习率,再加到上一级函数 F(x) 上即可。
(2)例子里只有1个特征,如果我有几个特征怎么办?
方法没有任何变化,但在第3步,寻找最佳分裂点时,我们需要枚举每个特征的每个分裂点来进行计算,最后选取最优的分裂特征上的最佳分裂点,仅此而已。
希望本期的内容也足够通俗易懂。回想前几天推不出分类时晚上做梦都在想,今天终于可以浑身舒畅了!
配套Notebook:
https://github.com/SilenceGTX/algorithms/blob/master/GBDT.ipynb



