(六)OpenCV-Python学习—边缘检测2

　　在上一节中都是采用一阶差分(导数)，进行的边缘提取。也可以采用二阶差分进行边缘提取，如Laplacian算子，高斯拉普拉斯(LoG)边缘检测，高斯差分(DoG)边缘检测，Marr-Hidreth边缘检测。这些边缘提取算法详细介绍如下：

1. Laplacian算子

　　Laplacian算子采用二阶导数，其计算公式如下：(分别对x方向和y方向求二阶导数，并求和)

　　其对应的Laplacian算子如下：

　　其推导过程如下：

　　opencv中提供Laplacian()函数计算拉普拉斯运算，其对应参数如下：

dst = cv2.Laplacian(src, ddepth, ksize, scale, delta, borderType)
    src: 输入图像对象矩阵,单通道或多通道
    ddepth:输出图片的数据深度,注意此处最好设置为cv.CV_32F或cv.CV_64F
    ksize: Laplacian核的尺寸，默认为1，采用上面3*3的卷积核
    scale: 放大比例系数
    delta: 平移系数
    borderType: 边界填充类型

　　下面为使用代码及其对应效果：

#coding:utf-8

import cv2
img_path= r"C:\Users\silence_cho\Desktop\Messi.jpg"
img = cv2.imread(img_path)
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

dst_img = cv2.Laplacian(img, cv2.CV_32F)
laplacian_edge = cv2.convertScaleAbs(dst_img)  #取绝对值后，进行归一化

dst_img_gray = cv2.Laplacian(img_gray, cv2.CV_32F)
laplacian_edge_gray = cv2.convertScaleAbs(dst_img_gray)  #取绝对值后，进行归一化

cv2.imshow("img", img)
cv2.imshow("laplacian_edge", laplacian_edge)
cv2.imshow("img_gray", img_gray)
cv2.imshow("laplacian_edge_gray ", laplacian_edge_gray)
cv2.waitKey(0)
cv2.destroyAllWindows()

cv2.Laplacian()

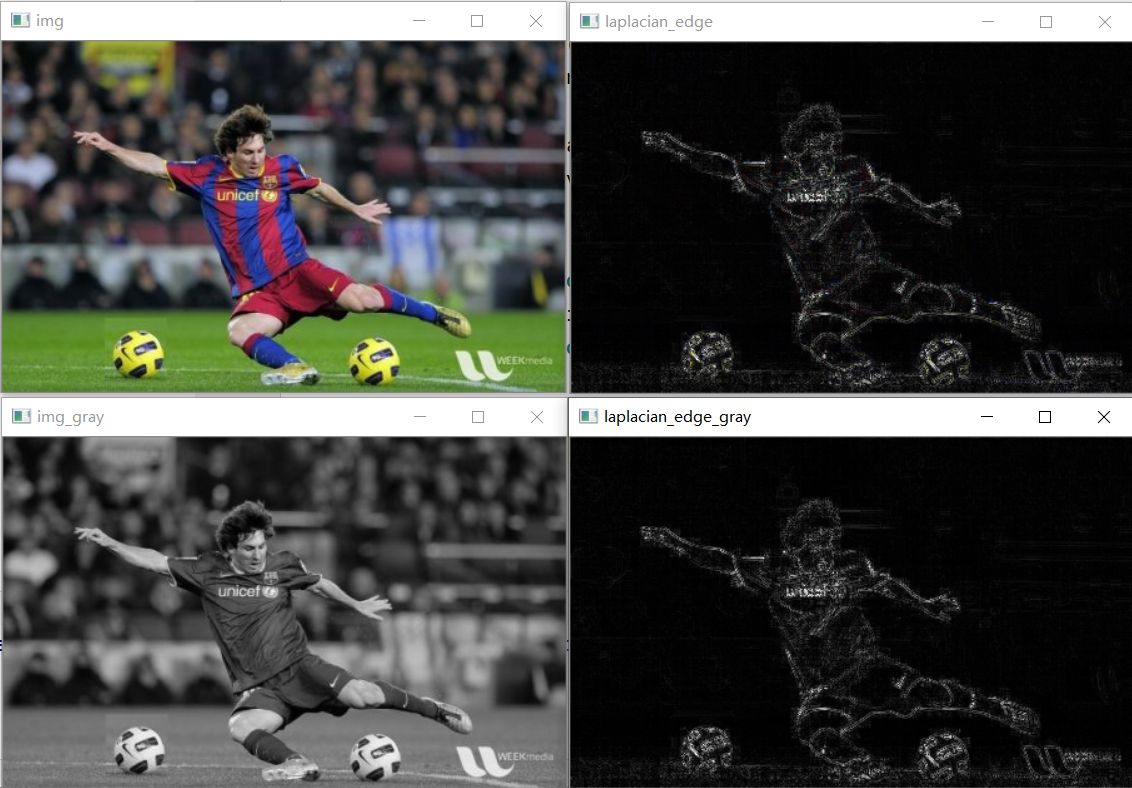
　　Laplacina算子进行边缘提取后，可以采用不同的后处理方法，其代码和对应效果如下：

#coding:utf-8
import cv2
import numpy as np

img_path= r"C:\Users\silence_cho\Desktop\Messi.jpg"
img = cv2.imread(img_path)
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
dst_img_gray = cv2.Laplacian(img_gray, cv2.CV_32F)

# 处理方式1
laplacian_edge = cv2.convertScaleAbs(dst_img_gray)  #取绝对值后，进行归一化
# convertScaleAbs等同于下面几句：
# laplacian_edge = np.abs(laplacian_edge)
# laplacian_edge = laplacian_edge/np.max(laplacian_edge)
# laplacian_edge = laplacian_edge*255  #进行归一化处理
# laplacian_edge = laplacian_edge.astype(np.uint8)

# 处理方式2
laplacian_edge2 = np.copy(laplacian_edge)
# laplacian_edge2[laplacian_edge > 0] = 255
laplacian_edge2[laplacian_edge > 255] = 255
laplacian_edge2[laplacian_edge <= 0] = 0
laplacian_edge2 = laplacian_edge2.astype(np.uint8)


#先进行平滑处理
gaussian_img_gray = cv2.GaussianBlur(dst_img_gray, (3, 3), 1)
laplacian_edge3 = cv2.convertScaleAbs(gaussian_img_gray)  #取绝对值后，进行归一化

cv2.imshow("img_gray", img_gray)
cv2.imshow("laplacian_edge", laplacian_edge)
cv2.imshow("laplacian_edge2", laplacian_edge2)
cv2.imshow("laplacian_edge3", laplacian_edge3)
cv2.waitKey(0)
cv2.destroyAllWindows()

Laplacian进行不同后处理

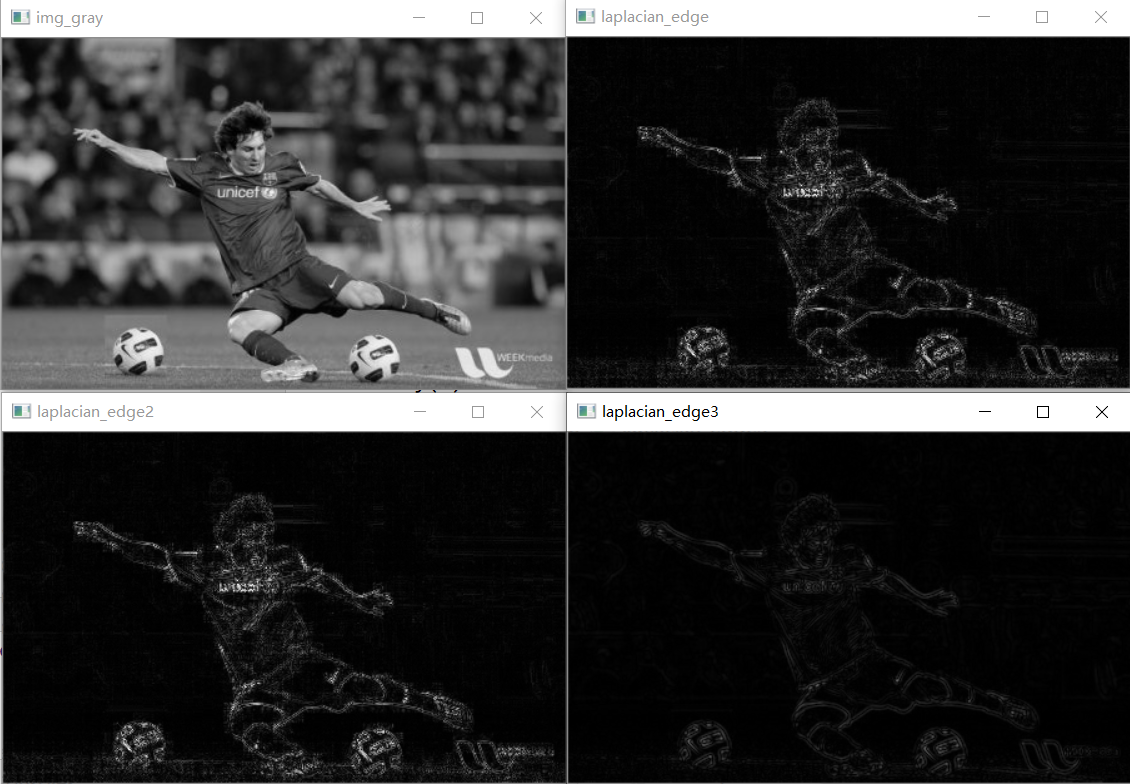
2. 高斯拉普拉斯(LoG)边缘检测

　　拉普拉斯算子没有对图像做平滑处理，会对噪声产生明显的响应，所以一般先对图片进行高斯平滑处理，再采用拉普拉斯算子进行处理，但这样要进行两次卷积处理。高斯拉普拉斯(LoG)边缘检测，是将两者结合成一个卷积核，只进行一次卷积运算。

高斯拉普拉斯(LoG)，指的是二维高斯函数的拉普拉斯变换，其推导公式如下：

　　下面为一个标准差为1，3*3的LoG卷积核示例：

　　用python实现高斯拉普拉斯LoG，代码及其对应效果如下：

#coding:utf-8
import numpy as np
from scipy import signal
import cv2


def createLoGKernel(sigma, size):
    H, W = size
    r, c = np.mgrid[0:H:1.0, 0:W:1.0]
    r -= (H-1)/2
    c -= (W-1)/2
    sigma2 = np.power(sigma, 2.0)
    norm2 = np.power(r, 2.0) + np.power(c, 2.0)
    LoGKernel = (norm2/sigma2 -2)*np.exp(-norm2/(2*sigma2))  # 省略掉了常数系数 1\2πσ4

    print(LoGKernel)
    return LoGKernel

def LoG(image, sigma, size, _boundary='symm'):
    LoGKernel = createLoGKernel(sigma, size)
    edge = signal.convolve2d(image, LoGKernel, 'same', boundary=_boundary)
    return edge


if __name__ == "__main__":
    img_path= r"C:\Users\silence_cho\Desktop\Messi.jpg"
    img = cv2.imread(img_path, 0)
    LoG_edge = LoG(img, 1, (11, 11))
    LoG_edge[LoG_edge>255] = 255
    # LoG_edge[LoG_edge>255] = 0
    LoG_edge[LoG_edge<0] = 0
    LoG_edge = LoG_edge.astype(np.uint8)

    LoG_edge1 = LoG(img, 1, (37, 37))
    LoG_edge1[LoG_edge1 > 255] = 255
    LoG_edge1[LoG_edge1 < 0] = 0
    LoG_edge1 = LoG_edge1.astype(np.uint8)

    LoG_edge2 = LoG(img, 2, (11, 11))
    LoG_edge2[LoG_edge2 > 255] = 255
    LoG_edge2[LoG_edge2 < 0] = 0
    LoG_edge2 = LoG_edge2.astype(np.uint8)

    cv2.imshow("img", img)
    cv2.imshow("LoG_edge", LoG_edge)
    cv2.imshow("LoG_edge1", LoG_edge1)
    cv2.imshow("LoG_edge2", LoG_edge2)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

高斯拉普拉斯LoG边缘检测

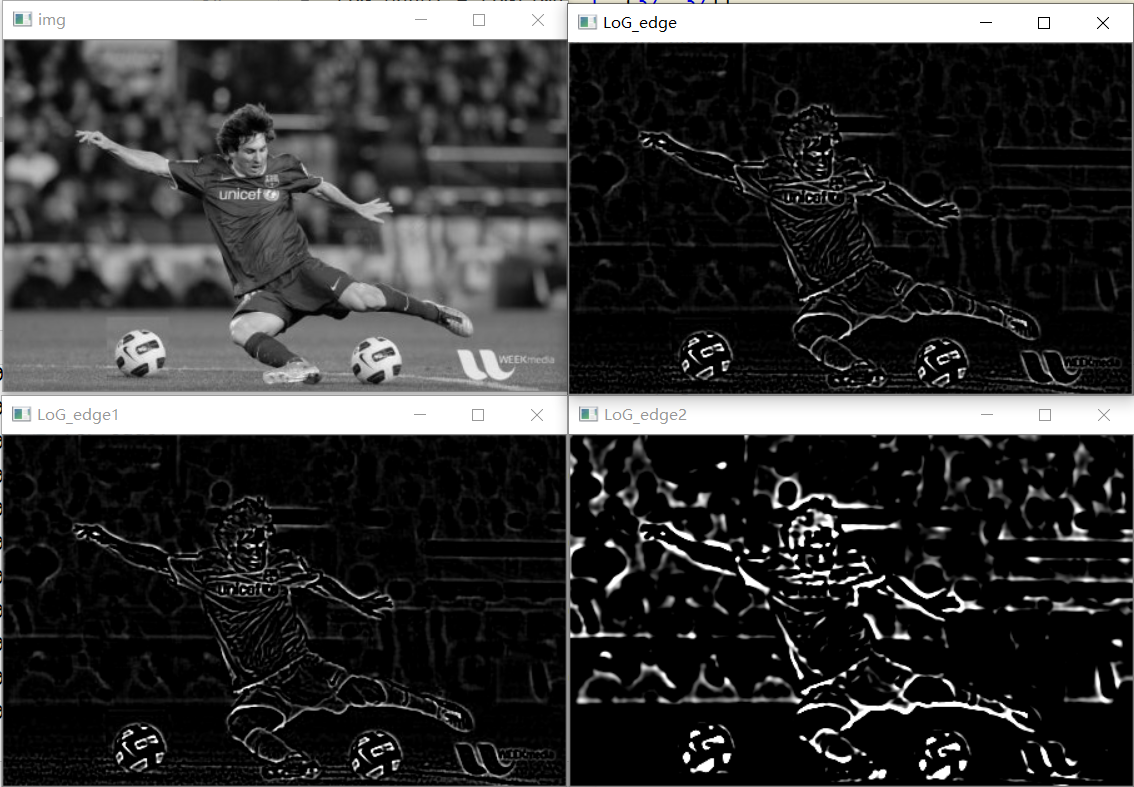
3. 高斯差分(DoG)边缘检测

　　高斯差分(Difference of Gaussian, DoG), 是高斯拉普拉斯(LoG)的一种近似，两者之间的关系推导如下：

　　高斯差分(Difference of Gaussian, DoG)边缘检测算法的步骤如下：

构建窗口大小为HxW，标准差为 $的DoG卷积核(H, W一般为奇数，且相等)$
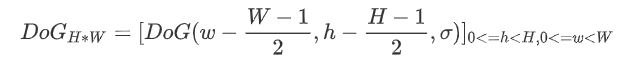
图像与两个高斯核卷积，卷积结果计算差分
边缘后处理

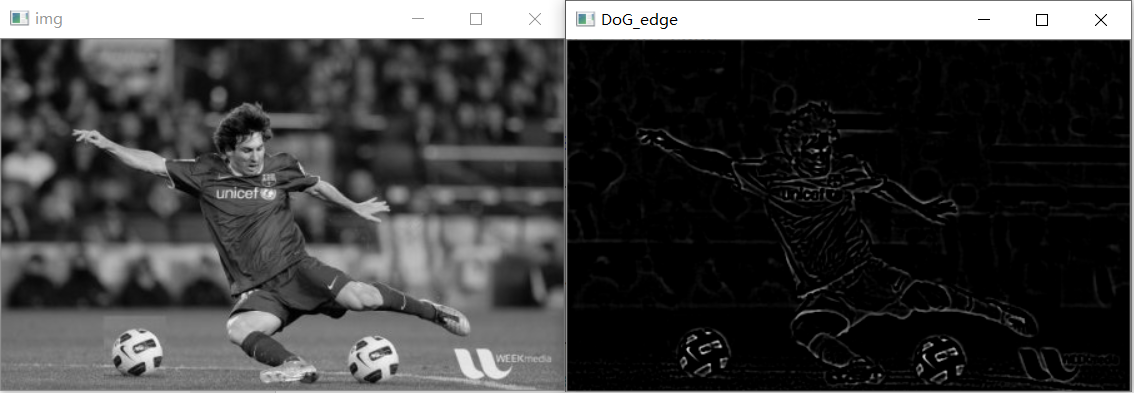
　　python代码实现DoG边缘提取算法，代码和结果如下：

#coding:utf-8

import cv2
import numpy as np
from scipy import signal

# 二维高斯卷积核拆分为水平核垂直一维卷积核，分别进行卷积
def gaussConv(image, size, sigma):
    H, W = size
    # 先水平一维高斯核卷积
    xr, xc = np.mgrid[0:1, 0:W]
    xc = xc.astype(np.float32)
    xc -= (W-1.0)/2.0
    xk = np.exp(-np.power(xc, 2.0)/(2*sigma*sigma))
    image_xk = signal.convolve2d(image, xk, 'same', 'symm')

    # 垂直一维高斯核卷积
    yr, yc = np.mgrid[0:H, 0:1]
    yr = yr.astype(np.float32)
    yr -= (H-1.0)/2.0
    yk = np.exp(-np.power(yr, 2.0)/(2*sigma*sigma))
    image_yk = signal.convolve2d(image_xk, yk, 'same','symm')
    image_conv = image_yk/(2*np.pi*np.power(sigma, 2.0))

    return image_conv

#直接采用二维高斯卷积核，进行卷积
def gaussConv2(image, size, sigma):
    H, W = size
    r, c = np.mgrid[0:H:1.0, 0:W:1.0]
    c -= (W - 1.0) / 2.0
    r -= (H - 1.0) / 2.0
    sigma2 = np.power(sigma, 2.0)
    norm2 = np.power(r, 2.0) + np.power(c, 2.0)
    LoGKernel = (1 / (2*np.pi*sigma2)) * np.exp(-norm2 / (2 * sigma2))
    image_conv = signal.convolve2d(image, LoGKernel, 'same','symm')

    return image_conv

def DoG(image, size, sigma, k=1.1):
    Is = gaussConv(image, size, sigma)
    Isk = gaussConv(image, size, sigma*k)

    # Is = gaussConv2(image, size, sigma)
    # Isk = gaussConv2(image, size, sigma * k)

    doG = Isk - Is
    doG /= (np.power(sigma, 2.0)*(k-1))
    return doG

if __name__ == "__main__":
    img_path= r"C:\Users\silence_cho\Desktop\Messi.jpg"
    img = cv2.imread(img_path, 0)
    sigma = 1
    k = 1.1
    size = (7, 7)
    DoG_edge = DoG(img, size, sigma, k)
    DoG_edge[DoG_edge>255] = 255
    DoG_edge[DoG_edge<0] = 0
    DoG_edge = DoG_edge / np.max(DoG_edge)
    DoG_edge = DoG_edge * 255
    DoG_edge = DoG_edge.astype(np.uint8)

    cv2.imshow("img", img)
    cv2.imshow("DoG_edge", DoG_edge)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

高斯差分(DoG)边缘检测算法

4. Marri-Hildreth边缘检测算法

　　高斯拉普拉斯和高斯差分边缘检测，得到边缘后，只进行了简单的阈值处理，Marr-Hildreth则对其边缘进行了进一步的细化，使边缘更加精确细致，就像Canny对sobel算子的边缘细化一样。

Marr-Hildreth边缘检测可以细分为三步：

构建窗口大小为H*W的高斯拉普拉斯卷积核(LoG)或高斯差分卷积核(DoG)
图形矩阵与LoG核或DoG核卷积
在第二步得到的结果中，寻找过零点的位置，过零点的位置即为边缘位置

　　第三步可以这么理解，LoG核或DoG核卷积后表示的是二阶导数，二阶导数为0表示的是一阶导数的极值，而一阶导数为极值表示的是变化最剧烈的地方，因此对应到图像边缘提取中，二阶导数为0，表示该位置像素点变化最明显，即最有可能是边缘交接位置。

　　对于连续函数g(x), 如果g(x1)*g(x2) < 0，即 g(x1) 和g(x2) 异号，那么在x1，x2之间一定存在x 使得g(x)=0，则x为g(x)的过零点。在图像中，Marr-Hildreth将像素点分为下面四种情况，分别判断其领域点之间是否异号：

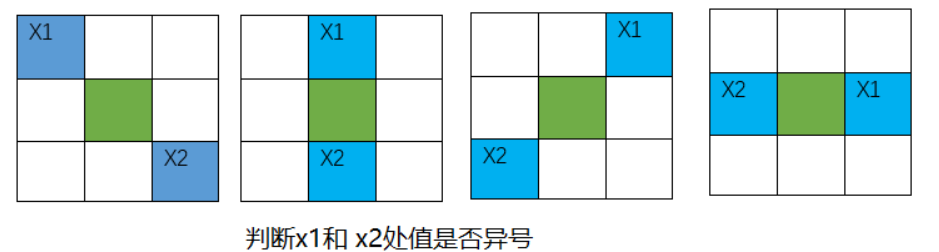
　　 python代码实现Marri-Hildreth边缘检测算法，代码和结果如下所示：

#coding:utf-8

import cv2
import numpy as np
from scipy import signal

# 二维高斯卷积核拆分为水平核垂直一维卷积核，分别进行卷积
def gaussConv(image, size, sigma):
    H, W = size
    # 先水平一维高斯核卷积
    xr, xc = np.mgrid[0:1, 0:W]
    xc = xc.astype(np.float32)
    xc -= (W-1.0)/2.0
    xk = np.exp(-np.power(xc, 2.0)/(2*sigma*sigma))
    image_xk = signal.convolve2d(image, xk, 'same', 'symm')

    # 垂直一维高斯核卷积
    yr, yc = np.mgrid[0:H, 0:1]
    yr = yr.astype(np.float32)
    yr -= (H-1.0)/2.0
    yk = np.exp(-np.power(yr, 2.0)/(2*sigma*sigma))
    image_yk = signal.convolve2d(image_xk, yk, 'same','symm')
    image_conv = image_yk/(2*np.pi*np.power(sigma, 2.0))

    return image_conv

def DoG(image, size, sigma, k=1.1):
    Is = gaussConv(image, size, sigma)
    Isk = gaussConv(image, size, sigma*k)
    doG = Isk - Is
    doG /= (np.power(sigma, 2.0)*(k-1))
    return doG

def zero_cross_default(doG):
    zero_cross = np.zeros(doG.shape, np.uint8);
    rows, cols = doG.shape
    for r in range(1, rows-1):
        for c in range(1, cols-1):
            if doG[r][c-1]*doG[r][c+1] < 0:
                zero_cross[r][c]=255
                continue
            if doG[r-1][c] * doG[r+1][c] <0:
                zero_cross[r][c] = 255
                continue
            if doG[r-1][c-1] * doG[r+1][c+1] <0:
                zero_cross[r][c] = 255
                continue
            if doG[r-1][c+1] * doG[r+1][c-1] <0:
                zero_cross[r][c] = 255
                continue
    return zero_cross

def Marr_Hildreth(image, size, sigma, k=1.1):
    doG = DoG(image, size, sigma, k)
    zero_cross = zero_cross_default(doG)

    return zero_cross

if __name__ == "__main__":
    img_path= r"C:\Users\silence_cho\Desktop\Messi.jpg"
    img = cv2.imread(img_path, 0)
    k = 1.1
    marri_edge = Marr_Hildreth(img, (11, 11), 1, k)
    marri_edge2 = Marr_Hildreth(img, (11, 11), 2, k)
    marri_edge3 = Marr_Hildreth(img, (7, 7), 1, k)

    cv2.imshow("img", img)
    cv2.imshow("marri_edge", marri_edge)
    cv2.imshow("marri_edge2", marri_edge2)
    cv2.imshow("marri_edge3", marri_edge3)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

Mari-Hildreth边缘检测算法

posted @ 2020-09-07 23:27 silence_cho 阅读(7958) 评论(0) 编辑收藏举报

刷新页面返回顶部

silence_cho

(六)OpenCV-Python学习—边缘检测2

公告