学习率调整策略
算是做了一些项目,训练过SSD物体检测模型和CRNN文字识别模型 ,摸索了一段日子,关于如何炼出更好的丹,一直很困惑,总结记录下一些心得吧。感觉整体上可以分为五大块:数据标注和处理,优化算法,学习率更新策略,可视化训练过程, 损失函数优化
1. 数据标注和处理
1.1 数据标注
数据标注过程中,感觉主要有两点需要注意:一是数据标注最好书写一份清晰明了的标注规范,想清楚难正样本,难负样本,易正样本,易负样本的样本定义及分布比例; 二是标注完成后,一定要多花点时间对数据进行检查。在训练SSD物体检测模型时,踩过一些坑,现在我都会对标注框的大小,坐标是否越界图片,标注名称进行批量检查,再人工过一遍。(标注人员手抖,会引入一些几个像素大小的小;标注名称会出现大小写,漏字母;标注坐标会出现负数,大于长宽的异常值)。在训练CRNN文字识别模型时,我现在一般先对标注文字是否在词库进行批量检查,然后用百度OCR或自己的模型对标注文字批量检查,最后在人工过一遍。
还有一点就是,如果训练过程中loss经常出现-Nan,在保证没有引发梯度爆炸的情况下(可以降低学习率,或进行梯度裁剪来保证不发生梯度爆炸),大部分情况下都可能是数据标注的原因,最好检查下数据标注
1.2 数据处理
主要是数据增强和归一化的问题,还没整理好,后面来填坑。。
增强:AlexNet方式数据增强,Resnet和Desnet数据增强方式
2. 优化算法
https://mxnet.cdn.apache.org/api/python/docs/tutorials/packages/optimizer/index.html
https://www.jianshu.com/p/40adad7cb50d
目前常用的优化算法包括SGD+momentum, Nesterov, AdaGrad,RMSProp,AdaDelta, Adam。其中SGD+Momentum, Nesterov为动量更新法,所有参数采用相同的学习率,且不会改变学习率;AdaGrad,RMSProp,AdaDelta为自适应更新法,不同参数采用不同的学习率,且学习率不断减小。Adam为动量和自适应两者的结合。要理解这些算法,最重要的是明白指数加权移动平均(EMA, Exponential Weighted Moving Average)

2.1 指数加权移动平均
EMA是一种近似求平均值的方法,权重为指数。股票K线图中的10日线采用EMA计算的, 指对过去10天股价的加权平均(日期越往前,权重越小)。其数学公式和含义如下:
给定超参数0≤𝛾<1,当前时间步t的变量yt是上一时间步𝑡−1的变量yt−1和当前时间步另一变量xt的线性组合:
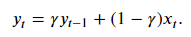
我们可以对yt展开
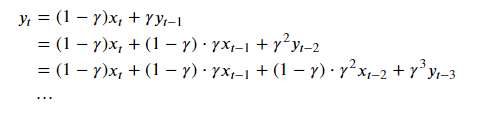
令n=1/(1−γ),那么 (1−1/n)n=γ1/(1−γ)。因为
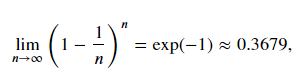
所以当γ→1时,γ1/(1−γ)=exp(−1),如0.9520≈exp(−1)。如果把exp(−1)当作一个比较小的数,我们可以在近似中忽略所有含γ1/(1−γ)和比γ1/(1−γ)更高阶的系数的项。例如,当γ=0.95时,
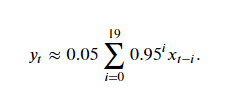
因此,在实际中,我们常常将yt看作是对最近1/(1−γ)个时间步的xt值的加权平均。例如,当γ=0.95时,yt可以被看作对最近20个时间步的xt值的加权平均;当γ=0.9时,yt可以看作是对最近10个时间步的xt值的加权平均。而且,离当前时间步t越近的xt值获得的权重越大(越接近1)。
2.2 SGD+Momentum
理解了指数加权移动平均是对过去时间点数据的加权平均后,再来看SGD+Momentum优化算法的公式:
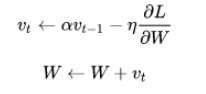
上述式子可以改写为下面形式:
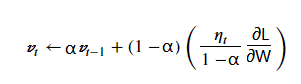 根据指数移动平均值,可以看出Vt是对𝜂𝑡 *∂L/∂W /(1−α) 的移动平均,即当前梯度,是过去梯度的移动加权平均后再除以1-α,且移动周期长度近似为1/(1-α). 这里的α就是所谓的momentum,如下面mxnet中设置momentum为0.9,表示是对过去10个梯度(1/(1-0.9))的加权移动平均,若设为0.95,则是对过去20个梯度。在实际调参过程中,若不同batch的梯度值变化大,即容易抖动,则可以加大momentum的值来平滑梯度;另一方面,若不同batch梯度变化方向相同时,momentum则会起到加速的作用,momentum为0.9则近似梯度值放大了10倍,能加速训练过程。
根据指数移动平均值,可以看出Vt是对𝜂𝑡 *∂L/∂W /(1−α) 的移动平均,即当前梯度,是过去梯度的移动加权平均后再除以1-α,且移动周期长度近似为1/(1-α). 这里的α就是所谓的momentum,如下面mxnet中设置momentum为0.9,表示是对过去10个梯度(1/(1-0.9))的加权移动平均,若设为0.95,则是对过去20个梯度。在实际调参过程中,若不同batch的梯度值变化大,即容易抖动,则可以加大momentum的值来平滑梯度;另一方面,若不同batch梯度变化方向相同时,momentum则会起到加速的作用,momentum为0.9则近似梯度值放大了10倍,能加速训练过程。
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.01, 'momentum': 0.9})
2.3 自适应法
AdaGrad
在SGD中,目标函数自变量的每一个元素在相同时间步都使用同一个学习率来自我迭代。假设目标函数为𝑓,自变量为一个二维向量[𝑥1,𝑥2]⊤,在学习率为𝜂的梯度下降中,元素𝑥1和𝑥2都使用相同的学习率𝜂来自我迭代:
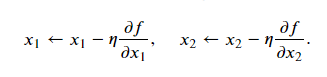 𝑥1和𝑥2的梯度值有较大差别时,需要选择足够小的学习率使得自变量在梯度值较大的维度上不发散(爆炸)。但这样会导致自变量在梯度值较小的维度上迭代过慢。动量法依赖指数加权移动平均使得自变量的更新方向更加一致,从而降低发散的可能。AdaGrad则是对每一个维度采用不同的学习率,避免统一的学习率难以适应所有维度的问题
𝑥1和𝑥2的梯度值有较大差别时,需要选择足够小的学习率使得自变量在梯度值较大的维度上不发散(爆炸)。但这样会导致自变量在梯度值较小的维度上迭代过慢。动量法依赖指数加权移动平均使得自变量的更新方向更加一致,从而降低发散的可能。AdaGrad则是对每一个维度采用不同的学习率,避免统一的学习率难以适应所有维度的问题
在时间步0,AdaGrad将s0中每个元素初始化为0。在时间步t,首先将小批量随机梯度gt按元素平方后累加到变量st:
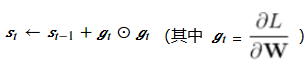
其中⊙是按元素相乘。接着,我们将目标函数自变量中每个元素的学习率通过按元素运算重新调整一下:
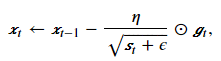
其中𝜂是学习率,𝜖是为了维持数值稳定性而添加的常数,如10−6。这里开方、除法和乘法的运算都是按元素运算的。这些按元素运算使得目标函数自变量中每个元素都分别拥有自己的学习率。例如𝑥t为[𝑥1,𝑥2]⊤, 假设对应的梯度gt为[2, 10]T,则如下公式中(近似表达,分母中还有st-1及其之前等项省略),𝑥1对应的梯度小,但其学习率相对大一点, 𝑥2的梯度大,其学习率对应的梯度相对小一点。这样,AdaGrad就能根据自变量每个维度梯度值的大小来调整各个维度上的学习率。
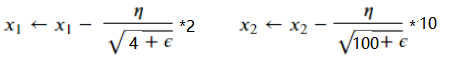
然而,由于st一直在累加按元素平方的梯度,自变量中每个元素的学习率在迭代过程中一直在降低(或不变)。若学习率在迭代早期降得较快且当前解依然不佳时,AdaGrad算法在迭代后期由于学习率过小,可能较难找到一个有用的解。
RMSProp
为了改善AdaGrad学习率一直下降的问题,RMSProp引入了指数加权移动平均。AdaGrad算法里状态变量st是截至时间步t所有小批量随机梯度gt按元素平方和,RMSProp算法将这些梯度按元素平方做指数加权移动平均。具体来说,给定超参数0≤γ<1,RMSProp算法在时间步t>0计算

和AdaGrad算法一样,RMSProp算法将目标函数自变量中每个元素的学习率通过按元素运算重新调整,然后更新自变量
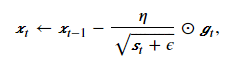
因为RMSProp算法的状态变量st是对平方项𝑔𝑡⊙𝑔𝑡的指数加权移动平均,所以可以看作是最近1/(1−γ)个时间步的小批量随机梯度平方项的加权平均。如此一来,自变量每个元素的学习率在迭代过程中就不再一直降低(或不变)。mxnet中RMSProp算法使用如下所示,gamma1即为上述表达式中的γ,其默认值为0.9,表示对最近10个时间步的随机梯度平方项的加权平均。
from mxnet import gluon, optimizer #optim = optimizer.RMSProp(learning_rate=0.001, gamma1=0.9) trainer = gluon.Trainer(net.collect_params(), optimizer='rmsprop', optimizer_params={'learning_rate':0.001, 'gamma1':0.9})
AdaDelta
AdaDelta和RMSProp一样,也是对AdaGrad的改进,引入了指数移动加权移动平均;不同于RMSProp的是,AdaDelta没有学习率这个参数。给定超参数0≤ρ<1(对应RMSProp算法中的𝛾),在时间步t>0,同RMSProp算法一样计算
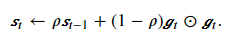
与RMSProp算法不同的是,AdaDelta算法还维护一个额外的状态变量Δxt,其元素同样在时间步0时被初始化为0。我们使用Δxt−1来计算自变量的变化量:

其中ϵ是为了维持数值稳定性而添加的常数,如10−5。接着更新自变量:
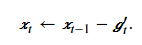
最后,我们使用Δxt来记录自变量变化量gt′按元素平方的指数加权移动平均:
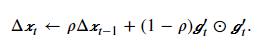
可以看到,如不考虑ϵ的影响,AdaDelta算法与RMSProp算法的不同之处在于使用√Δxt−1来替代超参数𝜂。mxnet中AdaDelta算法使用如下所示,rho即为上述表达式中的ρ,其默认值为0.9,表示对最近10个时间步的随机梯度平方项的加权平均。
from mxnet import gluon, optimizer optim = optimizer.AdaDelta(rho=0.9) trainer = gluon.Trainer(net.collect_params(), optimizer="adadelta", optimizer_params={"rho": 0.9})
2.4 Adam
Adam结合了动量法和自适应法,相当于Momentum+RMSProp。给定超参数0≤β1<1(算法作者建议设为0.9),0≤β2<1(算法作者建议设为0.999),Adam首先计算Vt, St:
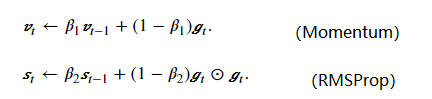
由于指数加权移动平均存在冷启动问题(第一个值初始化为0,导致第二个值,第三个值等前面的值求平均值会偏小),Adam对其进行了修正。即在上面计算中,由于v0和s0初始化为0,当t较小时,过去各时间步小批量随机梯度权值之和会较小。例如当𝛽1=0.9时,𝑣1=0.1𝑔1。为了消除这样的影响,对于任意时间步t,我们可以将vt再除以1−β1t,从而使过去各时间步小批量随机梯度权值之和为1。这也叫作偏差修正。在Adam算法中,我们对变量vt和st均作偏差修正:
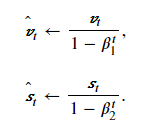
接下来,Adam算法使用以上偏差修正后的变量𝑣̂ 𝑡v^t和𝑠̂ 𝑡s^t,将模型参数中每个元素的学习率通过按元素运算重新调整
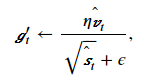
其中𝜂η是学习率,𝜖ϵ是为了维持数值稳定性而添加的常数,如10−810−8。和AdaGrad算法、RMSProp算法以及AdaDelta算法一样,目标函数自变量中每个元素都分别拥有自己的学习率。最后,使用𝑔′𝑡gt′迭代自变量:
在mxnet中,adam优化算法使用如下,其参数中的 beta1=0.9, beta2=0.999 即上诉表达式中的β1,β2,beta1=0.9表示对过去10个时间步的梯度进行加权平均,beta2=0.999表示对过去1000个时间步的梯度平方值进行加权平均。
from mxnet import gluon, optimizer #optim = optimizer.Adam(learning_rate=0.001, beta1=0.9, beta2=0.999) trainer = gluon.Trainer(net.collect_params(), optimizer="adam", optimizer_params={'learning_rate':0.001, 'beta1':0.9, "beta2":0.999})
3. 学习率更新策略
在上述的优化算法中,自适应法会自动来调节学习率的大小;而对于SGD类的学习率训练过程中保持不变,我们自己制定其改变策略,一般随着训练次数的增加都需要降低学习率,比较常见的有三种,一是一定步长衰减一次(步长衰减);二是根据幂函数逐渐降低;三是采用余弦函数逐渐降低(余弦退火)
mxnet的使用如下:
步长衰减:
schedule1= mx.lr_scheduler.FactorScheduler(step=40, factor=0.5, base_lr=0.01) #每隔40个epoch,学习率*0.5 schedule2 = mx.lr_scheduler.MultiFactorScheduler(step=[40, 100, 160], factor=0.5) #第100,250,500个epoch,学习率*0.1
其对应学习率变化图如下:

内部实现很简单,实现源码如下:

class FactorScheduler(LRScheduler): """Reduce the learning rate by a factor for every *n* steps. It returns a new learning rate by:: base_lr * pow(factor, floor(num_update/step)) Parameters ---------- step : int Changes the learning rate for every n updates. factor : float, optional The factor to change the learning rate. stop_factor_lr : float, optional Stop updating the learning rate if it is less than this value. """ def __init__(self, step, factor=1, stop_factor_lr=1e-8, base_lr=0.01, warmup_steps=0, warmup_begin_lr=0, warmup_mode='linear'): super(FactorScheduler, self).__init__(base_lr, warmup_steps, warmup_begin_lr, warmup_mode) if step < 1: raise ValueError("Schedule step must be greater or equal than 1 round") if factor > 1.0: raise ValueError("Factor must be no more than 1 to make lr reduce") self.step = step self.factor = factor self.stop_factor_lr = stop_factor_lr self.count = 0 def __call__(self, num_update): if num_update < self.warmup_steps: return self.get_warmup_lr(num_update) # NOTE: use while rather than if (for continuing training via load_epoch) while num_update > self.count + self.step: self.count += self.step self.base_lr *= self.factor if self.base_lr < self.stop_factor_lr: self.base_lr = self.stop_factor_lr logging.info("Update[%d]: now learning rate arrived at %0.5e, will not " "change in the future", num_update, self.base_lr) else: logging.info("Update[%d]: Change learning rate to %0.5e", num_update, self.base_lr) return self.base_lr

class MultiFactorScheduler(LRScheduler): """Reduce the learning rate by given a list of steps. Assume there exists *k* such that:: step[k] <= num_update and num_update < step[k+1] Then calculate the new learning rate by:: base_lr * pow(factor, k+1) Parameters ---------- step: list of int The list of steps to schedule a change factor: float The factor to change the learning rate. warmup_steps: int number of warmup steps used before this scheduler starts decay warmup_begin_lr: float if using warmup, the learning rate from which it starts warming up warmup_mode: string warmup can be done in two modes. 'linear' mode gradually increases lr with each step in equal increments 'constant' mode keeps lr at warmup_begin_lr for warmup_steps """ def __init__(self, step, factor=1, base_lr=0.01, warmup_steps=0, warmup_begin_lr=0, warmup_mode='linear'): super(MultiFactorScheduler, self).__init__(base_lr, warmup_steps, warmup_begin_lr, warmup_mode) assert isinstance(step, list) and len(step) >= 1 for i, _step in enumerate(step): if i != 0 and step[i] <= step[i-1]: raise ValueError("Schedule step must be an increasing integer list") if _step < 1: raise ValueError("Schedule step must be greater or equal than 1 round") if factor > 1.0: raise ValueError("Factor must be no more than 1 to make lr reduce") self.step = step self.cur_step_ind = 0 self.factor = factor self.count = 0 def __call__(self, num_update): if num_update < self.warmup_steps: return self.get_warmup_lr(num_update) # NOTE: use while rather than if (for continuing training via load_epoch) while self.cur_step_ind <= len(self.step)-1: if num_update > self.step[self.cur_step_ind]: self.count = self.step[self.cur_step_ind] self.cur_step_ind += 1 self.base_lr *= self.factor logging.info("Update[%d]: Change learning rate to %0.5e", num_update, self.base_lr) else: return self.base_lr return self.base_lr
函数衰减:
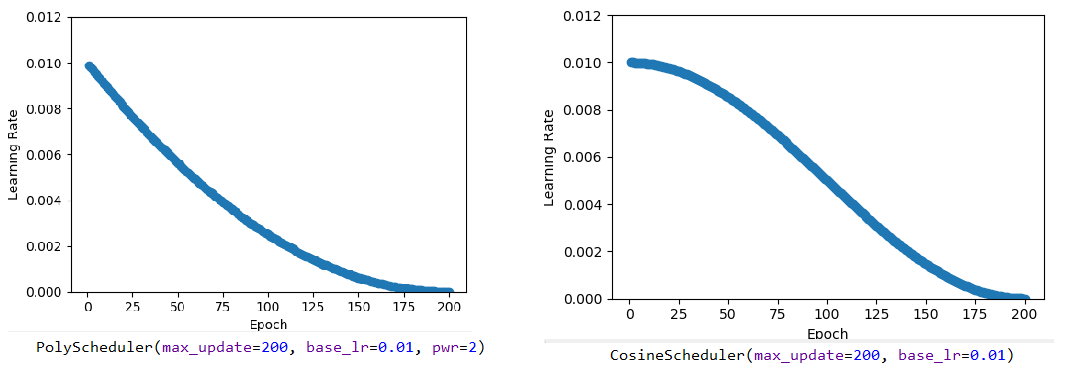
scheduler3 = mx.lr_scheduler.PolyScheduler(max_update=200, base_lr=0.01, pwr=2) #前200次epoch,学习率*(1-epoch/200)^2 scheduler4 = mx.lr_scheduler.CosineScheduler(max_update=200, base_lr=0.01) #前200次epoch, 学习率*(1+cos(epoch*π/200))/2
其对应学习率变化图如下:(一个是按幂函数趋势衰减,一个是按余弦函数趋势衰减)
其内部实现源码如下:

class PolyScheduler(LRScheduler): """ Reduce the learning rate according to a polynomial of given power. Calculate the new learning rate, after warmup if any, by:: final_lr + (start_lr - final_lr) * (1-nup/max_nup)^pwr if nup < max_nup, 0 otherwise. Parameters ---------- max_update: int maximum number of updates before the decay reaches final learning rate. base_lr: float base learning rate to start from pwr: int power of the decay term as a function of the current number of updates. final_lr: float final learning rate after all steps warmup_steps: int number of warmup steps used before this scheduler starts decay warmup_begin_lr: float if using warmup, the learning rate from which it starts warming up warmup_mode: string warmup can be done in two modes. 'linear' mode gradually increases lr with each step in equal increments 'constant' mode keeps lr at warmup_begin_lr for warmup_steps """ def __init__(self, max_update, base_lr=0.01, pwr=2, final_lr=0, warmup_steps=0, warmup_begin_lr=0, warmup_mode='linear'): super(PolyScheduler, self).__init__(base_lr, warmup_steps, warmup_begin_lr, warmup_mode) assert isinstance(max_update, int) if max_update < 1: raise ValueError("maximum number of updates must be strictly positive") self.power = pwr self.base_lr_orig = self.base_lr self.max_update = max_update self.final_lr = final_lr self.max_steps = self.max_update - self.warmup_steps def __call__(self, num_update): if num_update < self.warmup_steps: return self.get_warmup_lr(num_update) if num_update <= self.max_update: self.base_lr = self.final_lr + (self.base_lr_orig - self.final_lr) * \ pow(1 - float(num_update - self.warmup_steps) / float(self.max_steps), self.power) return self.base_lr

class CosineScheduler(LRScheduler): """ Reduce the learning rate according to a cosine function Calculate the new learning rate by:: final_lr + (start_lr - final_lr) * (1+cos(pi * nup/max_nup))/2 if nup < max_nup, 0 otherwise. Parameters ---------- max_update: int maximum number of updates before the decay reaches 0 base_lr: float base learning rate final_lr: float final learning rate after all steps warmup_steps: int number of warmup steps used before this scheduler starts decay warmup_begin_lr: float if using warmup, the learning rate from which it starts warming up warmup_mode: string warmup can be done in two modes. 'linear' mode gradually increases lr with each step in equal increments 'constant' mode keeps lr at warmup_begin_lr for warmup_steps """ def __init__(self, max_update, base_lr=0.01, final_lr=0, warmup_steps=0, warmup_begin_lr=0, warmup_mode='linear'): super(CosineScheduler, self).__init__(base_lr, warmup_steps, warmup_begin_lr, warmup_mode) assert isinstance(max_update, int) if max_update < 1: raise ValueError("maximum number of updates must be strictly positive") self.base_lr_orig = base_lr self.max_update = max_update self.final_lr = final_lr self.max_steps = self.max_update - self.warmup_steps def __call__(self, num_update): if num_update < self.warmup_steps: return self.get_warmup_lr(num_update) if num_update <= self.max_update: self.base_lr = self.final_lr + (self.base_lr_orig - self.final_lr) * \ (1 + cos(pi * (num_update - self.warmup_steps) / self.max_steps)) / 2 return self.base_lr
训练过程中使用如下:
schedule = mx.lr_scheduler.MultiFactorScheduler(step=[40, 100, 160], factor=0.1, base_lr=0.0003) sgd_optimizer = mx.optimizer.SGD(learning_rate=0.03, lr_scheduler=schedule) trainer = mx.gluon.Trainer(params=net.collect_params(), optimizer=sgd_optimizer)
还有一些论文中新出现的策略,可以参考和尝试下,这里主要介绍下两个自认为还实用的策略。一个是循环学习率,一个是学习率warmup
循环学习率
关于循环学习率,主要有两篇文章推荐的比较多。一是2015年发表的Cyclical Learning Rates for Traing Neural Network(CLR), 另外一篇也是2016年发表的文章SGDR:Stochastic Gradient Descent with Warm Restarts ,。
CLR
CLR的主要思想是,设置一个最小学习率(base_lr)和最大学习率(max_lr),训练过程中学习率周期性的在这个区间内取值。其中最简单的一种方式是学习率先从区间下界base_lr线性递增,达到上界max_lr后再线性递减回到下界值,如下图所示:
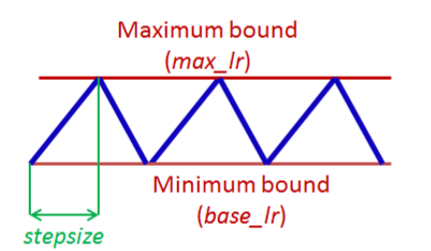
在上图中的每一个周期内,学习率变化曲线是一个三角形,作者也称之为三角学习率调整策略。除此之外,作者还讨论下面的两种稍微复杂一点的策略:
- Triangular2: 同上,不过在于每个周期后,区间的大小减半。
- Exp_range:同上,不过在于每个周期后,区间的上下界按一个指数因子衰减。
这3种方式在实验中并没有绝对的最优,不过与传统的学习率调整策略相比,CLR在多个数据集和多种常用的网络结构上的实验结果都一致的:1)提升了模型的收敛率,加速了训练速度;2)提升了模型的性能,在分类问题上获得了更好的正确率。
CLR有3个超参数需要设置,第一个参数stepsize,表示经过多少个迭代,学习率从base_lr递增到max_lr,即一个周期的一半。作者指出,stepsize这个参数对模型的性能有很好的鲁棒性,一般设置为一个Epoch中迭代数的2-8倍。学习率区间的上下界可以通过一个“LR range test”来估计,首先选取一对上下界(base_lr, max_lr),依学习率从base_lr线性递增到max_lr的策略试训练几个Epoch,最后画出学习率与正确率的曲线图,比如:

在LR range test中,max_lr可以选择为正确率保持平稳,或者开始下降的那个点,base_lr一般设为max_lr的1/3 或者1/4。上图中lr=0.006左右时,准确率不再大幅增加,因此可以设置max_lr=0.006, base_lr = 0.006/4 = 0.0015.
CLR有效的原因: 小的学习率通常不能产生足够大的梯度变化使其跳过鞍点(即使跳过,也需要花费很长时间),而周期性的增大学习率有助于加速逃离鞍点和sharp型的局部最优点。前者可以加速训练过程,后者能使网络收敛到flat型局部最优点,获得更好的鲁棒性。
在mxnet中实现CLR如下(三角学习率调整策略):

class TriangularSchedule(): def __init__(self, min_lr, max_lr, cycle_length, inc_fraction=0.5): """ min_lr: lower bound for learning rate (float) max_lr: upper bound for learning rate (float) cycle_length: iterations between start and finish (int) inc_fraction: fraction of iterations spent in increasing stage (float) """ self.min_lr = min_lr self.max_lr = max_lr self.cycle_length = cycle_length self.inc_fraction = inc_fraction def __call__(self, iteration): iteration = iteration%self.cycle_length if iteration <= self.cycle_length*self.inc_fraction: unit_cycle = iteration * 1 / (self.cycle_length * self.inc_fraction) elif iteration <= self.cycle_length: unit_cycle = (self.cycle_length - iteration) * 1 / (self.cycle_length * (1 - self.inc_fraction)) else: unit_cycle = 0 adjusted_cycle = (unit_cycle * (self.max_lr - self.min_lr)) + self.min_lr return adjusted_cycle
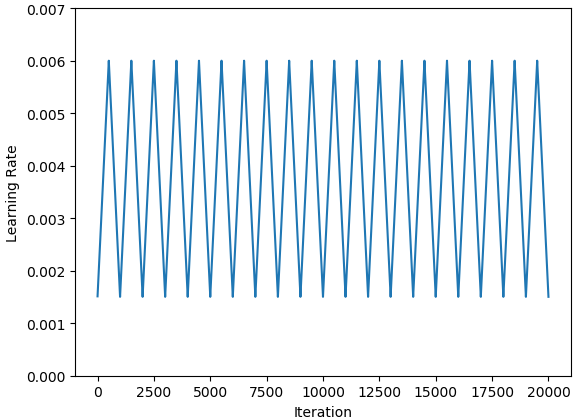
schedule = TriangularSchedule(min_lr=0.0015, max_lr=0.006, cycle_length=1000, inc_fraction=0.5): 表示学习率变化区间为0.0015-0.006,步长stepsize=1000*0.5=500, 其对应的学习率变化曲线如下:
快照集成:https://zhuanlan.zhihu.com/p/93648558
warmup + 余弦退火
https://www.zhihu.com/question/63152097/answer/759214147
测试代码:
import math
import matplotlib.pyplot as plt
import mxnet as mx
from mxnet.gluon import nn
from mxnet.gluon.data.vision import transforms
import numpy as np
def plot_schedule(schedule_fn, iteration=1000):
# Iteration count starting at 1
iterations = [i+1 for i in range(iteration)]
lrs = [schedule_fn(i, end_cosine=iteration) for i in iterations]
plt.scatter(iterations, lrs)
plt.xlabel("Iteration")
plt.ylabel("Learning Rate")
plt.show()
# 前200此迭代采用恒定学习率,200-1000之间采用余弦衰减学习率
def schedule_fn(epoch, start_cosine=200, end_cosine=1000):
final_lr = 0
base_lr_orig = 0.01
if epoch >= start_cosine:
lr = final_lr + (base_lr_orig - final_lr) * \
(1 + math.cos(math.pi * (epoch - start_cosine) / (end_cosine-start_cosine))) / 2
else:
lr = base_lr_orig
return lr
plot_schedule(schedule_fn, 1000)
warmup 预热学习率
带重启的SGD算法 Stochastic Gradient Descent with Warm Restarts
周期性学习率论文 Cyclical Learning Rates for Training Neural Networks
https://www.jiqizhixin.com/articles/nn-learning-rate
https://www.jeremyjordan.me/nn-learning-rate/
https://lumingdong.cn/setting-strategy-of-gradient-descent-learning-rate.html
mixup mixup: Beyond Empirical Risk Minimization (数据增强)
knowledge distillation Distilling the knowledge in a neural network (知识蒸馏)
label smooth Szegedy等人提出了inception v2的模型(论文:Rethinking the inception architecture for computer vision.)。其中提到了Label Smoothing技术,https://www.cnblogs.com/mfryf/p/11381448.html




 浙公网安备 33010602011771号
浙公网安备 33010602011771号