ctc原理理解(转载)
本文大量摘抄和节选于下列文章:
https://zhuanlan.zhihu.com/p/108547594
https://lipengwei.github.io/2018/08/10/CTC原理/
https://blog.csdn.net/JackyTintin/article/details/79425866
1 CTC loss出现的背景
在图像文本识别、语言识别的应用中,所面临的一个问题是神经网络输出与ground truth的长度不一致,这样一来,loss就会很难计算,举个例子来讲,如果网络的输出是”-sst-aa-tt-e'', 而其ground truth为“state”,那么像之前经常用的损失函数如cross entropy便都不能使用了,因为这些损失函数都是在网络输出与ground truth的长度一致情况下使用的。除了长度不一致的情况之外,还有一个比较难的点在于有多种情况的输出都对应着ground truth,根据解码规则(相邻的重复字符合并,去掉blank), path1: "-ss-t-a-t-e-" 和path2: "--stt-a-tt-e"都可以解码成“state”,与ground truth对应, 也就是many-to-one。为了解决以上问题,CTC loss就产生啦~
2 CTC loss原理
2.1 前序
在说明原理之前,首先要说明一下CTC计算的对象:softmax矩阵,通常我们在RNN后面会加一个softmax层,得到softmax矩阵,softmax矩阵大小是timestep*num_classes, timestep表示的是时间序列的维度,num_class表示类别的维度
import numpy as np ts = 12 num_classes = 26+1 #26 for the number of english character, 1 for blank rnn_output = np.random.random((ts, 16))#16 for hidden node number w = np.random.random((16,num_classes)) logits = np.matmul(rnn_output,w)#logits: ts*num_classes=[12,27] #calculate softmax matrix maxvalue = np.max(logits, axis=1, keepdims=True) exp = np.exp(logits-maxvalue) #minus maxvalue for avoiding overflow exp_sum = np.sum(exp, axis=1, keepdims=True) y = softmax = exp/exp_sum #softmax:ts*num_classes=[12,27]
2.2 forward-backward计算
其实呢,整体过程可以看做是对输入的y也就是softmax做了相应的映射得到解码结果,在希望解码结果尽量正确的情况下(使用概率来衡量),对网络的参数进行梯度下降。
在接下来的说明中,我们使用 表示网络的输入,使用
表示softmax矩阵,其大小为timestep*num_classes, 表示的是在第t个timestep时,第k个类别的softmax值, 使用
表示路径, 路径中包含字符, 使用
表示字符集,如果是英文的话,那么一共就有26+1=27类, 使用T表示总的timestep,即时序数。定义一个映射
表示解码过程中many-to-one的映射,就如上面所说的
在给定输入的情况下,输出路径的概率可以表示为:

上述公式的一个假设是:每个时序的字符都是相互独立的,与上下文无关
以上述"state"为例子,可以通过映射得到 "state"的路径集合使用
表示,那么:

上面所说的path1: "-ss-t-a-t-e-" 和path2: "--stt-a-tt-e"都属于路径集合 。
知道了 之后,肯定希望它的概率越大越好,如果取反的话,可以作为损失函数来进行求导,从而反向传播,对参数进行更新啦。
在第t个timestep,对k个类别的softmax值求偏导,即为 ,一个更具体的例子来说就是在第7个timestep, 对类别a的进行求导
,那么

只有在timestep=7时为a的路径才会使用 进行路径的分数计算,所以求偏导的时候只对这部分路径求导就可以啦
path1:"-ss-t-a-t-e-" 第7个timestep为a, path2: "--stt-a-tt-e"第7个timestep也为a, 以a为中点,将这两条路径分别分成两段。
path1_forward: "-ss-t-" path1_backward: "-t-e-"
path2_forward: "--stt-" path2_backward: "-tt-e"
你也会发现 path1_forward+"a"+path2_backward也能够解码成正确的”state", 我们使用path3来表示该路径 , 同样的, path2_forward+"a"+path1_backward也可以解码成正确的“state",我们使用path4表示该路径
在下式中我们考虑中仅仅包含path1,path2, path3, path4
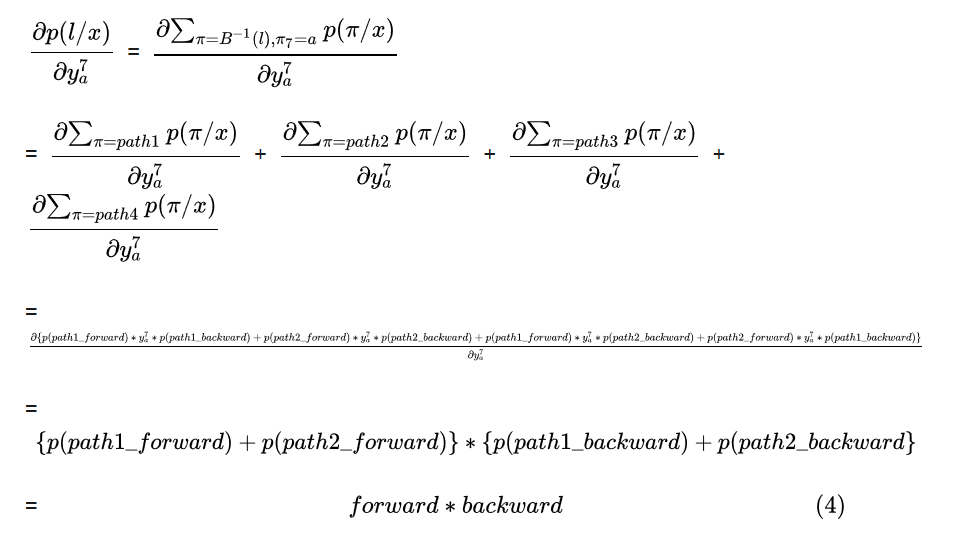
其中, ,
是不是感觉比较简单呢 ~ 因为上面的公式特别复杂,想用符号来表示forward和backward, 用 来表示forward的部分,
表示backward的部分吧
表示将1-t个timestep解码成中的1-s个字符,看公式比较好理解哈
表示将t-T个timestep解码成中的s-|
个字符,
其中表示的是解码后的长度。先看forward部分
2.2.1 forward部分
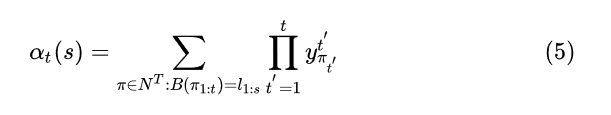
这个公式计算的是所有能够解码成的概率,
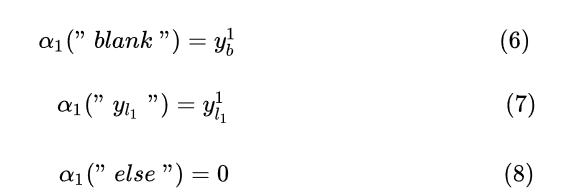
上面三个式子是说第一个timestep的解码成”blank“的概率是 , 解码成
中第一个字符的概率是
, 其他的字符的概率为0, 可以这样理解,如果路径能够解码成正确的”state", 那么第一个timestep的肯定是blank或者"s", 只有这样才能解码正确。在前向和后向计算中,CTC会将blank插入到输出字符串,比如“state”就会变成“-s-t-a-t-e-", 使用
表示。 根据上面的叙述,可以得到如下递推式:
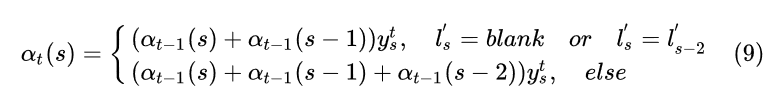
公式可能一下子不能理解透,举个例子好啦,先看上面的那种情况,也就是特殊情况下的递推公式:
假设在第t个timestep解码成 “-s-t-"( ),在第t-1个timestep中,当前的解码只可能是 “-s-t-"
或者“-s-t" (
), 只有这样才能正确解码。“-s-t-" 加入第t个timestep中的blank,会变成”-s-t--", 合并两个相邻的blank变成“-s-t-"。 “-s-t"加入第t个timestep中的blank会变成”-s-t-"。两者去掉空格都可以变成正确的“st"。
假设在第t个timestep解码成 “-s-e-e"( ),在第t-1个timestep中,当前的解码只可能是 “-s-e-"
或者“-s-e" (
), 只有这样才能正确解码。“-s-e-" 加入第t个timestep中的"e",会变成”-s-e-e", 去掉blank会解码成正确的”see“。 “-s-e"加入第t个timestep中的"e"会变成”-s-ee", 去掉blank也会解码成正确的”see“。
公式(9)上面 的情况已经讲完啦,接着我们看公式(9)下面 的情况,也就是普通情况下的递推公式:
假设在第t个timestep解码成 “-s-t-a"( ),在第t-1个timestep中,当前的解码只可能是 “-s-t-a"
或者“-s-t-" (
)再或者“-s-t" (
), 只有这样才能正确解码。“-s-t-a" 加入第t个timestep中的“a“,会变成”-s-t-aa", 合并两个相邻的"a"变成“-s-t-a", 去掉blank可以解码成“sta"。 “-s-t-"加入第t个timestep中的a会变成”-s-t-a",去掉blank可以解码成“sta" 。“-s-t"加入第t个timestep中的a会变成”-s-ta",去掉blank可以解码成“sta"。
forward部分代码理解:
# y表示RNN的特征输出, labels是带空格的 # 例如:labels = [0, 3, 0, 3, 0, 4, 0] # 0 for blank # y的shape=[T, V], labels的长度L=len(label) + len(blank) # 通常来说,L = 2*len(label) + 1 def forward(y, labels): T, V = y.shape L = len(labels) alpha = np.zeros([T, L]) # init alpha[0, 0] = y[0, labels[0]] alpha[0, 1] = y[0, labels[1]] for t in range(1, T): for i in range(L): s = labels[i] a = alpha[t - 1, i] if i - 1 >= 0: a += alpha[t - 1, i - 1] if i - 2 >= 0 and s != 0 and s != labels[i - 2]: a += alpha[t - 1, i - 2] alpha[t, i] = a * y[t, s] return alpha
2.2.2 backward部分
forward讲清楚之后, backward快速的过一遍就好啦
这个公式计算的是所有能够解码成的概率,
上面三个式子是说第T个timestep的解码成”blank“的概率是 , 解码成中第一个字符的概率是
, 其他的字符的概率为0, 可以这样理解,如果路径能够解码成正确的”state", 那么第T个timestep的肯定是blank或者"e", 只有这样才能解码正确。 我们可以得到与forward相似的递推式:
套用上面forward的方式去理解,应该不难的~
backward部分代码理解:
def backward(y, labels): T, V = y.shape L = len(labels) beta = np.zeros([T, L]) # init beta[-1, -1] = y[-1, labels[-1]] beta[-1, -2] = y[-1, labels[-2]] for t in range(T - 2, -1, -1): for i in range(L): s = labels[i] a = beta[t + 1, i] if i + 1 < L: a += beta[t + 1, i + 1] if i + 2 < L and s != 0 and s != labels[i + 2]: a += beta[t + 1, i + 2] beta[t, i] = a * y[t, s] return beta
2.3 梯度
求了上面的forward和backward之后,就可以求解梯度啦

根据 可以得到
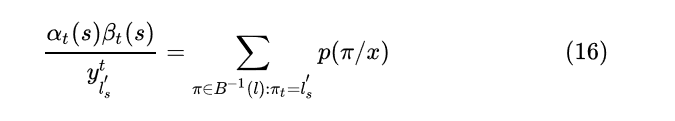
因为
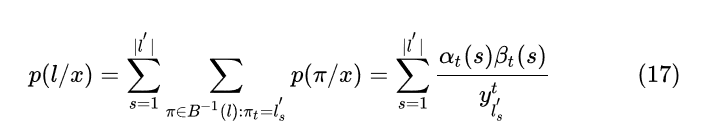
所以对求导的话, 仅有当为类别k的那一项不为0, 其余项的偏导都为0
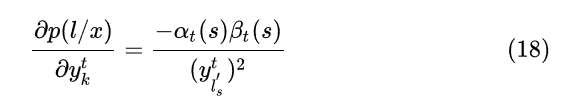
一般我们优化似然函数的对数,因此,梯度计算如下:
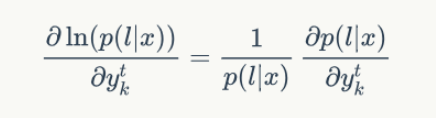
其中,似然值p(l|x)在前向计算中已经求得,就是最后输出为 blank 或者 最后一个| l' |的前向概率值: (末尾带有blank和不带有blank的,“-s-t-a-t-e-"和"-s-t-a-t-e"都可以正确解码,所以)
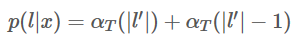
代码表示就是:

梯度计算的代码理解:
# y是RNN的输入, labels为加空格的标签 def gradient(y, labels): T, V = y.shape L = len(labels) alpha = forward(y, labels) beta = backward(y, labels) p = alpha[-1, -1] + alpha[-1, -2] grad = np.zeros([T, V]) for t in range(T): for s in range(V): # 输出 s = l 标签的集合 lab = [i for i, c in enumerate(labels) if c == s] for i in lab: grad[t, s] += alpha[t, i] * beta[t, i] grad[t, s] /= y[t, s] ** 2 grad /= p return grad
3. 解码
训练后的 Nw 可以用来预测新的样本输入对应的输出字符串,这涉及到解码。 按照最大似然准则,最优的解码结果为:
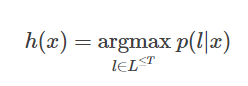
然而,上式不存在已知的高效解法。下面介绍几种实用的近似破解码方法。
3.1 贪心搜索 (greedy search)
我们放弃寻找使 p(l|x)最大的字符串,退而寻找一个使 p(π|x) 最大的字符串,即
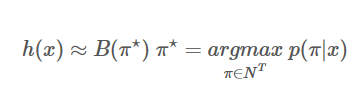
简化后,解码过程(构造 π⋆)变得非常简单(基于独立性假设): 即在每个时刻输出概率最大的字符:

# 输出删除blank def remove_blank(labels, blank=0): new_labels = [] # e.g. [-,a,a,-,-,p,p,-,-,p,p,-,-,l,l,-,e,e,-,] # combine duplicate previous = None for l in labels: if l != previous: new_labels.append(l) previous = l # remove blank new_labels = [l for l in new_labels if l != blank] return new_labels # 贪心搜索 def greedy_decode(y, blank='-'): raw_rs = np.argmax(y, axis=1) rs = remove_blank(raw_rs, blank) return raw_rs, rs
3.2 束搜索(Beam Search)
贪心搜索的性能非常受限。例如,它不能给出除最优路径之外的其他其优路径。很多时候,如果我们能拿到nbest的路径,后续可以利用其他信息来进一步优化搜索的结果。束搜索能近似找出 top 最优的若干条路径。
def beam_decode(y, beam_size=10): T, V = y.shape log_y = np.log(y) beam = [([], 0)] for t in range(T): # for every timestep new_beam = [] for prefix, score in beam: for i in range(V): # for every state new_prefix = prefix + [i] new_score = score + log_y[t, i] new_beam.append((new_prefix, new_score) \ \ ) # top beam_size new_beam.sort(key=lambda x: x[1], reverse=True) beam = new_beam[:beam_size] return beam
3.3 前缀束搜索(Prefix Beam Search)
直接的束搜索的一个问题是,在保存的 top N 条路径中,可能存在多条实际上是同一结果(经过去重复、去 blank 操作)。这减少了搜索结果的多样性。下面介绍的前缀搜索方法,在搜索过程中不断的合并相同的前缀[2]。参考 gist,前缀束搜索实现如下:
from collections import defaultdict def prefix_beam_decode(y, beam_size=10, blank=0): T, V = y.shape log_y = np.log(y) beam = [(tuple(), (0, ninf))] # blank, non-blank for t in range(T): # for every timestep new_beam = defaultdict(lambda : (ninf, ninf)) for prefix, (p_b, p_nb) in beam: for i in range(V): # for every state p = log_y[t, i] if i == blank: # propose a blank new_p_b, new_p_nb = new_beam[prefix] new_p_b = logsumexp(new_p_b, p_b + p, p_nb + p) new_beam[prefix] = (new_p_b, new_p_nb) continue else: # extend with non-blank end_t = prefix[-1] if prefix else None # exntend current prefix new_prefix = prefix + (i,) new_p_b, new_p_nb = new_beam[new_prefix] if i != end_t: new_p_nb = logsumexp(new_p_nb, p_b + p, p_nb + p) else: new_p_nb = logsumexp(new_p_nb, p_b + p) new_beam[new_prefix] = (new_p_b, new_p_nb) # keep current prefix if i == end_t: new_p_b, new_p_nb = new_beam[prefix] new_p_nb = logsumexp(new_p_nb, p_nb + p) new_beam[prefix] = (new_p_b, new_p_nb) # top beam_size beam = sorted(new_beam.items(), key=lambda x : logsumexp(*x[1]), reverse=True) beam = beam[:beam_size] return beam np.random.seed(1111) y = softmax(np.random.random([20, 6])) beam = prefix_beam_decode(y, beam_size=100) for string, score in beam[:20]: print(remove_blank(string), score)
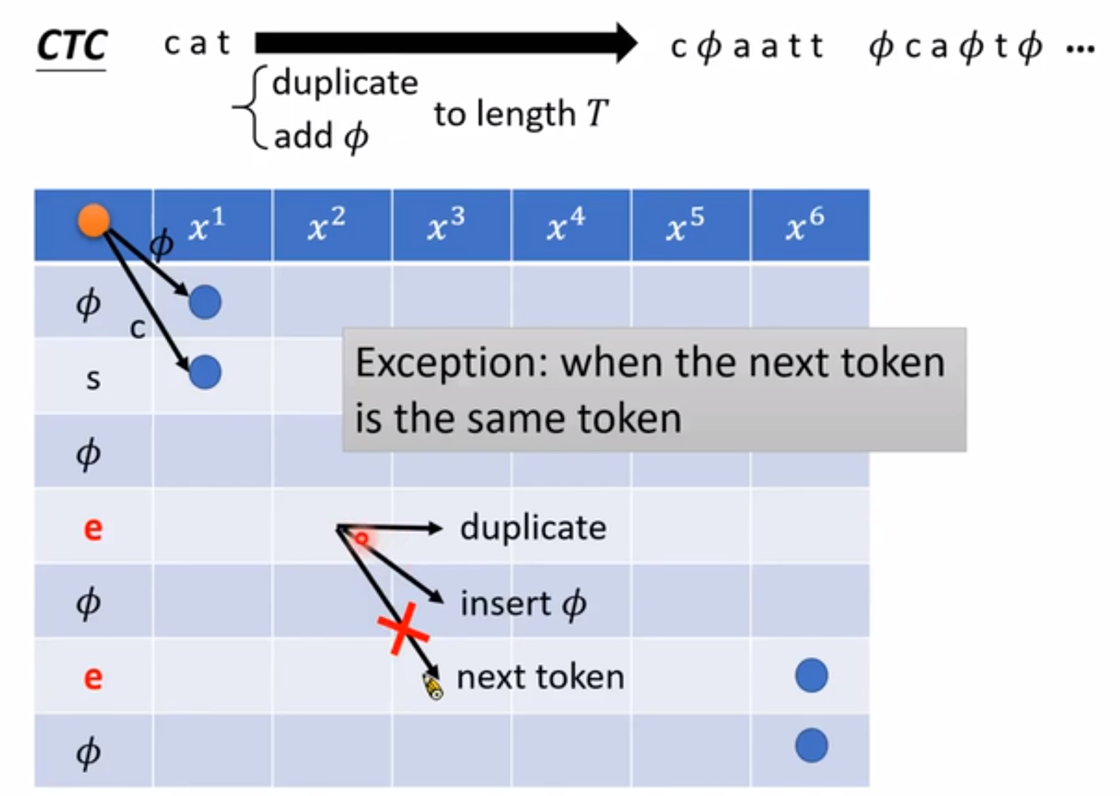
4. 补充
关于CTC的forward递推公式,找到几张示意图,可以方便记忆。下图中cat是真实的标签序列,模型输出是序列:x1x2x3x4x5x6, 将真实标签填充为序列:∅c∅a∅t∅, 下图中是将这两个序列进行对齐的示意图,就是类似于寻找动态规划中的状态转移方程。