样本不均衡问题
one-stage的检测精度比不上two-stage,一个主要原因是训练过程样本不均衡造成。样本不均衡主要包括两方面,一是正负样本的不均衡;二是难易样本的不均衡。目前解决这类问题主要是两种方案(见综述Imbalance Problems in Object Detection: A Review):一是hard sampling方法,从所有样本中选择一定量的正样本和负样本,只有被选择的样本才计算loss,一般会倾向选择一些难负例样本,比如OHEM;另外一类方法是soft sampling方法,选择所有样本计算loss,但是不同的样本赋给不同的权重值,比如focal loss。这里学习下OHEM,S-OHEM,Focal Loss,A-fast-RCNN,GHM(梯度均衡化)。
1. 样本不均衡问题
1.1 正负样本不均衡(负样本主导loss)
在一张图片中,检测目标只占少部分,其他部分都是背景。实际训练过程中,往往会选择与检测目标box的IOU超过0.5的box作为正样本,与检测目标box的IOU少于0.5的作为负样本,必然会造成一张图片中分负样本数量远远超过正样本,即所谓的正负样本不平衡问题。训练过程中一般会控制一个batch中正负样本的比例保持在1:3
1.2. 难易样本不均衡(易样本主导loss)
根据难易和正负样本,可以将样本分成如下四类。难样本的loss大,但数量少,易样本的loss小,但数量多,loss被易样本主导,从难样本上学习的少。
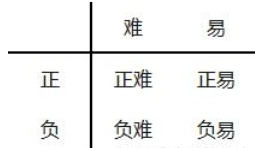
A、易分正样本:容易正确分类的正样本,单个loss小,数量多,累计Loss大。 B、易分负样本:容易正确分类的负样本,单个loss小,数量多,累计Loss大。 C、难分正样本:错分成负样本的正样本,单个loss大,数量少,累计Loss小。 D、难分负样本:错分成正样本的负样本,单个loss大,数量少,累计Loss小
2.样本不均衡解决方案
2.1 OHEM (Online hard example mining, 在线难例挖掘)
OHEM是2016 年的文章Training Region-based Object Detectors with Online Hard Example Mining 提出,在每次产生的所有样本的loss,OHEM将所有负样本按loss大小进行排序,然后根据正负样本1:3的比例去选取loss最大的负样本。比如某个batch中共有1000个样本,正样本有50个,负样本有950个,OHEM会将这从这950个负样本挑150个loss最大的样本做为负样本,其他800个负样本的loss重置为0。这样这个batch的loss由50个正样本和150个负样本组成,维持了正负样本比例, 另外OHEM挑选的是loss最大的150个负样本,150个负样本大部分是难负样本,少部分是易负样本,解决了负样本中易负样本loss主导问题。
简单总结下OHEM的优点:
A. 控制了正负样本的比例为1:3
B. 负样本中难样本loss主导
实际使用中注意点:
A. 正负样本比例设置,1:3是否合适?
B. OHEM将大部分易负样本的loss设置为0,是否过于粗暴?
(S-OHEM)
2.2 Focal Loss
Focal loss是2017年的文章Focal Loss for Dense Object Detection中提出,Focal loss主要对交叉熵损失函数进行了改进,解决难负样本不平衡问题。
交叉熵公式如下:

首先,为了解决难负样本不均衡,focal loss的思想是引入一个表达式,使难样本的loss进一步增加,负样本的loss进一步降低,其表达式如下:
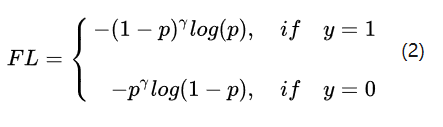
难分正样本预测概率值p较小,假设p=0.1, -log(p)=2.3026; 当γ=2时,-(1-p)γlog(p) =1.8651
易分正样本预测概率值p较大, 假设p=0.9, -log(p)=0.1054; 当γ=2时,-(1-p)γlog(p) =0.001054
对比可以发现,难分正样本loss减小很少,易分正样本loss降低100倍;对于负样本的难易样本也类似,从而起到了解决难易样本不平衡时,易样本loss主导的问题。
其次,为了解决正负样本不均衡,focal loss还引入了一个系数来平衡正负样本不均衡,其表达式如下:
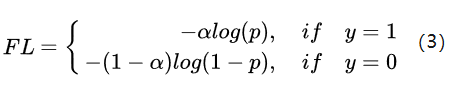
需要注意的是,如果只看这个表达式,α应该设置为0.75, 这样α/(1-α)近似为1:3,能起到平衡作用;但由于-(1-p)γ的影响,实际设置并不是如此。
综合表达式(2)和表达式(3), focal loss的综合表达式是:
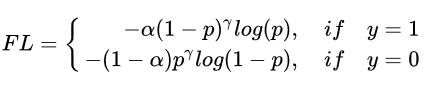
论文中表明 γ=2, α=0.25时效果最好,因为γ太大,使负样本的loss降低太多了,所以 α设置的较小,使正样本的loss相对降低一点。可以仔细体味下下面这个表格,通过focal loss,使训练过程关注对象的排序为正难>负难>正易>负易

2.3 Gradient Harmonizing mechanism(梯度均衡机制)
Focal Loss虽然有很好的效果,但是存在两个问题:
A. Focal loss中的两个超参需要精细的调整,除此之外,它也是一个不会随着数据分布变化的静态loss
B. 如果样本中有离群点(outliers),可能模型已经收敛了但是这些离群点还是会被判断错误,让模型去关注这样的样本,会影响模型的鲁棒性
Gradient Harmonizing mechanism是2019年的论文Gradient Harmonized Single-stage Detector中提出的,解决了上述两个问题。
难易样本的loss差别较大,其实质是训练过程中梯度大小的差别,因此作者对样本梯度的分布进行了统计,定义了一个梯度模长g, 其中p是模型预测的概率,p*是ground-truth的标签。
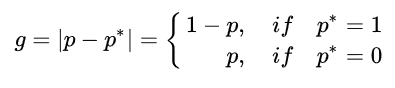
由表达式可以发现,g正比于检测样本的难易程度,g越大则检测难度越大。(如对于正样本,p*=1, 若样本越难,预测概率p越小,其模长g越大)
其推导如下:
我们在计算分类损失时:假设模型输出x,对其进行sigmoid得到预测概率p,再计算交叉熵。因此梯度模长就是交叉熵梯度的绝对值,如下表达式:
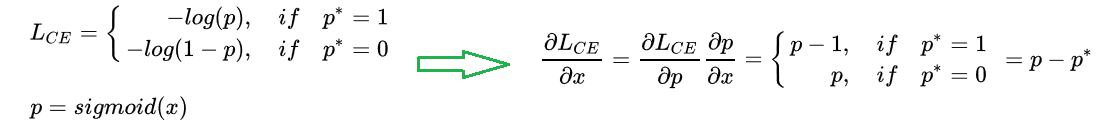
注意sigmoind函数的导数公式: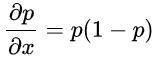
梯度模长g和样本数量之间的分布统计图如下:

可以看到,梯度模长接近于0的样本数量最多,随着梯度模长的增长,样本数量迅速减少,但是在梯度模长接近于1时,样本数量也挺多。
GHM的想法是,我们确实不应该过多关注易分样本,但是特别难分的样本(outliers,离群点)也不该关注!这些离群点的梯度模长d要比一般的样本大很多,如果模型被迫去关注这些样本,反而有可能 降低模型的准确度!况且,这些样本的数量也很多!那怎么同时衰减易分样本和特别难分的样本呢? 太简单了,谁的数量多衰减谁呗!那怎么衰减数量多的呢?简单啊,定义一个变量,让这个变量能衡量出一定梯度范围内的样本数量——这不就是物理上密度的概念吗?于是,作者定义了梯度密度:

表明了样本1~N中,梯度模长分布在
范围内的样本个数,
代表了
区间的长度。因此梯度密度的含义:单位梯度模长g部分的样本个数。
最终,GHM得出进行分类的损失函数如下:
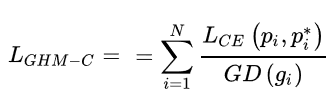
即交叉熵除以梯度密度,梯度密度大的loss会被抑制,易分样本和特别难的样本都被抑制了,从而起到了样本均衡的作用。下图中左边是交叉熵CE,focal loss(FL) 和GHM的单个样本梯度修正,右图是整体样本对于模型训练梯度的贡献。可以发现:候选样本中的简单负样本和非常困难的异常样本的权重都会被降低,即loss会被降低,对于模型训练的影响也会被大大减小。正常困难样本的权重得到提升,这样模型就会更加专注于那些更为有效的正常困难样本,以提升模型的性能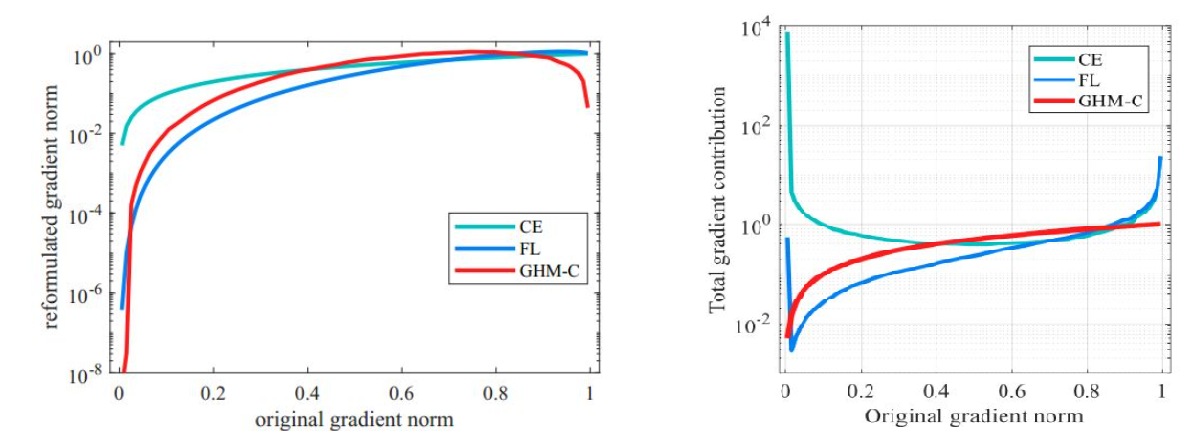
上述GHM用于分类损失,论文中作者还将其用于坐标回归损失,坐标回归loss常用smooth_l1,如下所示
其中 表示模型预测坐标偏移量,
表示anchor实际坐标偏移量,
表示
的函数分界点,常取1/2。定义
,则
的梯度求导为:
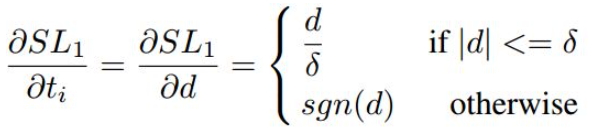
其中sgn表示符号函数。可以看出对于 的所有样本梯度绝对值都为1,这使我们无法通过梯度来区分样本,同时d理论上可以到无穷大。所以论文对
进行变形,计算方法及梯度求导如下所示:
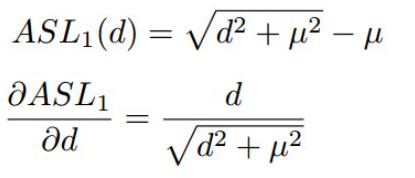
与
的性质很相似,当d较大时都近似为L1 loss,d较小是都近似为L2 loss,而且
的范围在[0,1),适合采用RU方法,在实际使用中,采用μ=0.02。定义梯度的绝对值gr为
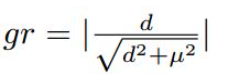
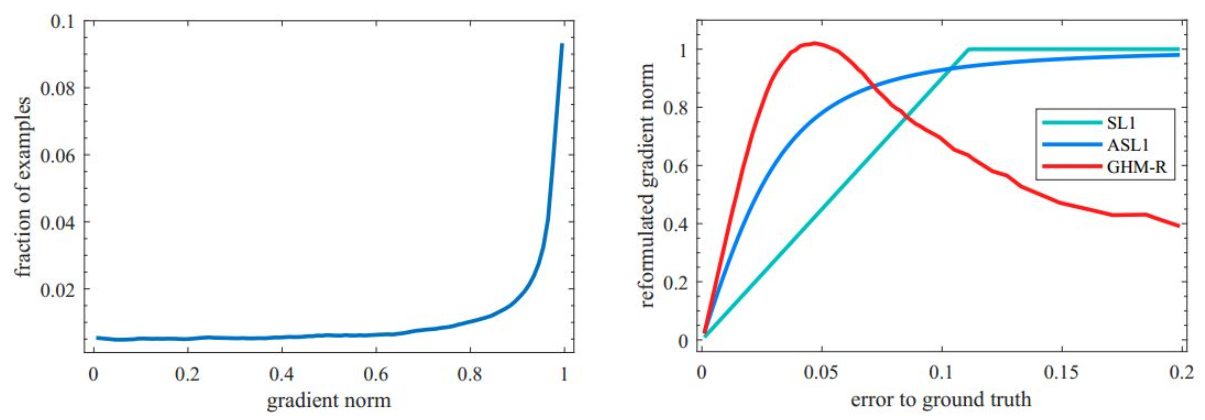
于是我们可以基于gr统计样本坐标回归偏移量的梯度分布情况如下图四所示。由于坐标回归都是正样本,所以简单样本的数量相对并不是很多。而且不同于简单负样本的分类对模型起反作用,简单正样本的回归梯度对模型十分重要。下图左边是梯度统计,可以看出存在相当数量的异常样本的回归梯度值很大。下图右边是修正后梯度,可以看出,GHM-R loss加大了简单样本和正常困难样本的权重,大大降低了异常样本的权重,使模型的训练更加合理
所以使用GHM的思想来修正loss函数,可以得到
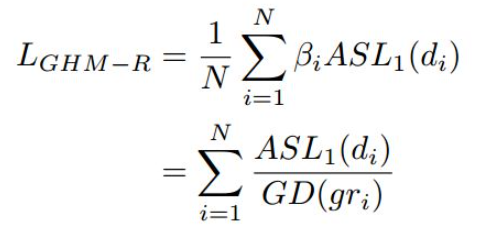
参考:
https://zhuanlan.zhihu.com/p/93658728
https://zhuanlan.zhihu.com/p/269745487
https://www.cnblogs.com/king-lps/p/9497836.html
https://zhuanlan.zhihu.com/p/80594704
https://www.cnblogs.com/leebxo/p/11299697.html
https://zhuanlan.zhihu.com/p/71654647



