pytorch基础学习（二）

　　在神经网络训练时，还涉及到一些tricks，如网络权重的初始化方法，优化器种类（权重更新），图片预处理等，继续填坑。

1. 神经网络初始化（Network Initialization ）

　　1.1 初始化原因

　　　　我们构建好网络，开始训练前，不能默认的将所有权重系数都初始化为零，因为所有卷积核的系数都相等时，提取特征就会一样，反向传播时的梯度也会存在对称性，网络会退化会线性模型。另外网络层数较深时，初始化权重过大，会出现梯度爆炸，而过小又会出现梯度消失。一般权重初始化时需要考虑两个问题：

　　　　（1）权重参数全部相同时，会有梯度更新对称性问题（详细见https://www.zhihu.com/question/36068411?sort=created）

　　　　　　　　如下图中w，b系数都相同时，a1，a2，a3的值也会相同，反过来进行梯度更新时，w，b也是按相同的速率在更新。（不管是哪个神经元，它的前向传播和反向传播的算法都是一样的，如果初始值也一样的话，不管训练多久，它们最终都一样，都无法打破对称（fail to break the symmetry）,那每一层就相当于只有一个神经元，最终L层神经网络就相当于一个线性的网络，如Logistic regression）

　　　　（2）采用饱和激活函数时，进行随机初始化时，权重分布会使神经元输出处于激活函数的梯度饱和区域。

　　　　　　（详细见：https://www.jianshu.com/p/03009cfdf733）

　　1.2 初始化方法

　　　　常用初始化方法有Gaussain initialization， Xavier initialization， Kaiming(MSRA) initialization 。pytorch的torch.nn.init模块中包含了常用的初始化函数。

　　　　Gaussian initialization: 采用高斯分布初始化权重参数

　　　　　　nn.init.normal_(tensor, mean=0, std=1) 能实现不同均值和标准差的高斯分布

　　　　　　nn.init.unoform_(tensor, a=0, b=1) 能实现（a, b）范围内的均匀分布　　　

import torch
import torch.nn as nn
w = torch.empty(3, 5)
nn.init.uniform_(w, a=0, b=1)      #初始化为（0, 1）范围内的均匀分布
nn.init.normal_(w, mean=0, std=1)  #初始化为均值为0， 标准差为1的正态分布
nn.init.constant_(w, 0.3)          # 全部初始化为常量值0.3
nn.init.eye_(w)                     # 初始化为单位矩阵(对角线为1)
print(w)

　　　　Xavier Initialization：均值为0，标准差根据输入神经元和输出神经元的参数个数决定，适合采用tanh和sigmoid等激活函数的模型，详细见下面论文

　　　　　　　　论文：Understanding the difficulty of training deep feedforward neural networks

　　　　　　　　nn.init.xavier_uniform_(tensor, gain=1): 根据xavier，实现了（-a, a）范围内的均匀分布，其中a的计算公式如下：

　　　　　　　　　　　　　　　　　　　　　　　　gain：增益，可以理解为缩放倍数，

　　　　　　　　　　　　　　　　　　　　　　　　fan_in: in_channel*Kw*Kh (输入channel个数， kernel的宽和高)

　　　　　　　　　　　　　　　　　　　　　　　　fan_out: out_channel*Kw*Kh (输出channel个数， kernel的宽和高)

　　　　　　　　nn.init.xavier_normal_(tensor, gain=1): 根据xavier，实现了mean=0, std=std 的高斯分布，其中std的计算公式如下：

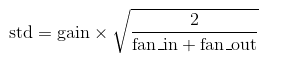
w = torch.empty(3, 3, 5, 5)          #fan_in=75, fan_out=75
nn.init.xavier_uniform_(w, gain=1)   #初始化为（-sqrt(6/150), sqrt(6/150)）范围内的均匀分布
nn.init.xavier_normal_(w, gain=1)    #初始化为mean=0, std=sqrt(2/150)的正态分布

　　　　　　关于fan_in和fan_out的计算方式，pytorch的实现代码如下：

def _calculate_fan_in_and_fan_out(tensor):
    dimensions = tensor.ndimension()
    if dimensions < 2:
        raise ValueError("Fan in and fan out can not be computed for tensor with fewer than 2 dimensions")

    if dimensions == 2:  # Linear
        fan_in = tensor.size(1)
        fan_out = tensor.size(0)
    else:
        num_input_fmaps = tensor.size(1)
        num_output_fmaps = tensor.size(0)
        receptive_field_size = 1
        if tensor.dim() > 2:
            receptive_field_size = tensor[0][0].numel()
        fan_in = num_input_fmaps * receptive_field_size
        fan_out = num_output_fmaps * receptive_field_size

    return fan_in, fan_out

计算fan_in和fan_out

　　　　　　关于gain的值选取，pytorch推荐如下：

　　　　也可以通过函数计算： gain = nn.init.calculate_gain("leaky_relu", 0.2) （ leaky_relu with negative_slope=0.2）

　　　　　　　　　　　　　　　 #第一个参数为nn.functional中的函数名，第二个为可选参树。

　　　　Kaiming/He Initialization：均值为0，标准差根据输入神经元的参数个数决定，特别采用适合ReLU激活函数的模型，详细见下面论文

　　　　论文：《Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification》

　　　　 nn.init.kaiming_uniform_(tensor, a=0, mode="fan_in", nonlinearity="leaky_relu"), 实现了（-bound, bound）范围内的均匀分布，计算公式如下：

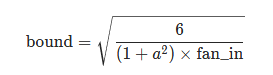
　　　　 nn.init.kaiming_normal_(tensor, a=0, mode="fan_in", nonlinearity="leaky_relu"): 实现了mean=0, std=std的正态分布，计算公式如下：

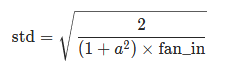
参数：
    tensor – n 维 torch.Tensor
    a – 该层后面一层的整流函数中负的斜率 (默认为 0，此时为 Relu)
    mode – ‘fan_in’ (default) 或者 ‘fan_out’。使用fan_in保持weights的方差在前向传播中不变；使用fan_out保持weights的方差在反向传播中不变。
    nonlinearity – 非线性函数 (nn.functional 中的名字)，推荐只使用 ‘relu’ 或 ‘leaky_relu’ (default)。

w = torch.empty(3, 3, 5, 5)          #fan_in=75, fan_out=75
nn.init.kaiming_uniform_(w, mode='fan_in', nonlinearity='relu')   #初始化为（-sqrt(6/75), sqrt(6/75)）范围内的均匀分布
nn.init.kaiming_normal_(w, mode='fan_out', nonlinearity='relu')    #初始化为mean=0, std=sqrt(2/75)的正态分布

　　1.3 初始化网络

　　　　在实际项目，要根据网络中的卷积核，BN和Linear等进行分开初始化，代码如下：

#coding:utf-8

import torch
import torch.nn as nn

class MyNet(nn.Module):
    
    def __init__(self):
        super(MyNet, self).__init__()
        self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1)  
        self.bn1 = nn.BatchNorm2d(64, eps=1e-05, momentum=0.1)
        self.relu1 = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(2, stride=2, padding=0)
        
        self.conv2 = nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1)   
        self.bn2 = nn.BatchNorm2d(128, eps=1e-05, momentum=0.1)
        self.relu2 = nn.ReLU(inplace=True)
        self.maxpool2 = nn.MaxPool2d(2, stride=2, padding=0)
        
        self.fc1 = nn.Linear(6 * 64 * 64, 150)
        self.relu3 = nn.ReLU(inplace=True)
        
        self.fc2 = nn.Linear(150, 3)
        self.softmax = nn.Softmax(dim=1)
        
    def froward(x):
        x = self.maxpool1(self.relu1(self.bn1(self.conv1(x))))
        x = self.maxpool2(self.relu2(self.bn2(self.conv2(x))))
        x = x.view(6 * 64 * 64, -1)
        x = self.relu3(self.fc1(x))
        x = self.softmax(self.fc1(x))
        return x

#初始化方法一        
def init_weights(net):
    for m in net.modules():
        if isinstance(m, nn.Conv2d):
            nn.init.kaiming_uniform_(m.weight, a=0, mode="fan_in", nonlinearity="relu")
            nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.BatchNorm2d):
            nn.init.constant_(m.weight, 1)
            nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.Linear):
            nn.init.normal_(m.weight, mean=0, std=1e-3)
            nn.init.constant_(m.bias, 0)
net = MyNet()
init_weights(net)
print(list(net.parameters())
    
#初始化方式二
def init_weights(m):
    if isinstance(m, nn.Conv2d):
        nn.init.xavier_uniform_(m.weight.data)
        nn.init.constant_(m.bias.data, 0.1)
    elif isinstance(m, nn.BatchNorm2d):
        m.weight.data.fill_(1)
        m.bias.data.zero_()
    elif isinstance(m, nn.Linear):
        m.weight.data.normal_(0, 0.01)
        m.bias.data.zero_()
net = MyNet()
net.apply(init_weights)
print(list(net.parameters()))

神经网络初始化

　　1.4 Xavier初始化和Kaiming初始化理论

　　　　xavier和kaiming初始化都是为了让最开始网络每层的输出均值为0，方差为1, 其理论推导比较复杂，想要深究的建议看下这几篇大佬的文章：

　　　　https://zhuanlan.zhihu.com/p/148034113

　　　　https://zhuanlan.zhihu.com/p/64464584

　　　　https://zhuanlan.zhihu.com/p/305055975

2. 优化器（optimizer）

　　神经网络训练时，采用梯度下降，更新权重参数，逐渐逼近最小loss的方式。pytorch中优化梯度下降的算法有多种，包括基于动量的SGD, SGD+Momentum, Nesterov, 和自适应的Adagrad, Adam.。

　　2.1 动量法

　　动量更新：动量法旨在通过每个参数在之前迭代中的梯度，来改变当前位置参数的梯度，在梯度稳定的地方能够加速更新的速度，在梯度不稳定的地方能够稳定梯度。

　　　2.1.1 SGD(stachastic gradient desent)

　　　随机梯度下降：最简单的梯度下降优化算法，每一个mini-batch 更新一次权重参数，公式如下， w为权重参数， $\frac{\partial L}{\partial W}$ 表示损失函数关于 $W$ 的梯度， $\eta$ 表示学习率。

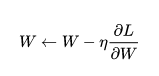
　　 SGD存在两个问题：

　　　　(1) SGD方法中的高方差振荡使得网络很难稳定收敛，即会之字形摇摆，收敛速度慢。

　　　　(2)可能会陷入局部最小值而无法跳出。

　　2.1.2 SGD+Momentum：加速训练，跳出局部最小值

　　　　　带动量的SGD优化器：在SGD的基础上引入动量，如下面公式中， $v$ 保存上一次的梯度， $\alpha$ 为衰减系数。可以发现每次梯度更新时，都会引入上一次的梯度值，如果本次梯度和上一次梯度方向相同，会加速梯度下降，而方向不一致时，能减小梯度下降，从而保证：梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛并减小震荡。

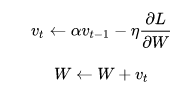
　　2.1.3 Nesterov: 也是一种动量更新的方式，不是很理解，更新公式如下，详细解释参见: https://zhuanlan.zhihu.com/p/151334819, https://zhuanlan.zhihu.com/p/22810533

　　　　 pytorch的optim.SGD()实现了上述三种优化算法：

　　　　　　optim.SGD(params, lr, momentum=0, dampening=0, weight_decay=0, nesterov=False)
　　　　　　　　params: 需要更新的权重参数,生成器对象
　　　　　　　　lr: 学习速率，常用0.001
　　　　　　　　momentum: 动量的权重系数，对应上面式子中的 $\alpha$ ，默认为0，表示不采用动量更新。常用0.8和0.9
　　　　　　　　nesterov: 是否采用Nesterov动量更新方式
　　　　　　　　weight_decay: L2正则惩罚项的系数, 默认为0表示不进行正则化惩罚。常用1e-5

from torch import optim
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)  #model.parameters()， 神经网络的权重参数

　　2.2 自适应法　

　　　　自适应更新：它通过每个参数的历史梯度，动态更新每一个参数的学习率，使得每个参数的更新率都能够逐渐减小。前期梯度加大的，学习率减小得更快，梯度小的，学习率减小得更慢些。（能解决 SGD 遇到鞍点或者极小值点后学习变慢的问题）

　　　2.2.1 Adagrad：自适应的调节学习率，更新算法如下，h中储存了梯度的平方值，梯度越大时，h越大，而学习率会越小。

　　　　optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0)

d = (torch.randn(5, 3) for i in range(3))
optimizer = optim.Adagrad(d, lr=0.001)
print(optimizer)

　　2.2.2 RMSprop （Root mean square）: Adagrad有个问题，其学习率会不断地衰退，会使得很多任务在达到最优解之前学习率就已经过量减小，所以RMSprop采用了使用指数衰减平均来慢慢丢弃先前得梯度历史，防止学习率过早地减小。其更新公式如下：

　　　　optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)

　　　　　　alpha: 对应上式子中的ρ，默认为0.99

　　　　　　eps: 为数学稳定项，对应上式子中的δ，默认为1e-08

params = (torch.randn(5, 3) for i in range(3))
optimizer = optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
print(optimizer)

　　AdaDelta

from mxnet import gluon, optimizer
optim = optimizer.AdaDelta(rho=0.9)
trainer = gluon.Trainer(net.collect_params(), optimizer="adadelta", optimizer_params={"rho": 0.9})

　　2.2.3 Adam：结合了上述的动量（Momentum）和自适应（Adaptive），同时对梯度和学习率进行动态调整。如果说动量相当于给优化过程增加了惯性，那么自适应过程就像是给优化过程加入了阻力。速度越快，阻力也会越大。更新公式如下：

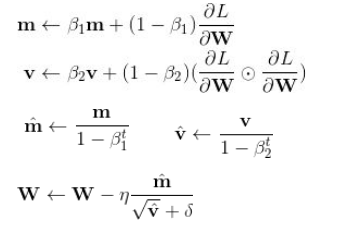
　　optim.Adam(params, lr=0.001, beats=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)

　　　　betas: 对应上述式子中的β1，β2，默认β1=0.9， β2=0.999

params = (torch.randn(5, 3) for i in range(3))
optimizer = optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=Fals)
print(optimizer)

　　2.3 优化器使用

　　　　上述几种优化器，对params中的参数全部使用相同的学习速率，在实际训练模型时，也可以为模型不同层设置不同的学习速率。代码如下：

　　　　使用相同的学习速率：

#coding:utf-8

import torch
import torch.nn as nn
from torch import optim

class MyNet(nn.Module):
    
    def __init__(self):
        super(MyNet, self).__init__()
        self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1)  
        self.bn1 = nn.BatchNorm2d(64, eps=1e-05, momentum=0.1)
        self.relu1 = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(2, stride=2, padding=0)
        
        self.conv2 = nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1)   
        self.bn2 = nn.BatchNorm2d(128, eps=1e-05, momentum=0.1)
        self.relu2 = nn.ReLU(inplace=True)
        self.maxpool2 = nn.MaxPool2d(2, stride=2, padding=0)
        
        self.fc1 = nn.Linear(6 * 64 * 64, 150)
        self.relu3 = nn.ReLU(inplace=True)
        
        self.fc2 = nn.Linear(150, 3)
        self.softmax = nn.Softmax(dim=1)
        
    def froward(x):
        x = self.maxpool1(self.relu1(self.bn1(self.conv1(x))))
        x = self.maxpool2(self.relu2(self.bn2(self.conv2(x))))
        x = x.view(6 * 64 * 64, -1)
        x = self.relu3(self.fc1(x))
        x = self.softmax(self.fc1(x))
        return x
        
model = MyNet()
optimizer = optim.Adam(model.parameters(), lr=0.001, weight_decay=1e-05)
print(optimizer)

#dataset得自己实现
for input, target in dataset:
    optimizer.zero_grad()
    output = model(input)
    loss = loss_fn(output, target)
    loss.backward()
    optimizer.step()

模型中optimizer

　　　　使用不同的学习速率：

#coding:utf-8

import torch
import torch.nn as nn
from torch import optim

class MyNet(nn.Module):
    
    def __init__(self):
        super(MyNet, self).__init__()
        self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1)  
        self.bn1 = nn.BatchNorm2d(64, eps=1e-05, momentum=0.1)
        self.relu1 = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(2, stride=2, padding=0)
        
        self.conv2 = nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1)   
        self.bn2 = nn.BatchNorm2d(128, eps=1e-05, momentum=0.1)
        self.relu2 = nn.ReLU(inplace=True)
        self.maxpool2 = nn.MaxPool2d(2, stride=2, padding=0)
        
        self.fc1 = nn.Linear(6 * 64 * 64, 150)
        self.relu3 = nn.ReLU(inplace=True)
        
        self.fc2 = nn.Linear(150, 3)
        self.softmax = nn.Softmax(dim=1)
        
    def froward(x):
        x = self.maxpool1(self.relu1(self.bn1(self.conv1(x))))
        x = self.maxpool2(self.relu2(self.bn2(self.conv2(x))))
        x = x.view(6 * 64 * 64, -1)
        x = self.relu3(self.fc1(x))
        x = self.softmax(self.fc1(x))
        return x
        
model = MyNet()

conv1_params = list(map(id, model.conv1.parameters()))
conv2_params = list(map(id, model.conv2.parameters()))
base_params = filter(lambda p: id(p) not in conv1_params+conv2_params, model.parameters())
params = [{"params": base_params},
          {"params": model.conv1.parameters(), "lr": 0.001, "weight_decay":1e-05},
          {"params": model.conv2.parameters(), "lr": 0.001, "weight_decay":1e-05}
]
optimizer = optim.Adam(params, lr=0.01, weight_decay=1e-04)  #base_params采用lr=0.01, weight_decay=1e-04； conv1和conv2层采用单独的学习速率
print(optimizer)


#dataset得自己实现
for input, target in dataset:
    optimizer.zero_grad()
    output = model(input)
    loss = loss_fn(output, target)
    loss.backward()
    optimizer.step()

模型中optimizer

3. 图片预处理

　　在进行训练模型前，有时候会对图片进行预处理，主要包括两方面： PCA降维和图片增强

　　3.1 PCA降维

　　　　提取图片的主要特征，同时能对一些较大的图片进行压缩。原理推导过程如下：（参考1，参考2）

　　　　数学原理参考：http://blog.codinglabs.org/articles/pca-tutorial.html

PCA算法步骤

　　(1)将数据组织成d =m*n(特征为n维，每个维度上有每个数据)的矩阵，减去每一个维度上的均值（若不同维度间的数据尺度相差大时，还需除以标准差）

　　(2)计算矩阵d的协方差矩阵（dT *d）

　　(3)对协方差矩阵进行特征分解（或奇异值分解）

　　(4) 选取较大特征值对应的特征向量作为基向量，将矩阵的映射到基向量空间，即完成降维

使用代码如下：

#coding:utf-8


import numpy as np


#对x进行PCA将维
x = np.random.randn(1000, 500)
x -= np.mean(x, axis=0)
cov = np.dot(x.T, x)/(x.shape[0] -1)  #x的协方差矩阵
u, s, v = np.linalg.svd(cov)  #奇异值分解
x_reduced = np.dot(x, u[:, :100])  #取前100个特征向量（根据特征值大小从到小排列）

PCA降维

#coding:utf-8


import numpy as np
from sklearn.decomposition import PCA 
import cv2


def my_pca(x, n=100):
    #对x进行PCA将维
    x = x-np.mean(x, axis=0)
    cov = np.dot(x.T, x)/(x.shape[0] -1)  #x的协方差矩阵, (n-1：除以n-1表示是样本方差; 若是所有样本的方差则除以n；参见https://www.cnblogs.com/datamining-bio/p/9267759.html)
    # cov = np.cov(x, rowvar=0)  #计算协方差矩阵，注意此处rowvar=0表示，一列数据表示一个特征/一个维度
    u, s, v = np.linalg.svd(cov)  #奇异值分解
    x_reduced = np.dot(x, u[:, :n])  #取前100个特征向量（根据特征值大小从到小排列）
    return x_reduced
    
def my_pca2(x, n=100):
    #对x进行PCA将维
    x = x-np.mean(x, axis=0)
    cov = np.dot(x.T, x)/(x.shape[0] -1)  #x的协方差矩阵, (n-1：除以n-1表示是样本方差; 若是所有样本的方差则除以n；参见https://www.cnblogs.com/datamining-bio/p/9267759.html)
    #cov = np.cov(x, rowvar=0)  #计算协方差矩阵，注意此处rowvar=0表示，一列数据表示一个特征/一个维度
    eig_values, eig_vector = np.linalg.eig(cov)   #特征值分解
    index = np.argsort(-eig_values)[:n]     #按特征值排序，挑选出特征值最大的100个特征值index，随后取出其对应的100个特征向量
    x_reduced = np.dot(x, eig_vector[:, :n])  #取前100个特征向量（根据特征值大小从到小排列）
    return x_reduced

if __name__ == "__main__":
    data = np.random.randn(1000, 500)   #表示1000条数据，一条数据有500个特征
    r1 = my_pca(data)
    r2= my_pca2(data)
    

    pca=PCA(n_components=100)     #加载PCA算法，设置降维后主成分数目为2
    reduced_x=pca.fit_transform(data)#对样本进行降维
    
    #三种方法计算出来的降维数据并不近似相等，不是很理解？？
    print(np.allclose(r1, reduced_x, equal_nan=True))   #False
    print(np.allclose(r2, reduced_x,  equal_nan=True))  #False
    print(np.allclose(r2, r1, equal_nan=True))          #False

降维方法对比

　　　3.2 图片增强

　　　　对图片进行旋转，颜色转换，投影变换等来增强图片的多样性，减少模型训练过拟合，使模型更加鲁棒，简单代码如下：

#!/usr/bin/env python
#coding:utf-8



import cv2 as cv
import numpy as np
import random
import argparse
import os

def crop(img,roi):
    """
    img: 图像矩阵
    roi: 待截取的区域，格式为：(top,bottom,left,right)
    """
    top,bottom,left,right=roi
    bottom = img.shape[0] if bottom>img.shape[0] else bottom
    right = img.shape[1] if right>img.shape[1] else right
    return img[top:bottom,left:right]
    
def color_shift(img,shift=50):
    """
    img: 图像矩阵
    shift: 像素值偏移值
    """
    r_offset = random.randint(-abs(shift),abs(shift))
    g_offset = random.randint(-abs(shift),abs(shift))
    b_offset = random.randint(-abs(shift),abs(shift))
    img = img+np.array([b_offset,g_offset,r_offset])
    img[img<0]=0
    img[img>255]=255
    return img
    
def rotate(img,angle=30,scale=1):
    """
    img: 图像矩阵
    angle: 选转角度
    scale:缩放因子
    """
    rows,cols = img.shape[:2]
    M = cv.getRotationMatrix2D((int(cols/2),int(rows/2)),angle,scale)
    img_rotate = cv.warpAffine(img,M,(cols,rows))
    return img_rotate
def perspective(img,random_margin=60):
    """
    img: 图像矩阵
    random_margin: 随机值，用来生成坐标
    """
    height,width = img.shape[:2]
    x1 = random.randint(-random_margin, random_margin)
    y1 = random.randint(-random_margin, random_margin)
    x2 = random.randint(width - random_margin - 1, width - 1)
    y2 = random.randint(-random_margin, random_margin)
    x3 = random.randint(width - random_margin - 1, width - 1)
    y3 = random.randint(height - random_margin - 1, height - 1)
    x4 = random.randint(-random_margin, random_margin)
    y4 = random.randint(height - random_margin - 1, height - 1)

    dx1 = random.randint(-random_margin, random_margin)
    dy1 = random.randint(-random_margin, random_margin)
    dx2 = random.randint(width - random_margin - 1, width - 1)
    dy2 = random.randint(-random_margin, random_margin)
    dx3 = random.randint(width - random_margin - 1, width - 1)
    dy3 = random.randint(height - random_margin - 1, height - 1)
    dx4 = random.randint(-random_margin, random_margin)
    dy4 = random.randint(height - random_margin - 1, height - 1)

    pts1 = np.float32([[x1, y1], [x2, y2], [x3, y3], [x4, y4]])
    pts2 = np.float32([[dx1, dy1], [dx2, dy2], [dx3, dy3], [dx4, dy4]])
    M = cv.getPerspectiveTransform(pts1,pts2)
    img_pers = cv.warpPerspective(img,M,(width,height))
    return img_pers

# def perspective(img,pos1,pos2):
    # """
    # img: 图像矩阵
    # pos1: 原图像中四组坐标值, 格式为((x1,y1),(x2,y2),(x3,y3),(x4,y4))
    # pos2 投影变换后图像中四组坐标值,格式同from
    # """
    # pos1 = np.float32(pos1)
    # pos2 = np.float32(pos2)
    # M = cv.getPerspectiveTransform(pos1,pos2)
    # img_pers = cv.warpPerspective(img,M,(img.shape[1],img.shape[0]))
    # return img_pers

def argparser():
    parser = argparse.ArgumentParser()
    parser.add_argument("--img_input", type=str,help="输入图片路径")
    parser.add_argument("--img_output", type=str,help="输出图片路径")
    parser.add_argument("--roi", nargs='*',type=int,help="待截取的区域，格式为：(top,bottom,left,right)")
    parser.add_argument("--shift",type=int,help="像素值偏移值")
    parser.add_argument("--angle",type=float,help="旋转角度")
    parser.add_argument("--scale",type=float,help="缩放因子")
    parser.add_argument("--margin",type=int,help="随机值，用来生成坐标")
    
    return parser.parse_args()

if __name__=="__main__":
    parse = argparser()
    img_dir = parse.img_input
    out_dir = parse.img_output
    if not os.path.exists(out_dir):
        os.makedirs(out_dir)
    if os.path.exists(img_dir):
        for file in os.listdir(img_dir):
            if file.endswith(("jpg","png")):
                img = cv.imread(os.path.join(img_dir,file))
                if parse.roi and len(parse.roi)==4:
                    img = crop(img,parse.roi)
                if parse.shift:
                    img = color_shift(img,parse.shift)
                if parse.angle and parse.scale:
                    img = rotate(img,parse.angle,parse.scale)
                if parse.margin:
                    img = perspective(img,parse.margin)
                cv.imwrite(os.path.join(out_dir,file),img)

图像增强

gluoncv的SSD算法中对图片的增强处理，包括brightness，contrast，hue，saturation的处理，源码如下：

"""Experimental image transformations."""
from __future__ import division
import random
import numpy as np
import mxnet as mx
from mxnet import nd

def random_color_distort(src, brightness_delta=32, contrast_low=0.5, contrast_high=1.5,
                         saturation_low=0.5, saturation_high=1.5, hue_delta=18):
    """Randomly distort image color space.
    Note that input image should in original range [0, 255].

    Parameters
    ----------
    src : mxnet.nd.NDArray
        Input image as HWC format.
    brightness_delta : int
        Maximum brightness delta. Defaults to 32.
    contrast_low : float
        Lowest contrast. Defaults to 0.5.
    contrast_high : float
        Highest contrast. Defaults to 1.5.
    saturation_low : float
        Lowest saturation. Defaults to 0.5.
    saturation_high : float
        Highest saturation. Defaults to 1.5.
    hue_delta : int
        Maximum hue delta. Defaults to 18.

    Returns
    -------
    mxnet.nd.NDArray
        Distorted image in HWC format.

    """
    def brightness(src, delta, p=0.5):
        """Brightness distortion."""
        if np.random.uniform(0, 1) > p:
            delta = np.random.uniform(-delta, delta)
            src += delta
            return src
        return src

    def contrast(src, low, high, p=0.5):
        """Contrast distortion"""
        if np.random.uniform(0, 1) > p:
            alpha = np.random.uniform(low, high)
            src *= alpha
            return src
        return src

    def saturation(src, low, high, p=0.5):
        """Saturation distortion."""
        if np.random.uniform(0, 1) > p:
            alpha = np.random.uniform(low, high)
            gray = src * nd.array([[[0.299, 0.587, 0.114]]], ctx=src.context)
            gray = mx.nd.sum(gray, axis=2, keepdims=True)
            gray *= (1.0 - alpha)
            src *= alpha
            src += gray
            return src
        return src

    def hue(src, delta, p=0.5):
        """Hue distortion"""
        if np.random.uniform(0, 1) > p:
            alpha = random.uniform(-delta, delta)
            u = np.cos(alpha * np.pi)
            w = np.sin(alpha * np.pi)
            bt = np.array([[1.0, 0.0, 0.0],
                           [0.0, u, -w],
                           [0.0, w, u]])
            tyiq = np.array([[0.299, 0.587, 0.114],
                             [0.596, -0.274, -0.321],
                             [0.211, -0.523, 0.311]])
            ityiq = np.array([[1.0, 0.956, 0.621],
                              [1.0, -0.272, -0.647],
                              [1.0, -1.107, 1.705]])
            t = np.dot(np.dot(ityiq, bt), tyiq).T
            src = nd.dot(src, nd.array(t, ctx=src.context))
            return src
        return src

    src = src.astype('float32')

    # brightness
    src = brightness(src, brightness_delta)

    # color jitter
    if np.random.randint(0, 2):
        src = contrast(src, contrast_low, contrast_high)
        src = saturation(src, saturation_low, saturation_high)
        src = hue(src, hue_delta)
    else:
        src = saturation(src, saturation_low, saturation_high)
        src = hue(src, hue_delta)
        src = contrast(src, contrast_low, contrast_high)
    return src

SSD color Transform

参考：https://www.jianshu.com/p/03009cfdf733

　　 https://zhuanlan.zhihu.com/p/39076763

https://zhuanlan.zhihu.com/p/79981927

　　 https://segmentfault.com/a/1190000012668819?utm_source=tag-newest

posted @ 2019-10-02 21:53 silence_cho 阅读(2672) 评论(0) 编辑收藏举报

刷新页面返回顶部

silence_cho

pytorch基础学习（二）

公告