查找与排序算法（Searching adn Sorting）

1，查找算法

　　常用的查找算法包括顺序查找，二分查找和哈希查找。

　　1.1 顺序查找(Sequential search)

　　　　顺序查找： 依次遍历列表中每一个元素，查看是否为目标元素。python实现代码如下：　　

#无序列表
def sequentialSearch(alist,item):
    found = False
    pos=0
    while not found and pos<len(alist):
        if alist[pos]==item:
            found=True
        else:
            pos = pos+1
    return found
testlist = [1, 2, 32, 8, 17, 19, 42, 13, 0]
print(sequentialSearch(testlist, 3))
print(sequentialSearch(testlist, 13))

#有序列表(升序)
def orderedSequentialSearch(orderedList,item):
    found = False
    pos = 0
    stop = False
    while not found and not stop and pos<len(orderedList):
        if orderedList[pos]==item:
            found=True
        else:
            if orderedList[pos]>item:
                stop=True
            else:
                pos = pos+1
    return found
testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(orderedSequentialSearch(testlist, 3))
print(orderedSequentialSearch(testlist, 13))

　　　　顺序查找的复杂度分析如下，无论对于有序列表或无序列表，在最差的情况下，其都需要进行n次比较运算，所以其复杂度为O(n)

　　　　查找无序列表：

　　　　　　

　　　　查找有序列表：（仅仅在item不存在时，性能有所提高）

　　　　　　

　　1.2 二分查找（Binary search）

　　　　二分查找：二分查找又叫折半查找，适用于有序列表。查找的方法是找到列表正中间的值，我们假设是m，来跟v相比，如果m>v，说明我们要查找的v在前列表的前半部，否则就在后半部。无论是在前半部还是后半部，将那部分再次折半查找，重复这个过程，知道查找到v值所在的地方。实现二分查找可以用循环，也可以递归。

　　　　下图为查找54的过程：

　　　　

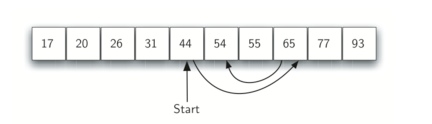
　　　　使用循环，python实现代码如下：

#循环
def binarySearch(orderedList,item):
    found =False
    first = 0
    last = len(orderedList)-1
    while not found and first<=last:
        midpoint = (first+last)//2
        if orderedList[midpoint]==item:
            found=True
        elif orderedList[midpoint]>item:
            last = midpoint-1
        else:
            first = midpoint+1
    return found
testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearch(testlist, 3))
print(binarySearch(testlist, 13))

　　　　使用递归，python实现代码如下：

#递归
def binarySearch(orderedList,item):
    if len(orderedList)==0:
        return False
    else:
        midpoint = len(orderedList) // 2
        if orderedList[midpoint] == item:
            return True
        elif orderedList[midpoint] > item:
            return binarySearch(orderedList[:midpoint],item)  #注意得return
        else:
            return binarySearch(orderedList[midpoint+1:], item)  #注意得return
testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearch(testlist, 3))
print(binarySearch(testlist, 17))

　　二分查找的时间复杂度分析：最好情况下为1，最坏情况下为log n，因此复杂度为O(log n)。但值得注意的是，使用递归时，进行列表的切片的复杂度为O(K)，并不是依次操作，所以复杂度变大。（可以将切片改为传入索引值： return binarySearch(orderedList,0,midpoint-1,item)和return binarySearch(orderedList,midpoint+1,len(orderedList),item)）

　　1.3 哈希查找（Hash Search）

　　哈希技术（Hashing）:哈希技术是在数据的存储位置和数据的 key 之间建立一个确定的映射 f()，使得每个 key 对应一个存储位置 f(key)，其中f()称作哈希函数（hash function），记录数据存储位置的数据结构为哈希表（hash table）.如下图中为一个空的哈希表，key从0-10，共有11个存储位置。

　　　　

　　　为存储数据54, 26, 93, 17, 77, and 31，以除留余数法（remainder method）为哈希函数: f(n)=n%11，依次计算对应哈希值，如下表所示：

　　　　　　

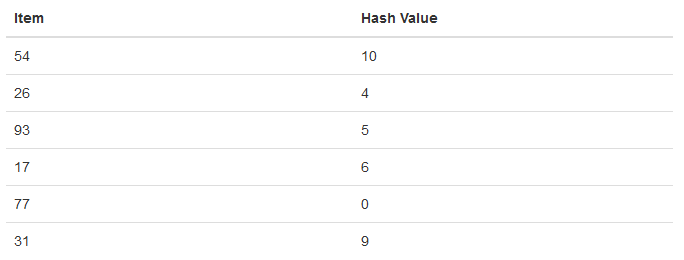
　　根据计算的hash value，以其为哈希表的key，依次将数据存储在哈希表中，结果如下图所示，当我们需要查找31时，只需利用哈希函数就能找到该数据的存储位置，比较值便能确定是否包含该数据，算符复杂度能达到O(1).

　   　

 　　哈希函数进行映射时，会出现两个问题，一是部分存储位置会空缺，造成哈希表的浪费；二是会出现碰撞，如存储44到上述哈希表中，会和77所在的存储位置碰撞。因此，需要有效的哈希函数和碰撞解决途径

　　1.3.1 其他哈希函数

　　　　折叠法（folding method）:

　　　　　　如对于电话号码436-555-4601，对其拆分求和 43+65+55+46+01=210，再以哈希表的长度求余数（210%11=1）

　　　　　　对于字符串‘cat’，将其转换为Ascill表中数值99,97,116，进行求和，再以哈希表的长度求余数。

　　　　平方取中法（mid-square method）:

　　　　　　如对于数据44，对其进行平方44*44=1936，取中间两位93，再以哈希表的长度求余数（93%11=5）

　　1.3.2 冲突解决途径(collision resolution):

　　　　（为了更好的解决冲突，哈希表的长度应该为质数）

　　　　开放定址法（open addressing）:

　　　　　　该方法是一旦发生冲突，求从哈希表的当前位置依次往后寻找下一个空的存储位置，然后将其插入。。

　　　　　　二次探测(rehashing):上面方法会造成多个哈希值集中在某一区域，争夺同一个地址。可以利用哈希值加上一个数值，再以哈希表的长度求余数。

　　　　　　　　　　随机探测：哈希值加上一个随机数（1,3...）。

　　　　　　　　　　　　　　　　如上面提到的44插入哈希表时哈希值为0，会和77的哈希值冲突，可以哈希值加一个随机数3，重新计算（0+3）%11=3，

　　　　　　　　　　　　　　　　由于3号位置空缺，因此将44插入。（若依旧冲突，继续加3）

　　　　　　　　　　平方探测：哈希值加上一个平方数（1,4,9,16）。第一次冲突加1，继续冲突时加4，还是冲突时加9，如此重复下去直到找到数据

　　　　链地址法(chain addressing)：发生冲突的数据依次放在一个链表中，哈希表中存放链表地址，如下图所示:

　　　　　　　　　　　　　　

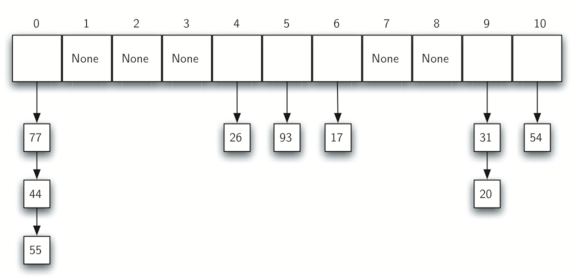
　　1.3.3 字典的实现（Map）

　　　　python的字典就是一种Map数据结构，利用哈希算法来实现键值对的储存和查找。

　　　　map常用操作如下：

Map()   #创建字典
put(key,value)    #加入键值对
get(key)     #返回对应value
len()    # 返回字典长度
del     #删除字典键值对
in     #查找是否包含键

　　　　利用python 实现代码如下：（del如何实现？）

class Map(object):
    def __init__(self):
        self.size = 11   #哈希表的长度
        self.slots=[None]*self.size     #存放key
        self.data = [None]*self.size    #存放value
    def put(self,key,value):
        hashvalue = self._hashfunction(key,len(self.slots))
        if self.slots[hashvalue]==None:
            self.slots[hashvalue]=key
            self.data[hashvalue]=value
        else:
            if self.slots[hashvalue]==key:
                self.data[hashvalue]=value
            else:
                nextslot = self._rehash(hashvalue,len(self.slots))
                while self.slots[nextslot]!=None and self.slots[nextslot]!=key:  #如果某个键值对删除了，会不会出现key之前有None？
                    nextslot = self._rehash(nextslot,len(self.slots))

                if self.slots[nextslot] == None:
                    self.slots[nextslot] = key
                    self.data[nextslot] = value
                else:
                    self.data[nextslot] = value
#del 如何实现？
    def _hashfunction(self,key,size):
        return key%size

    def _rehash(self,oldhash,size):
        return (oldhash+1)%size

    def get(self,key):
        startslot = self._hashfunction(key,len(self.slots))
        found = False
        stop = False
        data = None
        position = startslot
        while self.slots[position]!=None and not found and not stop:
            if self.slots[position]==key:
                data = self.data[position]
                found = True
            else:
                position = self._rehash(position,len(self.slots))
                if position==startslot:
                    stop=True
        return data

    def __setitem__(self, key, value):
        self.put(key,value)

    def __getitem__(self, item):
        return self.get(item)

m = Map()
m[54] = 'cat'
m[26] = 'dog'
m[12] = 'snake'
m[52] = 'bear'
m[93]="lion"
m[17]="tiger"
m[77]="bird"
m[31]="cow"
m[44]="goat"
m[55]="pig"
m[20]="chicken"
print m.slots,m.data
# print m[12],m[20]
#删除m[77]会引起bug？ 
# m.slots[0]=None
m[44]= "not goat"
print m.slots,m.data

　　　　由于冲突存在，哈希查找的复杂度并不完全是O(1)，取决于哈希表的负载因子（load factor）λ，λ=(numbers of key)/tablesize，即哈希表中key的数量。

　　　　λ越大时，表明key越多，发生碰撞的可能性越高，查找会变慢，λ越小时，碰撞可能性小，但空间资源浪费多。（python中字典的默认拉姆达为0.75？）

　　　　采用开放定址中随机探测解决冲突，平均复杂度为 (1+1/(1-r))/2，最坏情况为(1+1/(1-r)²)/2

　　　　采用链地址法解决冲突，平均复杂度为 1+λ/2，最坏情况为λ

2，排序算法

　　常用的排序算法包括：冒泡排序(Bubble sort)，选择排序(Selection sort)，插入排序(Insertion sort)，希尔排序(Shell sort)，归并排序(Merge sort)和快速排序(Quick sort)

　　2.1 冒泡排序（Bubble sort）

　　　　冒泡排序：依次比较相邻的两个数，将小数放在前面，大数放在后面。

　　　    排序过程：在第一趟：首先比较第1个和第2个数，将小数放前，大数放后。然后比较第2个数和第3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后，第一趟排序完成后最大的数被移动到了最后面。继续重复第一趟步骤，直至全部排序完成。下图为第一趟排序过程：

　　　　　　　　　　　　　　　　　　

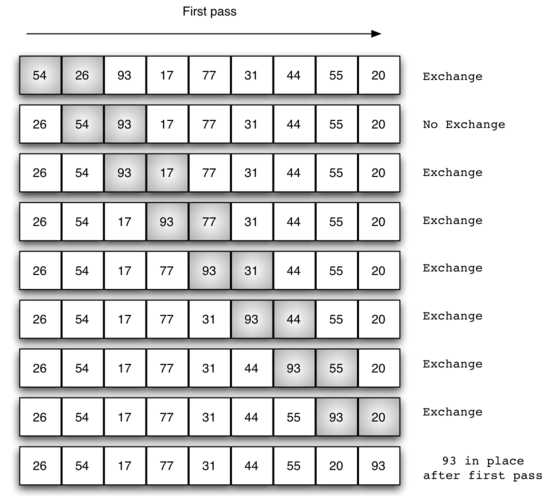
　　　　用python实现代码如下：

def bubbleSort(alist):
    for n in range(len(alist)-1,0,-1):
        for i in range(n):
            if alist[i]>alist[i+1]:
                alist[i],alist[i+1]=alist[i+1],alist[i]
alist = [54,26,93,17,77,31,44,55,20]
bubbleSort(alist)
print(alist)

　　　　无论列表是否有序，冒泡算法都需要进行比较，共需要进行n*(n-1)/2 次比较，最好的情况下，列表有序时不需要交换，最坏的情况下需要n*(n-1)/2 次交换（每次比较都进行交换），因此冒泡排序的复杂度为O(n²)。对于冒泡排序可以进行改进，使其在列表有序时能停止比较，即短冒泡排序（short bubble），代码如下：

def shortBubbleSort(alist):
    n = len(alist)-1
    exchange = True
    while n>0 and exchange:
        exchange = False
        for i in range(n):
            if alist[i]>alist[i+1]:
                exchange = True
                alist[i],alist[i+1]=alist[i+1],alist[i]
        n = n-1
alist=[20,30,40,90,50,60,70,80,100,110]
shortBubbleSort(alist)
print(alist)

　　　　2.2 选择排序（selection sort）

　　　　　　选择排序：每一趟从待排序的记录中选出最大的元素，放在已排好序的序列最后，直到全部记录排序完毕。（相比冒泡排序，选择排序每一趟只进行一次交换）

　　　　　　　　　　排序过程如下图(前四趟)：

　　　　　　　　　　　　　　　　　　

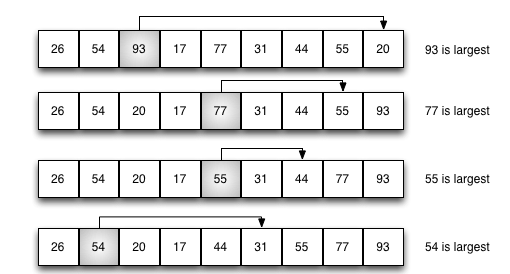
　　　　　　用python实现代码如下：

def selectionSort(alist):
    for n in range(len(alist)-1,0,-1):
        pos = n
        for i in range(n):
            if alist[i]>alist[pos]:
                pos = i
        alist[n],alist[pos]=alist[pos],alist[n]

alist = [54,26,93,107,77,31,44,55,28]
selectionSort(alist)
print(alist)

　　　　　　选择排序和冒泡一样，也需要进行n*(n-1)/2 次比较，但交换列表中数据次数减少，最坏情况下需要n-1次交换，所以复杂度也为O(n²)。

　　　　2.3 插入排序（Insertion sort）

　　　　　　插入排序：已排序部分定义在左端，将未排序部分元的第一个元素插入到已排序部分合适的位置。排序过程示意如下：

　　　　　　　　　　　　

　　　　　　　　用python实现代码如下：（插入到有序序列时也可以考虑二分查找）

def insertionSort(alist):

    for i in range(1,len(alist)):
        pos = i
        currentvalue = alist[i]
        while alist[pos-1]>currentvalue and pos>0:
            alist[pos]=alist[pos-1]
            pos = pos-1
        alist[pos]=currentvalue

alist = [54,26,93,17,77,31,44,55,20]
insertionSort(alist)

　　　　　　　　插入排序的复杂度为为O(n²)，其在最好的情况下（列表有序），复杂度为n，最坏的情况下，复杂度为n*(n-1)/2

　　　　2.4 希尔排序（Shell sort）

　　　　　　希尔排序：增量递减排序（diminishing increment sort），是对插入排序的改进，减少数据移动操作。其主要是引入一个增量（gap），将原本的序列分成几个子序列，分别对子序列采用插入排序。排序示意过程如下：

　　　　　　1,先以3为增量，将序列分为了三个子序列（54,17,44），（26,77，55），（93, 31, 20），分别对三个子序列进行插入排序

　　　　　　　　         

 

　　　　　　2，再以1为增量（即整个序列），然后再用插入排序，如下图所示，可以发现shift操作明显减少

　　　　　　　　　　

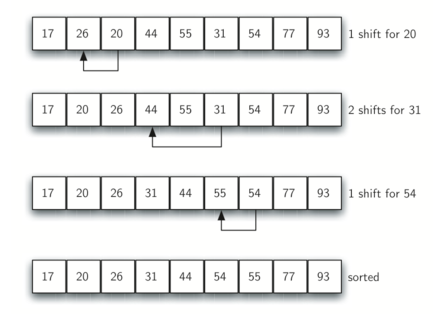
　　　　对于希尔排序，增量的选择十分重要，上面选择了增量3，1。一般也可以选择将增量n/2，n/4....,1(n为列表长度)，上面序列若选择4（n/2）为初始增量，子序列如下：

　　　　　　　　　　　　

 

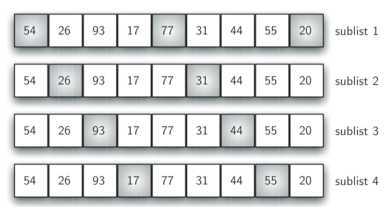
　　　　python实现希尔排序代码如下：（增量为n/2，n/4....,1）

def shellSort(alist):
    gap = len(alist)//2
    while gap>0 :
        for i in range(gap):
            gapInsertionSort(i,alist,gap)
        #print "增量为%s,排序完成后alist为: %s"%(gap,alist)
        gap = gap//2
def gapInsertionSort(startPos,alist,gap):
    for i in range(startPos+gap,len(alist),gap):
        current = alist[i]
        pos = i
        while alist[pos-gap]>current and pos>=gap:
            alist[pos] = alist[pos-gap]
            pos = pos-gap
        alist[pos] = current
alist = [54,26,93,17,77,31,44,55,20]
shellSort(alist)
print alist

　　　　希尔排序的复杂度在O(n)—O(n²)之间，对于上面的gap（n/2,n/4..1）复杂度为O(n²)，若gap为2k-1(1,3,5,7...)，复杂度为O(n^3/2)

 　　　　2.5 归并排序（Merge sort）

　　　　　　　归并排序：是一种分而治之的策略（divide and conquer）。采用递归算法，不断的将序列进平分成子序列，直到序列为空或只有一个元素，然后进行排序合并。其排序过程如下：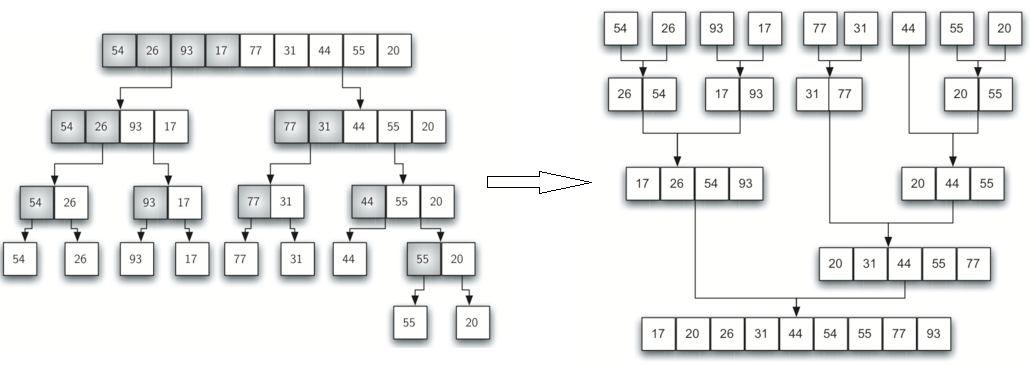

　　　　python实现归并排序代码如下：

def mergeSort(alist):
    #print "平分序列，alist:%s"%alist
    if len(alist)>1:
        mid = len(alist)//2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]
        mergeSort(lefthalf)
        mergeSort(righthalf)

        i=0
        j=0
        k=0
        while i<len(lefthalf) and j<len(righthalf):
            if lefthalf[i]>righthalf[j]:
                alist[k]=righthalf[j]
                j+=1
            else:
                alist[k]=lefthalf[i]
                i+=1
            k+=1

        while i<len(lefthalf):
            alist[k]=lefthalf[i]
            i+=1
            k+=1

        while j<len(righthalf):
            alist[k]=righthalf[j]
            j+=1
            k+=1

    #print "开始合并,alist: %s"%alist

alist = [54,26,93,17,77,31,44,55,20]
mergeSort(alist)
print alist

　　　　归并排序的复杂度为O(n logn)，但上述代码中使用了切片，会使复杂度增加。（切片可以改为传入index？）

　　　　2.6 快速排序（quick sort）

　　　　　　快速排序：也是一种分而治之的策略（divide and conquer）。但相比归并排序，快速排序不需要额外的存储空间（列表）。快速排序一般选择列表中一个元素中间点（pivot value），然后将比其小的元素放在列表左边，大的放在右边，将列表进行划分为左右两个子列表，再分别对左右子列表递归的快速排序。排序过程如下（选取第一个元素为中间点）：

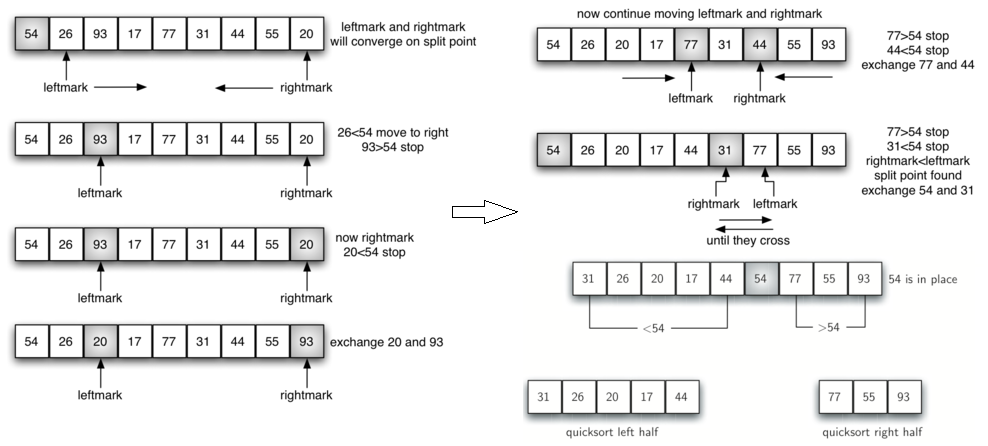
　　　　python实现快速排序代码如下：

def quickSort(alist):
    quickSortHelper(alist,0,len(alist)-1)

def quickSortHelper(alist,first,last):
    if first<last:
        pivotvalue = alist[first]
        leftmark = first+1
        rightmark = last
        done = False
        while not done:
            while  leftmark<=rightmark and alist[leftmark]<=pivotvalue: #注意两个判断条件的前后顺序不能换，否则leftmark=last-1时可能会报错：list index out of range
                leftmark = leftmark+1
            while alist[rightmark]>=pivotvalue and leftmark<=rightmark:
                rightmark = rightmark-1
            if leftmark<rightmark:
                alist[leftmark],alist[rightmark]=alist[rightmark],alist[leftmark]
            else:
                done = True
        alist[first],alist[rightmark]=alist[rightmark],alist[first]
        print alist
        quickSortHelper(alist,first,rightmark-1)
        quickSortHelper(alist,rightmark+1,last)

alist = [54,26,93,17,98,77,31,44,55,20]
quickSort(alist)
print alist

def quick_sort(alist):
    if len(alist)<2:
        return alist
    else:
        midpivot = alist[0]
        less_than_mid = [i for i in alist[1:] if i<=midpivot]
        greater_than_mid = [i for i in alist[1:] if i>midpivot]
        final_list = quick_sort(less_than_mid)+[midpivot]+quick_sort(greater_than_mid)
        return final_list
alist = [2,4,6,7,1,2,5]
print(quick_sort(alist))

　　　

             快速排序的复杂度取决于pivot value的选择，如果每次分割都为序列中间值，则需logn分割，复杂度为O(n logn)，若每次分割pivot value都为最小或最大值，则需n次分割，复杂度为O(n²)，复杂度没有归并排序稳定，但不需要额外的内存。 因此选择pivot value值时，可以从序列的first, middle, last三个元素中选择中间值（median of three），来避免总是选择最小或最大值

　　　为了避免快速排序复杂度变为O(n²)，可以对pivot value的选取进行优化：主要是基于随机值和三路快排

　　　简单快速排序：总是选取列表第一个值为pivot value　　

#总是选取第一个值为pivot value

def quick_sort(alist,first,last):
    if first>=last:
        return None
    left = first+1
    right = last
    pivot = alist[first]
    while left<=right:
        while left<=right and alist[left]<=pivot:
            left = left+1
        while left<=right and alist[right]>=pivot:
            right = right-1
        if left<right:
            alist[left],alist[right]=alist[right],alist[left]
    alist[first],alist[right] = alist[right],alist[first]
    quick_sort(alist,first,right-1)
    quick_sort(alist,right+1,last)
alist=[1,9,2,88,98,76,67,49,105,6,10,6,47,8,7,20,32,34,21,23,16,12,10,38,43,89,102,260]
quick_sort(alist,0,len(alist)-1)
print(alist)  #0.017s

　　　基于随机值：列表中随机选取一个值为pivot value  （当排序列表较短时，随机算法花费时间长）

import random
def quick_sort2(alist,first,last):
    if first>=last:
        return None
    random_index = random.randint(first,last)  #随机选取一个数（）
    alist[first],alist[random_index]=alist[random_index],alist[first]
    left = first+1
    right= last
    pivot = alist[first]
    while left<=right:
        while left<=right and alist[left]<=pivot:
            left = left+1
        while left<=right and alist[right]>=pivot:
            right = right-1
        if left<right:
            alist[left],alist[right]=alist[right],alist[left]
    alist[first],alist[right] = alist[right],alist[first]
    quick_sort2(alist,first,right-1)
    quick_sort2(alist,right+1,last)

alist=[1,9,2,88,98,76,67,49,105,6,10,6,47,8,7,20,32,34,21,23,16,12,10,38,43,89,102,260]
quick_sort2(alist,0,len(alist)-1)
print(alist)    #耗费0.106s

　　　三路快排：从序列的first, middle, last三个元素中选择中间值（median of three)来做为pivot value

# #三路快排
def quick_sort3(alist,first,last):
    if first>=last:
        return None
    partition(alist,first,last)
    left = first+1
    right= last
    pivot = alist[first]
    while left<=right:
        while left<=right and alist[left]<=pivot:
            left = left+1
        while left<=right and alist[right]>=pivot:
            right = right-1
        if left<right:
            alist[left],alist[right]=alist[right],alist[left]
    alist[first],alist[right] = alist[right],alist[first]
    quick_sort3(alist,first,right-1)
    quick_sort3(alist,right+1,last)
def partition(alist,first,last):  #从alist[first],alist[mid],alist[last]三个中挑选中间值，并将其移动到alist[first]
    mid = (first+last)//2         
    if alist[first]>alist[last]:
        alist[first],alist[last] = alist[last],alist[first]
    if alist[mid]>alist[last]:
        alist[mid],alist[last] = alist[last],alist[mid]
    if alist[first]<alist[mid]:
        alist[first],alist[mid]=alist[mid],alist[first]
    #stprint alist[first],alist[mid],alist[last]
alist=[1,9,2,88,98,76,67,49,105,6,10,6,47,8,7,20,32,34,21,23,16,12,10,38,43,89,102,260]
quick_sort3(alist,0,len(alist)-1)
print(alist)  #耗时0.021s

　　　三路快排+插入排序：当排序序列较短时，利用插入排序的性能要比快速排序好，所以当递归的序列长度小于10（经验值）时可以用插入排序代替。

#三路快排+插入排序  （当排序数组较小时，插入排序的效率要高于快速排序）
def quick_sort4(alist,first,last):
    if (last-first+1)<10:                 #10为经验值？
        insert_sort(alist,first,last)
        return                          #记得return                          
    partition(alist,first,last)
    left = first+1
    right= last
    pivot = alist[first]
    while left<=right:
        while left<=right and alist[left]<=pivot:
            left = left+1
        while left<=right and alist[right]>=pivot:
            right = right-1
        if left<right:
            alist[left],alist[right]=alist[right],alist[left]
    alist[first],alist[right] = alist[right],alist[first]
    quick_sort4(alist,first,right-1)
    quick_sort4(alist,right+1,last)
def partition(alist,first,last):  #从alist[first],alist[mid],alist[last]三个中挑选中间值，并将其移动到alist[first]
    mid = (first+last)//2         
    if alist[first]>alist[last]:
        alist[first],alist[last] = alist[last],alist[first]
    if alist[mid]>alist[last]:
        alist[mid],alist[last] = alist[last],alist[mid]
    if alist[first]<alist[mid]:
        alist[first],alist[mid]=alist[mid],alist[first]
    #stprint alist[first],alist[mid],alist[last]
def insert_sort(alist,first,last):
    for i in range(first+1,last+1):
        pos = i
        cur = alist[i]
        while pos>first and alist[i]>cur:
            alist[pos]=alist[pos-1]
            pos = pos-1
        alist[pos]=cur                        
alist=[1,9,2,88,98,76,67,49,105,6,10,6,47,8,7,20,32,34,21,23,16,12,10,38,43,89,102,260]
quick_sort4(alist,0,len(alist)-1)
print(alist)    #耗时0.016s

3.总结

　　顺序查找：无论列表有序或无序，算法复杂度为O(n)

　　二分查找：适合有序列表的查找，最坏情况下算法复杂度为O(log n)

　　哈希查找：可以提供常量级别的算法复杂度O(k) （k为常数1,2,3.....）

　　冒泡排序，选择排序，插入排序：算法复杂度都为O(n²)

　　希尔排序：希尔排序在选择排序的基础上引入增量来分割子序列，算法复杂度在在O(n)—O(n²)之间，取决于增量的选择

　　归并排序：算法复杂度为O(n log n)，但排序过程中需要额外的存储空间

　　快速排序：快速排序的算法复杂度为O(n log n)，但若选择的分割点不是list的中间元素（取决于pivot value的选择），也可能变坏为O(n²)

 

参考：http://interactivepython.org/runestone/static/pythonds/SortSearch/toctree.html

　　　三种快速排序算法及其优化