递归算法（Recursion）

1，递归算法

　　递归算法是将复杂的问题分解为同类更简单的子问题，直到子问题可以被解决的算法思想。在下面的代码中，分别用普通方法和递归算法求list中数据累加之和，递归算法的求和过程如下图所示

#coding:utf-8

#普通方法
def listsum(numlist):
    total = 0
    for i in numlist:
        total = total+i
    return total

#递归算法
def recursionSum(numlist):
    if len(numlist)==1:
        return numlist[0]
    else:
        return numlist[0]+recursionSum(numlist[1:])

print listsum([1,3,5,7,9])
print recursionSum([1,3,5,7,9])

　　　　　　　 

 

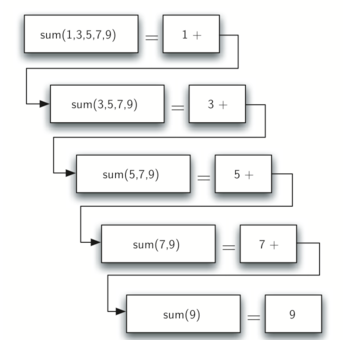
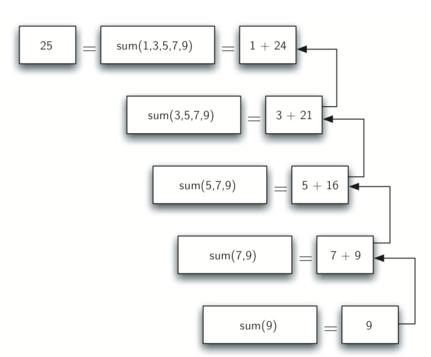
 　　可以发现递归算法遵循三条准则：

　　　　　1，递归算法必须有一个最基本的情况（出口）

　　　　　2，递归算法必须改变自身状态，并逐渐趋向于最基本情况

　　　　   3，递归算法必须递归的调用自身

2，递归算法应用

　　2.1 将整数转换为对应的2,8或16进制字符窜　　

#base可以为2,8,16
def toStr(num,base):
    convertString='0123456789ABCDEF'
    if num <base:
        return convertString[num]
    else:
        return toStr(num//base,base)+convertString[num%base]
s = toStr(12534,16)
print s, type(s)   #‘30F6’

 　　2.2 递归算法的可视化演示

　　　　利用python的turtle库，递归的画一棵树，代码如下：

#递归过程可视化
import turtle

def tree(branchLen,t):
    if branchLen > 5:
        t.forward(branchLen)
        t.right(20)
        tree(branchLen-15,t)
        t.left(40)
        tree(branchLen-15,t)
        t.right(20)
        t.backward(branchLen)

def main():
    t = turtle.Turtle()
    myWin = turtle.Screen()
    t.left(90)
    t.up()                 #画笔提起
    t.backward(100)         #向后退100
    t.down()                #画笔放下
    t.color("green")
    tree(75,t)
    myWin.exitonclick()

main()

　　　　利用python的turtle库，递归的画谢尔宾斯基三角形（Sierpinski triangle）,代码如下：

import turtle

def drawTriangle(points,color,myTurtle):
    myTurtle.fillcolor(color)
    myTurtle.up()
    myTurtle.goto(points[0][0],points[0][1])
    myTurtle.down()
    myTurtle.begin_fill()
    myTurtle.goto(points[1][0],points[1][1])
    myTurtle.goto(points[2][0],points[2][1])
    myTurtle.goto(points[0][0],points[0][1])
    myTurtle.end_fill()

def getMid(p1,p2):
    return ( (p1[0]+p2[0]) / 2, (p1[1] + p2[1]) / 2)

def sierpinski(points,degree,myTurtle):
    colormap = ['blue','red','green','white','yellow',
                'violet','orange']
    drawTriangle(points,colormap[degree],myTurtle)
    if degree > 0:
        sierpinski([points[0],
                        getMid(points[0], points[1]),
                        getMid(points[0], points[2])],
                   degree-1, myTurtle)
        sierpinski([points[1],
                        getMid(points[0], points[1]),
                        getMid(points[1], points[2])],
                   degree-1, myTurtle)
        sierpinski([points[2],
                        getMid(points[2], points[1]),
                        getMid(points[0], points[2])],
                   degree-1, myTurtle)

def main():
   myTurtle = turtle.Turtle()
   myWin = turtle.Screen()
   myPoints = [[-100,-50],[0,100],[100,-50]]
   sierpinski(myPoints,3,myTurtle)
   myWin.exitonclick()

main()

　　2.3 汉诺塔问题（Hanoi Tower）

　　假设有三个命名为 A B C 的塔座 ，在塔座A上插有n个直径大小不相同，由小到大编号为1 ，2 ，3 ，··· ，n的圆盘，要求将A座上的圆盘移至塔座C，并按同样的顺序叠排。

　　圆盘移动必须遵守下列规则： 1：每次只能移动一个圆盘； 2：圆盘可以插在任意一个塔座上； 3：任何时刻都不能将一个较大的圆盘放在一个较小的圆盘上。

　　下图为3阶汉诺塔：

　　 　　　　　　　　　　

　　递归过程：

　　　　1，借助塔座C，将n-1号圆盘从塔座A移动到塔座B

　　　　2，将塔座A上剩余的圆盘n，移动到塔座C

　　　　3，借助塔座A，将n-1号圆盘从塔座B移动到塔座C

　　代码实现如下：　

def moveTower(height,fromPole, toPole, withPole):
    disks=['small','medium','big']
    if height >= 1:
        moveTower(height-1,fromPole,withPole,toPole)
        moveDisk(fromPole,toPole,disks[height-1])
        moveTower(height-1,withPole,toPole,fromPole)

def moveDisk(fp,tp,disk):
    print "moving %s from %s to %s"%(disk,fp,tp)

moveTower(3,"A","B","C")

 

参考：http://interactivepython.org/runestone/static/pythonds/Recursion/toctree.html