信友队省选基础 · 贰
11/10
树分治。
点分治
算法本身没什么好说的。
POJ 1741
纯板子。但要注意排除来自同一棵子树的这种 不合法的 方案。全局跑一遍,局部分别跑一遍就 over 了。
BZOJ 2599
也很板子啊。
边分治
有时点分治写不了,就要用边分治。
菊花图会被卡,因此要优化建图一下。
可以证明三度化后递归深度是 \(O(\log n)\) 的。因为在重心旁边我们可以找到一条保证复杂度的边。底数大概是 \(3/2\)。这是因为三度化后重儿子的大小在 \(n/3\) 和 \(n/2\) 之间。
三度化方法有
-
线段树式:把儿子们用线段树的结构,用虚点连起来。
-
链式:书上看来的,开一条链,最顶上是这个点,每个链上的点挂一个儿子。
SPOJ Free Tour II
和上面那个题有啥区别。可以用树状数组维护一下,做到 \(O(n \log^2 n)\)。
然而我们在做题,因此思考去掉这个 \(\log\)!
一个不难的观察是黑点顶多 \(n\) 个,可以桶排序。但关键在于子树内部难处理。
哦哦,边分不就可以了?
于是可以 \(O(n \log n)\)。
哦哦哦,点分好像也是可以的,因为我们只要把子树按照 siz 排序(桶排序),这样每次更新就是 \(O(size)\) 的。于是总复杂度就是 \(O(n \log n)\)。总之这个思路有点像长链剖分优化 DP。
BZOJ 3784
统计多少条路径 \(\ge x\) 是好做的。那么二分一个边权限制就行了。单次是 \(O(n \log^2 n)\),那总复杂度就是三只 log 了。
但瓶颈在于点分治过程中的排序,因此把排序结果记下来就行了。
注意如果排序 vector 且用了基于 range 的 for 循环,一定要加 &!
动态点分治
ZJOI2007
点分树模板题,但是我要写吐了。
好像可以用边分树更简单的写。如果真是这样,岂不是我 200+ 行的点分树白写了???
upd: 终于过了 corner case。
HNOI2015
我怎么还做过了?
还可以用树剖 + 主席树做。可以考虑将全局 \(dis\) 变成 \(\sum dis_u + dis_v - 2 \times dis_{lca}\)。然后搞几下子,省略一堆过程就做完了。
此外还能用分块做。颜色排序分块,预处理整块到某个点的距离和,balabala...
这个用点分树做基于这个事实:点分树上的 LCA,在两点路径之间。
LibreOJ 6145
其实可以这样做:分治重心开个线段树记录点分树的子树内的点到它的距离。然后查询就是暴力每个都算一遍。
由于 \(\min\) 具有等幂性*,这样子是对的。
* 等幂性:\(\min(\min(a, b), b) = \min(a, b)\)。
上课讲得什么东西,我来补一遍正常的题解:
-
引理 1:记两点 \(u, v\) 路径上的点集为 \(S\),点分树上 \(u, v\) 的 LCA 为 \(l\),则 \(l \in S\)。
可以用反证法证明。
-
引理 2:记两点 \(u, v\) 路径上的点集为 \(S\),一定存在 \(l\),满足 \(l \in S\) 且在点分树上,\(lca(u, v) = l\)。
也可反证法。
因此,我们用动态开点线段树森林来维护点分子树内的信息。暴力往上跳,顺便查询就行了。
但看了下 LibreOJ 上的代码,貌似不用显式建点分树,点分治再 ST 表就行了?
ZJOI2015
Key Observation: 我们走到一个点,可以判断重心在哪里。就边都枚举一遍,看看哪边能走,否则定死了。
直接走,长度是 \(O(n)\) 的,但点分树上走一下,就只要 \(O(d \log n)\) 了,这正体现了点分树树高很小的优势。
最后答案的计算与上面那个 HNOI 是相似的。
WC2014 紫荆花之恋
首先,如果是个静态的,那么点分树随便做。
动态加少量 / 随机叶子,那我会暴力直接接上去!
关键就在于,可能树太高了,于是我们可以定期重构。类似替罪羊,当出现某子树超过父节点子树大小的 \(\alpha\) 倍时重构。
最后,平衡树巨难写,可以看 panyf 写的用 basic_string 实现的 \(O(n\sqrt{n})\) 的「缓存 vector」。
11/17
数据结构通常这么用:
-
利用本身结构。
-
利用数据结构优化某一过程。
例题
ARC073F
\(O(n^2)\) 的 dp 不难设计。注意到肯定有一个方块在 \(x_{i - 1}\)。
针对转移不难想出线段树优化。
CF671D

什么东西?
哦空间应该不会炸因为可并堆元素数量是 \(O(m)\) 的。
NOI2020 destiny

线段树合并没学过,如何听课?
空间也不会爆,因为线段树合并的空间是 \(O(\operatorname{info} \log n\) 的。
APIO2016 fireworks
抽象成函数,抽象的。
大概听懂干了些啥。
这种题被称为「维护凸函数的 trick」。(好怪的名字)
CF1129D

树形数据结构不好做就分块!
具体区间是,记 \(lst(a)\) 是 \(a\) 上一次出现 \(a\) 的位置,那 \(cnt([lst^{(2)}(a) + 1, lst(a) - 1], \cdot)\) 要减 \(1\),同理另外有一个区间也要加 \(1\)。
P6021
没有修改就是 tg 组 T1:\(d_u = \min(u, \sum f_v)\)。

上图的矩阵写反了,vector 应该在右边。
#546. grid
如果想到了第一步的缩,那整个题还是比较自然。但没想到/xk

补充练习
就是没讲的题。怎么都这么困难,玉玉了。
11/24
离线算法与数据结构。
常用方法:
-
扫描线
扫描,用数据结构维护另一维。
-
分治
-
莫队
IOI1998 Picture
入门题,当时好像调了好久。
JOISC 2014 Day3
经典分治题。之前在信友队做过了。
CERC2017

直接把图切割实在是太难做了!做了记下都把自己叉掉了!
那我们先时光倒流!变成合并!
不过在这之前,先算出最终状态的答案!
扫描线!

PA2014

下午再看看题解。最值分治(一种启发式分裂)可以 \(O(n \log n)\)。
启发式分裂是什么?分裂的复杂度是 \(\min(n - x, x)\) 的一种分治。
CF997E

什么鬼,又是没学过的。
P5163
无向图很好做。时光倒流,线段树合并。

Ynoi 2009
修改部分似乎可以 2D 线段树。然而查询的话 \(O(q \log^2 n)\) 应该是过不去的。
后面在讲啥啊。。。
APIO2018

后面那个判断方法真是巧妙,可以作为一个 trick。
JOISC2020
又没听懂。
12/01
公式
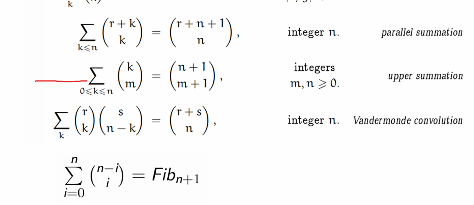
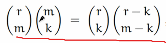
二项式定理
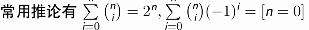
范德蒙德卷积

一些例题
子集异或的和
拆位,然后干啥不就太简单了。
排列
\(n, k \le 10^7\),问多少个排列满足 \(\forall i > k, p_i > \min(p_{i - k}, \dots, p_{i - 1})\)。

还是考虑最值 \(1\)。然后发现随意排布是关键。
GCD
给出一个 \({a_1, \dots, a_n}\),对于 \(g = 1, \dots, n}\) 输出多少个子集的 \(\gcd = g\)。

原来还能这么做。\(gcd\) 容易想到枚举倍数是 \(O(n \log n)\)。主要是 dp 想不出来。
鸽巢原理
差的绝对值之乘积模小模数
\(m \le 2000\),求 \(\prod \prod |a_i - a_j| \bmod m\)。
显然可以 \(O(m^2)\)。
和 = 和


卡特兰数
LGV
好像差不多听懂了一点。
12/08
最后一次课!最优化问题。
算法
程序 = 算法 + 数据结构
算法:指数级复杂度与完全不可做复杂度 \(\to\) 还行的 / AC 的多项式复杂度
数据结构:\(O(n) \to O(\log n)\)
算法解决什么问题?
-
求值
-
最优化
-
存在性
-
博弈论
-
……
模型
模型是什么?
-
散点,\(n\) 个没啥关系的东西,可以 sort
-
序列区间
-
tree
-
graph
-
string
-
数论、整数
-
网格图
-
集合
-
……
最优化算法
贪心,dp,二分,枚举,图论算法……
贪心 vs 动态规划
-
有明显阶段
贪心:每个阶段,选当前阶段最优解
DP:每个阶段枚举所有状态与决策,与暴力唯一的差别是归纳掉了无后效性的等价状态
-
贪心更快,DP 更对
Topcoder srm543

本质上,我们来描述这个题:(河岸很好处理,就先不管了)
这是什么?看看第一个式子,不就是一个优先队列维护的裸题吗?
\(O(Y \log N)\)
再加强
\(Y \le 10^9\)。
观察上面的过程。我们每次都是把小的取出来,往 heap 里塞一个大一点的东西。
因此取数有单调性,是个二分裸题。
\(O(N \log Y)\)
NOI2012 骑行川藏
得出 \(E_i\) 与 \(t_i\) 的关系,似乎就是上一题了!
某位 CSP AK 大神提出用什么拉格朗日算子法,太难了,ryz 没讲。
魔改(?)
这次求过河时间最大值。数据范围还是十万和十亿。
这回反而最 sb 了,就是只有一条河走斜线,别的横着。
魔改再魔改
这次一条河上最长只能走 \(u_i\) 米。
什么东西来着……
ZOJ3541
先正难则反。倒过来。
这样就容易了。
前边按了也是白按,所以只管最晚的。
这样子,按下的一定是区间,可以区间 DP。
XYD20436
 小的时候瞎暴力,大了的话就可以先到 \((2, 2)\),然后到 \((n, n - 2)\) 或 \((n - 1, n - 3)\)。
小的时候瞎暴力,大了的话就可以先到 \((2, 2)\),然后到 \((n, n - 2)\) 或 \((n - 1, n - 3)\)。
NOI2016
分析发现答案只能是 \(0, -1, 1, 2\)。这样就成了分类讨论题。
蛐蛐旁边的跳蚤才有用,因此建个图,常数大概 \(50 \sim 100\) 倍。
P10001
我谔谔,没听懂。
CF1510H
完全不懂。




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· NetPad:一个.NET开源、跨平台的C#编辑器
· PowerShell开发游戏 · 打蜜蜂
· 凌晨三点救火实录:Java内存泄漏的七个神坑,你至少踩过三个!