OMP

正交匹配追踪（OMP）：稀疏信号重建算法

动机：在处理稀疏信号时，每一个观测值其实都像是在给出“线索”，提示信号中最重要的几个分量在哪里。如果能够抓住这些线索，一步步把信号的主要特征找出来，就能在不依赖大量观测数据的情况下重建原始信号。因此，可以设想了一种方法：从残差中找出和当前最相关的方向，每次只添加一个最有信息量的分量，逐步逼近整个信号。这种“追踪线索”的方法既符合稀疏信号的特性，又让重建过程更高效。

---

引言：在稀疏信号处理中，正交匹配追踪（ OMP）是一种常用的重建算法。它能够在一定条件下以高效、准确的方式重建稀疏信号，并广泛应用于压缩感知和信号处理领域。本期将讲解 OMP 的基本原理、算法、应用实例，并探讨其在稀疏信号重建中的优劣。

正交匹配追踪的基本概念

OMP 是一种贪心算法，旨在通过逐步逼近原始信号的方式重建稀疏信号。对于一个稀疏信号 \(\mathbf{x}\)，我们假设其在某个基 \(\mathbf{D}\) 下可以表示为稀疏系数向量 \(\mathbf{\theta}\)，即：

\[\mathbf{x} = \mathbf{D} \mathbf{\theta} \]

其中，\(\mathbf{\theta}\) 仅包含少量非零元素。OMP 通过在基 \(\mathbf{D}\) 中寻找最接近原始信号的列，逐步选取并构建稀疏表示。

步骤

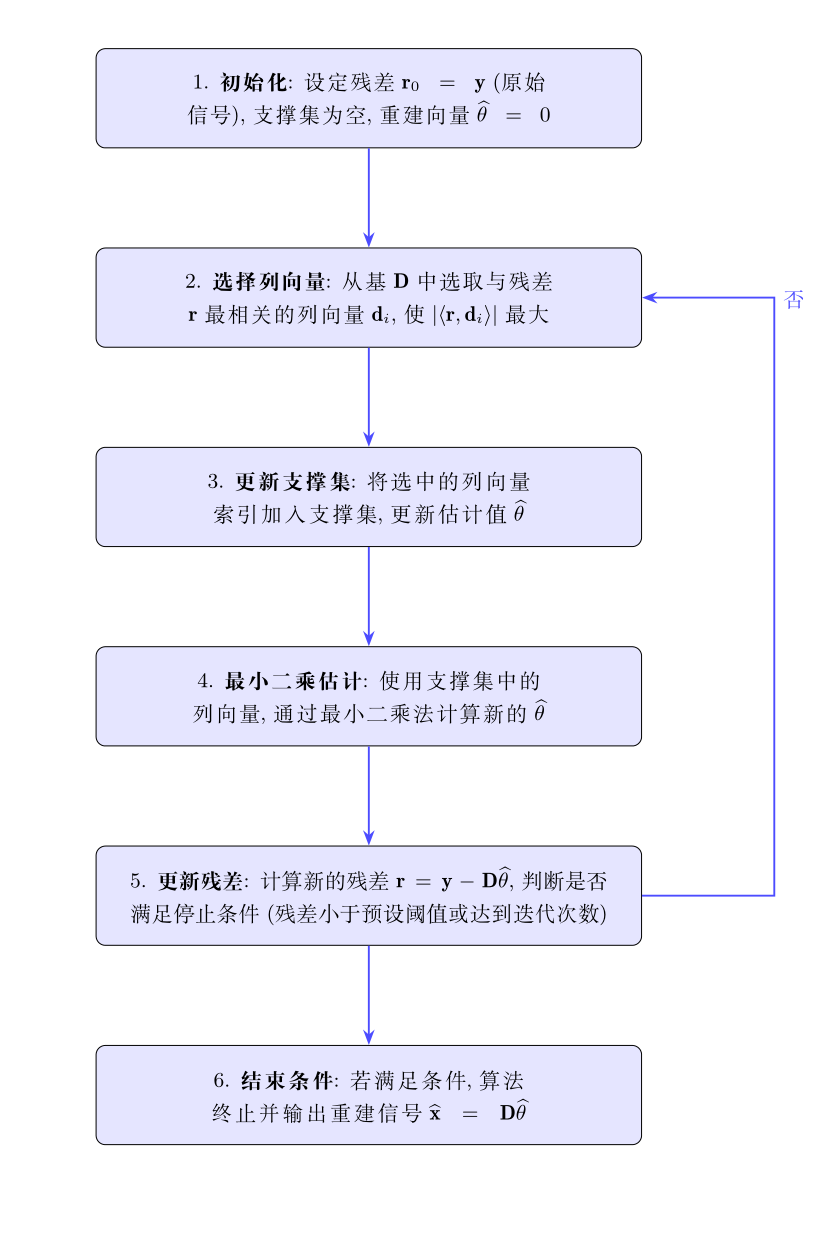
首先设定残差 \(\mathbf{r}_0 = \mathbf{y}\)（原始信号），初始化支撑集为空，重建向量 \(\mathbf{\hat{\theta}}\) 为零向量。并在每次迭代中，选择基 \(\mathbf{D}\) 中与残差 \(\mathbf{r}\) 最相关的列向量 \(\mathbf{d}_i\)。该向量使得 \(|\langle \mathbf{r}, \mathbf{d}_i \rangle|\) 最大。进而将选中的列向量的索引加入支撑集，同时更新估计值 \(\mathbf{\hat{\theta}}\)。利用当前支撑集中的列向量，通过最小二乘法计算新的估计向量 \(\mathbf{\hat{\theta}}\)。计算新的残差 \(\mathbf{r} = \mathbf{y} - \mathbf{D} \mathbf{\hat{\theta}}\)，判断是否满足停止条件（如残差小于预设阈值或迭代次数达到限制）。该算法在残差足够小或支撑集达到预设稀疏度时终止，最终输出重建信号 \(\mathbf{\hat{x}} = \mathbf{D} \mathbf{\hat{\theta}}\)。

实例

重建一个稀疏信号。设定信号 \(\mathbf{x}\) 具有稀疏性，即仅有少数元素非零。

import numpy as np
from sklearn.linear_model import OrthogonalMatchingPursuit
import matplotlib.pyplot as plt
from matplotlib import rcParams, font_manager

def find_chinese_font():
    font_list = font_manager.fontManager.ttflist
    for font in font_list:
        if "SimHei" in font.name:   
            return font.fname
        elif "SimSun" in font.name:   
            return font.fname
    return None

font_path = find_chinese_font()
if font_path:
    my_font = font_manager.FontProperties(fname=font_path)
else:
    print("未找到中文字体")

rcParams['axes.unicode_minus'] = False  
rcParams['font.size'] = 12   
rcParams['axes.linewidth'] = 1.2   
rcParams['xtick.direction'] = 'in'   
rcParams['ytick.direction'] = 'in'   

N = 100  
K = 5    
signal = np.zeros(N)
non_zero_indices = np.random.choice(N, K, replace=False)
signal[non_zero_indices] = np.random.randn(K)

M = 50   
phi = np.random.randn(M, N)
y = phi @ signal

omp = OrthogonalMatchingPursuit(n_nonzero_coefs=K)
omp.fit(phi, y)
reconstructed_signal = omp.coef_

plt.figure(figsize=(10, 6), dpi=300)  
plt.plot(signal, label="原始稀疏信号", color="navy", linewidth=2)
plt.plot(reconstructed_signal, linestyle="--", color="darkred", label="重建信号", linewidth=2)
if font_path:
    plt.legend(loc='upper right', fontsize=12, frameon=False, prop=my_font)  
    plt.xlabel("信号索引", fontsize=14, fontproperties=my_font)
    plt.ylabel("幅值", fontsize=14, fontproperties=my_font)
    plt.title("OMP 重建效果", fontsize=16, fontproperties=my_font)
else:
    plt.legend(loc='upper right', fontsize=12, frameon=False)  
    plt.xlabel("信号索引", fontsize=14)
    plt.ylabel("幅值", fontsize=14)
    plt.title("OMP 重建效果", fontsize=16)

plt.grid(True, linestyle='--', alpha=0.6)  
plt.tight_layout()  
plt.show()

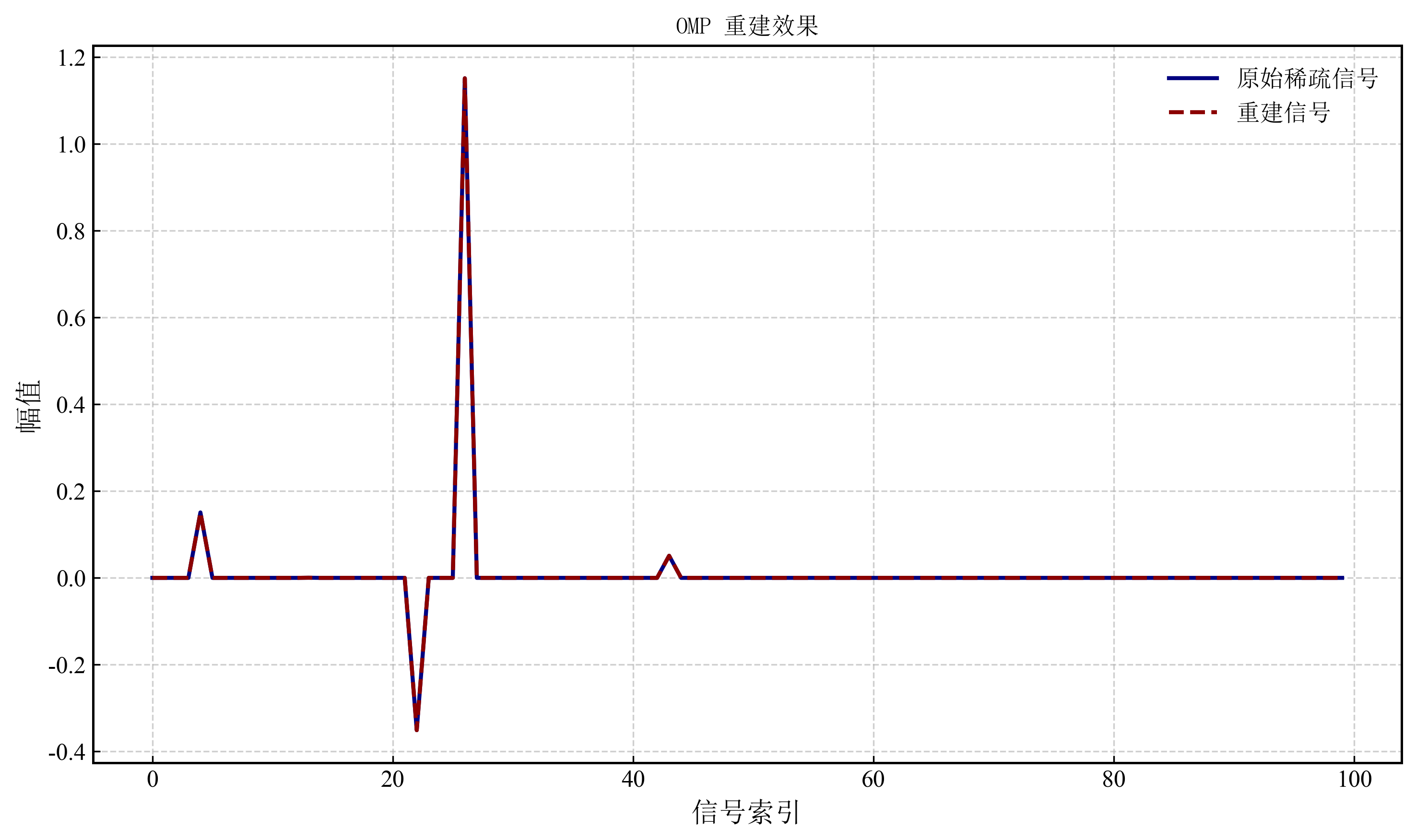
图1展示了使用正交匹配追踪（OMP）算法对稀疏信号的重建效果。蓝色实线代表原始稀疏信号，红色虚线为重建信号。可以看出，OMP 重建的信号在非零位置上与原始信号高度重合，说明算法成功识别了稀疏信号的非零位置和幅值。这表明在无噪声条件下，OMP 能够准确重建稀疏信号，重建精度高且未引入额外噪声或误差。

---

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams, font_manager

def orthogonal_matching_pursuit(phi, y, sparsity):
    N = phi.shape[1]
    residual = y.copy()
    index_set = []
    theta = np.zeros(N)

    for _ in range(sparsity):
        correlations = phi.T @ residual
        best_index = np.argmax(np.abs(correlations))
        index_set.append(best_index)
        phi_selected = phi[:, index_set]
        theta_selected, _, _, _ = np.linalg.lstsq(phi_selected, y, rcond=None)
        for i, idx in enumerate(index_set):
            theta[idx] = theta_selected[i]
        residual = y - phi @ theta
        if np.linalg.norm(residual) < 1e-6:
            break
    return theta

def find_chinese_font():
    font_list = font_manager.fontManager.ttflist
    for font in font_list:
        if "SimHei" in font.name:  
            return font.fname
        elif "SimSun" in font.name: 
            return font.fname
    return None

font_path = find_chinese_font()
if font_path:
    my_font = font_manager.FontProperties(fname=font_path)
else:
    print("未找到中文字体")

rcParams['axes.unicode_minus'] = False  
rcParams['font.size'] = 12
rcParams['axes.linewidth'] = 1.2
rcParams['xtick.direction'] = 'in'
rcParams['ytick.direction'] = 'in'

N = 100  
M = 50   
phi = np.random.randn(M, N)

# 1. 对噪声敏感性实验
noise_levels = [0, 0.05, 0.1, 0.2, 0.5, 1]  
K = 5  
signal = np.zeros(N)
signal[np.random.choice(N, K, replace=False)] = np.random.randn(K)

plt.figure(figsize=(12, 8), dpi=300)
for i, noise_level in enumerate(noise_levels, 1):
    y = phi @ signal + noise_level * np.random.randn(M)
    reconstructed_signal = orthogonal_matching_pursuit(phi, y, sparsity=K)
    
    plt.subplot(2, 3, i)
    plt.plot(signal, label="原始信号", color="navy", linewidth=1.5)
    plt.plot(reconstructed_signal, linestyle="--", color="darkred", label="重建信号", linewidth=1.5)
    plt.title(f"噪声水平: {noise_level}", fontproperties=my_font)
    plt.legend(prop=my_font)

plt.suptitle("OMP 对不同噪声水平的重建效果", fontproperties=my_font, fontsize=16)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

# 2. 稀疏度依赖性实验
estimated_sparsities = [2, 5, 7, 10, 15, 20]  
y = phi @ signal  

plt.figure(figsize=(12, 8), dpi=300)
for i, estimated_K in enumerate(estimated_sparsities, 1):
    reconstructed_signal = orthogonal_matching_pursuit(phi, y, sparsity=estimated_K)
    
    plt.subplot(2, 3, i)
    plt.plot(signal, label="原始信号", color="navy", linewidth=1.5)
    plt.plot(reconstructed_signal, linestyle="--", color="darkred", label="重建信号", linewidth=1.5)
    plt.title(f"预设稀疏度: {estimated_K}", fontproperties=my_font)
    plt.legend(prop=my_font)

plt.suptitle("OMP 对不同预设稀疏度的重建效果", fontproperties=my_font, fontsize=16)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

# 3. 适用范围实验（不同信号稀疏度）
true_sparsities = [2, 5, 10, 15, 20, 30]  

plt.figure(figsize=(12, 8), dpi=300)
for i, current_K in enumerate(true_sparsities, 1):
    signal = np.zeros(N)
    signal[np.random.choice(N, current_K, replace=False)] = np.random.randn(current_K)
    y = phi @ signal
    reconstructed_signal = orthogonal_matching_pursuit(phi, y, sparsity=current_K)
    
    plt.subplot(2, 3, i)
    plt.plot(signal, label="原始信号", color="navy", linewidth=1.5)
    plt.plot(reconstructed_signal, linestyle="--", color="darkred", label="重建信号", linewidth=1.5)
    plt.title(f"信号稀疏度: {current_K}", fontproperties=my_font)
    plt.legend(prop=my_font)

plt.suptitle("OMP 对不同信号稀疏度的重建效果", fontproperties=my_font, fontsize=16)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

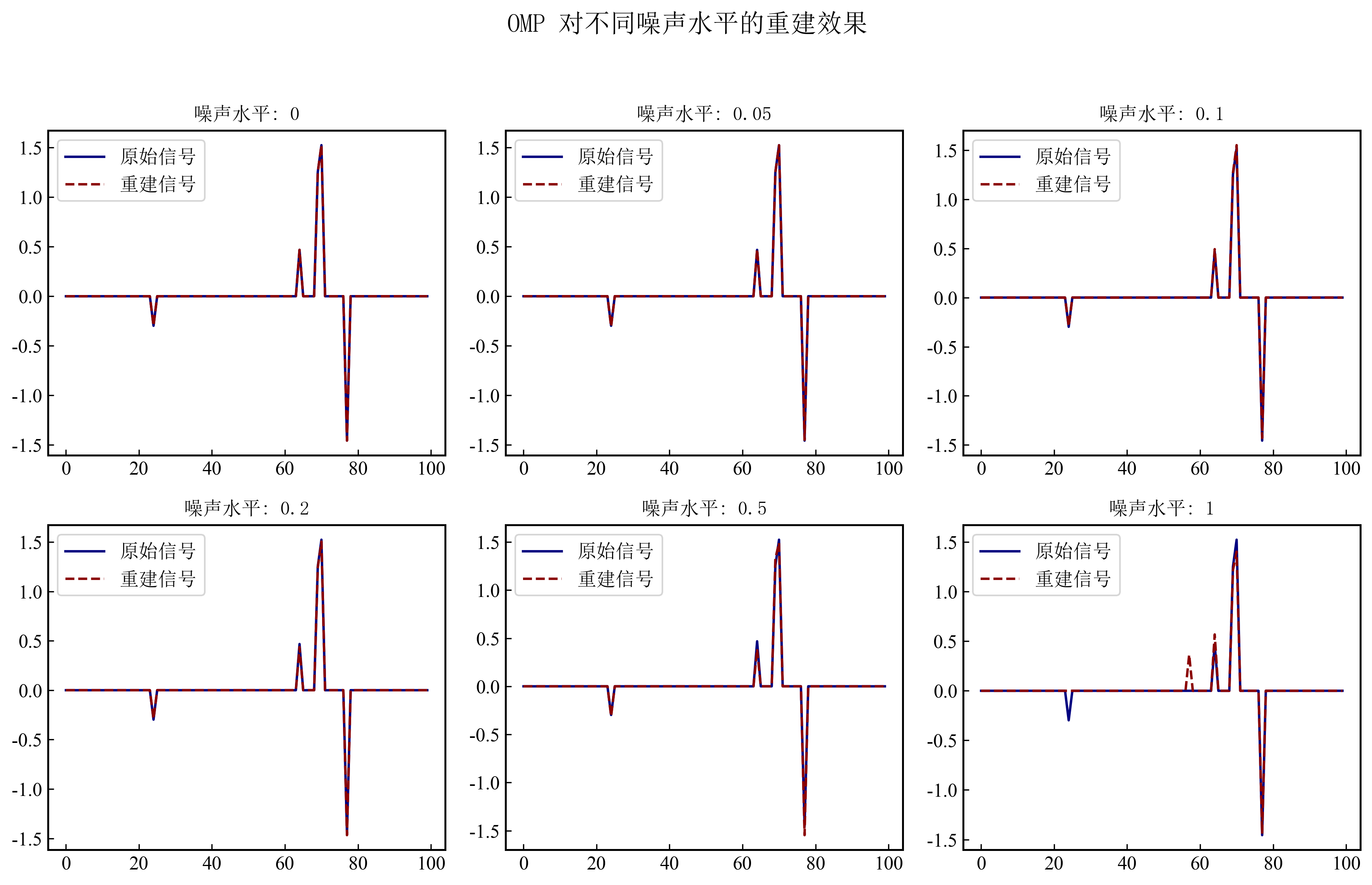
从图2可以看出，随着噪声水平的增加，OMP 的重建效果逐渐恶化。当噪声水平较低（如 0 和 0.05）时，重建信号与原始信号基本重合，说明 OMP 能够在低噪声条件下准确恢复稀疏信号。然而，当噪声水平较高时（如 0.5 和 1），重建信号开始出现明显偏差，甚至在部分位置出现错误的重建。这表明 OMP 对噪声较为敏感，噪声的存在会干扰其对稀疏分量的正确定位，导致重建质量下降。因此，在噪声较大的应用场景中，OMP 可能无法提供可靠的重建结果。

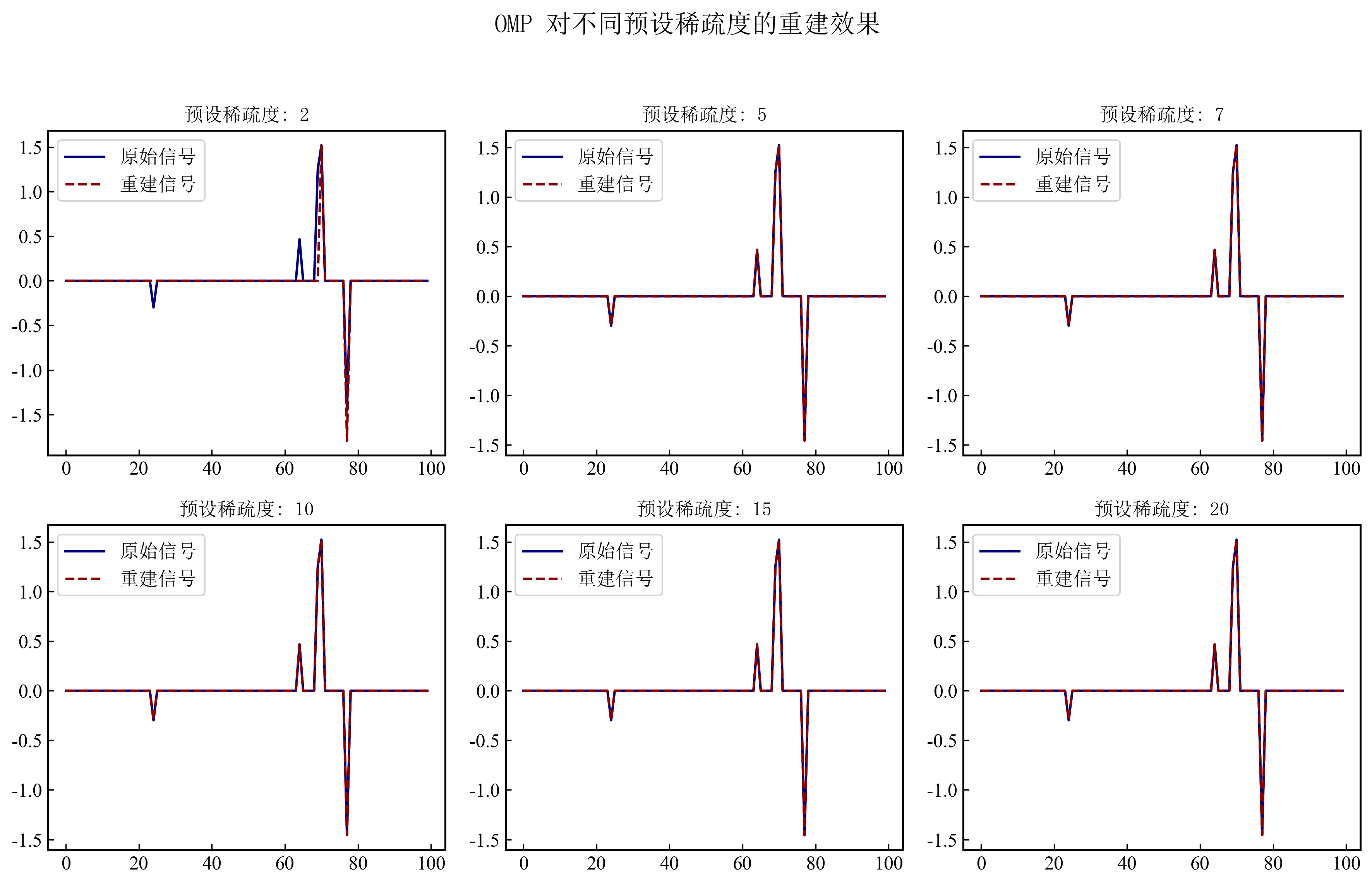
图3展示了 OMP 对预设稀疏度的依赖性。当预设稀疏度接近真实稀疏度（如 5 和 7）时，OMP 的重建效果较好，重建信号与原始信号基本一致。然而，当预设稀疏度低于真实值（如 2）时，重建信号缺少部分稀疏分量，导致信息丢失；而当预设稀疏度高于真实值（如 15 和 20）时，OMP 引入了多余的分量，导致重建信号中出现额外的噪声。这说明 OMP 对稀疏度参数的设定有较高要求。在实际应用中，如果信号的稀疏度未知，OMP 的重建效果可能会受到限制，导致精度下降。

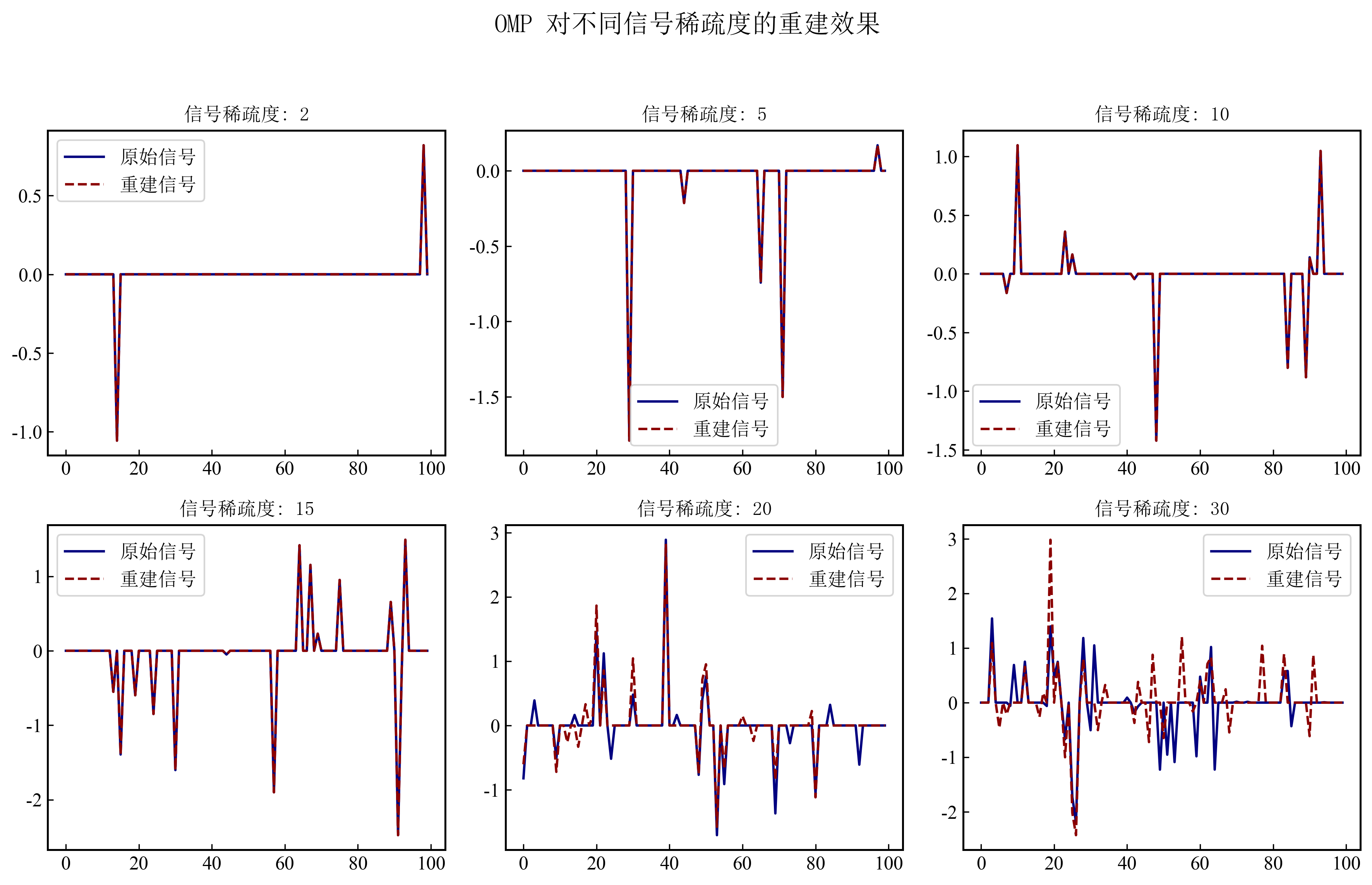
图4显示了 OMP 在不同信号稀疏度下的重建表现。当信号稀疏度较低（如 2 和 5）时，OMP 能够准确重建信号，重建效果良好；然而，当稀疏度增加（如 15 和 20）时，重建信号逐渐偏离原始信号；当稀疏度达到 30 时，OMP 的重建效果显著下降，出现明显的偏差。这表明 OMP 适用于低稀疏度信号，在信号稀疏度较高时，其重建能力会明显降低。因此，OMP 更适合用于处理稀疏分量较少的信号，而在非稀疏或高稀疏度信号的重建中效果不佳。

小结

正交匹配追踪（OMP）在稀疏信号处理中提供了一种快速、有效的重建方法。它通过贪心策略逐步逼近信号，有效应用于压缩感知和信号处理等领域。然而，OMP 也对信号稀疏度和噪声敏感，因此在实际应用中需根据具体情况选择合适的重建算法。

---