算法思想篇（1）————枚举算法

枚举算法的思想是：将问题的所有可能的答案一一列举，然后根据条件判断此答案是否合适，保留合适的，丢弃不合适的。在C语言中，枚举算法一般使用while循环实现。使用枚举算法解题的基本思路如下所示。
（1）确定枚举对象、枚举范围和判定条件；
（2）逐一枚举可能的解，验证每个解是否是问题的解。
枚举算法一般按照如下三个步骤进行。
（1）题解的可能范围，不能遗漏任何一个真正解，也要避免有重复。
（2）判断是否是真正解的方法。
（3）使可能解的范围降至最小，以便提高解决问题的效率。
用两个例子说明枚举算法的思想：
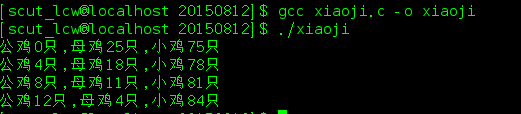
（1）百钱买百鸡问题：公鸡每只5元，母鸡每只3元，小鸡3只1元，用100块钱买100只鸡，问公鸡，母鸡，小鸡各多少只？
以上问题可以用如下代码解决

//start from the very beginning,and to create greatness
//@author: Chuangwei Lin
//@E-mail：979951191@qq.com
//@brief： 百钱买百鸡问题
#include <stdio.h>
int main()
{
    int x,y,z;//三个变量分别为公鸡，母鸡，小鸡的数量
    for(x=0;x<=20;x++)//公鸡最多20只
    {
        for(y=0;y<=33;y++)//母鸡最多33只
        {
            z=100-x-y;//小鸡的数量
            if (z%3==0 && x*5+y*3+z/3==100)//小鸡3只一元，所以小鸡数量应该是3的倍数
                printf("公鸡%d只,母鸡%d只,小鸡%d只\n",x,y,z);
        }
    }  
    return 0;
}

运行结果如下：

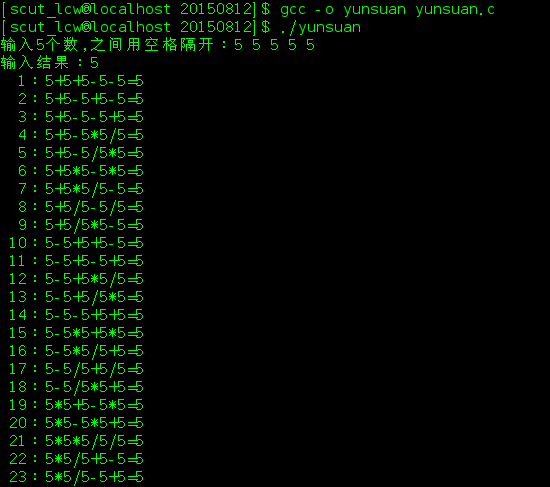
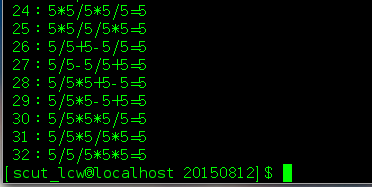
（2）填写运算符问题
在下面的算式中，添加+-*/4个运算符，使这个等式成立：5 5 5 5 5 = 5
代码如下：

//start from the very beginning,and to create greatness
//@author: Chuangwei Lin
//@E-mail：979951191@qq.com
//@brief： 运算符填写
#include <stdio.h>
int main()
{
    int j,i[5]; //循环变量 ，数组i用来表示4个运算符 
    int sign;//累加运算时的符号   
    int result; //保存运算式的结果值 
    int count=0; //计数器，统计符合条件的方案 
    int num[6];  //保存操作数 
    float left,right; //left用于保存上一步运行的结果，right用于保存下一步的结果
    char oper[5]={' ','+','-','*','/'}; //运算符 
    printf("输入5个数,之间用空格隔开：");
    for(j=1;j<=5;j++)
        scanf("%d",&num[j]);//5个数放在num数组里,注意第一个数放在num[1]
    printf("输入结果：");
    scanf("%d",&result);
    //开始填运算符
    for(i[1]=1;i[1]<=4;i[1]++)//循环4种运算符，1表示+，2表示-,3表示*，4表示/，这里是第一个运算符
    {
        if((i[1]<4) || (num[2]!=0))//运算符若是/,则第二个运算数不能为0
        {
            for(i[2]=1;i[2]<=4;i[2]++)//第二个运算符
            {
                if((i[2]<4) || (num[3]!=0))
                {
                    for(i[3]=1;i[3]<=4;i[3]++)//第三个运算符
                    {
                        if((i[3]<4) || num[4]!=0)
                        {
                            for(i[4]=1;i[4]<=4;i[4]++)//第四个运算符
                            {
                                if((i[4]<4) || (num[5]!=0))
                                {
                                    left=0;
                                    right=num[1];//取第一个数
                                    sign=1;
                                    for(j=1;j<=4;j++)
                                    {
                                        switch(oper[i[j]])//前面已经填好了运算符，现在取出来运算
                                        {//这样可以实现运算符优先级的运算
                                            //运算符只是先定下来，真正实现运算是在下一步，因为还要判断下一步是否优先级更高
                                            //若是乘和除就可以直接运算
                                            case '+': 
                                                 left=left+sign*right;
                                                 sign=1;
                                                 right=num[j+1];//取下一个数
                                                 break;
                                            case '-': 
                                                 left=left+sign*right;
                                                 sign=-1;
                                                 right=num[j+1];//取下一个数
                                                 break;//通过f=-1实现减法
                                            case '*': 
                                                 right=right*num[j+1];
                                                 break;//实现乘法
                                            case '/': 
                                                 right=right/num[j+1];//实现除法
                                                 break;
                                        }
                                    }
                                    if(left+sign*right==result)//若结果满足
                                    {
                                        count++;//满足的方案数加1
                                        printf("%3d：",count);//输出方案数
                                        //输出运算式
                                        for(j=1;j<=4;j++)
                                            printf("%d%c",num[j],oper[i[j]]);
                                        printf("%d=%d\n",num[5],result);
                                    } 
                                }
                            }
                        }
                    }
                }
            }
        }
    }
    if(count==0)//若没有符合条件的
        printf("没有符合要求的方法！\n");
    return 0;
}

结果如下：