算法思想篇（7）————迭代算法

迭代算法是用计算机解决问题的一种基本方法。它利用计算机运算速度快、适合做重复性操作的特点，让计算机对一组指令（或一定步骤）进行重复执行，在每次执行这组指令（或这些步骤）时，都从变量的原值推出它的一个新值。
在使用迭代算法解决问题时，需要做好如下三个方面的工作。
（1）确定迭代变量
在可以使用迭代算法解决的问题中，至少存在一个迭代变量，即直接或间接地不断由旧值递推出新值的变量。
（2）建立迭代关系式
迭代关系式是指如何从变量的前一个值推出其下一个值的公式或关系。通常可以使用递推或倒推的方法来建立迭代关系式，迭代关系式的建立是解决迭代问题的关键。
（3）对迭代过程进行控制
在编写迭代程序时，必须确定在什么时候结束迭代过程，不能让迭代过程无休止地重复执行下去。通常可分为如下两种情况来控制迭代过程：
所需的迭代次数是个确定的值，可以计算出来。可以构建一个固定次数的循环来实现对迭代过程的控制；
所需的迭代次数无法确定，需要进一步分析出用来结束迭代过程的条件。
下面通过一个简单的例子说明迭代算法的思想：
使用迭代算法求平方根的问题：输入一个数，利用迭代算法求其平方根
代码如下：

//start from the very beginning,and to create greatness
//@author: Chuangwei Lin
//@E-mail：979951191@qq.com
//@brief： 迭代算法求平方根的问题
#include <stdio.h>
#include <math.h>
void main()
{
    double a,x0,x1;
    printf("请输入一个大于0的数:\n");
    scanf("%lf",&a);
    if(a<0)
        printf("输入的数要大于0!\n");
    else 
    {
        x0=a/2;//首先设a/2为平方根的初值
        x1=(x0+a/x0)/2;//利用迭代公式求平方根
        do//循环迭代
        {
            x0=x1;
            x1=(x0+a/x0)/2;
        }while(fabs(x0-x1)>=1e-6);//迭代一直到x0于x1的差的绝对值满足指定的精度
    }
    printf("结果如下:sqrt(%g)=%g\n",a,x1);
}

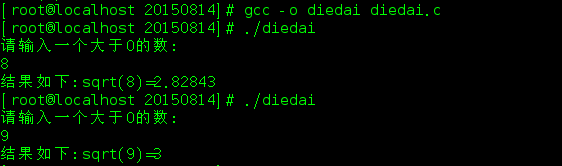
运行结果如下：