项目应用中的卡尔曼滤波

接触卡尔曼滤波的渊源

最近因为项目需要，需要对经某种途径获取到的数据进行处理，数据大概就是从某种传感器那里来的，现在假定这个数据是某个网络的阻抗。获取到数据之后，发现数据是波动的，并且波动的范围比较大，我将数据记录后使用excel绘出图形，发现数据好像是周期性波动的。在这种情况下我首先想到的便是一阶滞后滤波，因为之前有项目用到过，但是效果不是很理想(可能因为某些参数调的不对)，使用均值滤波后的值也是波动很大的，所以就在思考换别的滤波方式。卡尔曼滤波之前就有听到过的，所以自然想来试一试。

从阻抗到卡尔曼

卡尔曼滤波器可以从数据序列中排除干扰噪声，使用卡尔曼滤波器可以从不完整的信息给出一个不断变化中复杂系统的最优估计。为了可以更好地理解卡尔曼滤波器，这里使用一种形象的描述方法来说明，最后我会在底下附上其数学的推导（其实也是为了让我自己能更加深入理解）。在网上找到的例子，大都是那个测量温度的例子，或者是某大神从牛顿第二定律到卡尔曼的理解。这里我就按照我要测量的阻抗，写出自己的理解（所以我也不知道对不对）。本文讲的卡尔曼滤波器都是最简单的一维（标量）的卡尔曼滤波器。

---

我们把某种网络抽象为一个电阻，现在我们要用传感器（当然不是简单的万用表欧姆档测电阻哈）测量该电阻的阻抗。根据经验判断，如果测量的频率不变的话，阻抗应该是不变的。所以我们认为，下一分钟的阻抗应该是等于现在的阻抗的。但是我们的经验可能不是百分之百准确，阻抗可能会由于环境温度啊什么其他的原因而稍有偏差，我们把这样的偏差看成高斯白噪声，意味着这些偏差跟前后时间没有关系并且符合高斯分布。
现在假设我们有一个万用表，但是这个万用表是很不准确的（就像我们实验室里的万用表。。。。），测量值和真实值之间总是会存在偏差，我们也把这些偏差看成高斯白噪声。
现在对于这一个时刻我们有了两个关于该电阻的阻抗：一个是根据我们的预测（可以认为根据标称值预测）和用万用表测得的值。这两个值分别称为系统的预测值和测量值。
现在我们要估算k时刻该电阻的实际阻抗。首先我们要根据k-1时刻的阻抗值，来预测k时刻的阻抗值。因为我们认为阻抗是不变的。所以我们预测的k时刻的阻抗值和k-1时刻的阻抗值应该是一样的，假设为99欧姆，同时该值的高斯白噪声的偏差为5（假设的，卡尔曼是递归的，5可以这样理解，k-1时刻估算的最优阻抗值的偏差是3，我们的预测的不确定度是4，两者平方和在开方）。另外，我们用万用表也测出一个阻抗的值，假设为103欧姆，偏差是3。
所以现在我们真的有了两个阻抗值，分别是99欧姆和103欧姆。那么实际的阻抗究竟是多少呢？是我们的预测准确还是不靠谱的万用表准确呢？我们可以使用协方差covariance来判断。假设万用表的协方差比较小（虽然万用表不一定准但是我觉得很多人还是比较相信万用表）。并且假设真实阻抗可以这么算得：

系数：Kg2=52/(52+42)=0.78真实阻抗：99+0.78∗(103−99)=102.12

因为万用表的协方差比较小，所以真实阻抗更加近测量值。
k时刻的最优阻抗值我们已经知道，现在就要进入k+1时刻，进行新的最优估算。这里也就是卡尔曼自回归的地方，先计算k时刻最优值（102.12）的偏差：((1-Kg^2)*5^2)^0.5=2.35。这里的5就是之前预测的偏差，得出的2.35就是进入k+1时刻后k时刻估算出的最优阻抗值的偏差（对应于上面的3）。
卡尔曼滤波就是这样不断把协方差递归，从而估算出最优的阻抗值。运行速度很快，并且只保留了上一时刻的协方差，上面的Kg，其实就是对应着卡尔曼增益，可以随不同的时刻而改变自己的值。

卡尔曼滤波器

卡尔曼滤波其实就是5条公式。任何伟大的理论最后的表现形式都是极其简单的，卡尔曼滤波器也是这样。
首先，我们先要引入一个离散控制过程的系统。该系统可表述为下面的差分方程：

X(n)=AX(n−1)+BU(n−1)+W(n−1)

假设X(n)不可以直接测得，可以测的是另一个量Z(n)

Z(n)=HX(n)+V(n)

上面的两个式子中，X(n)是n时刻的系统状态量，U(n)是n时刻对系统的控制量。A和B是系统参数，对于多模型系统，他们为矩阵。Z(n)是n时刻的测量值，H是测量系统的参数，对于多测量系统，H为矩阵。W(n)和V(n)分别表示过程和测量的噪声。他们被假设成高斯白噪声(White Gaussian Noise)，服从高斯分布，covariance 分别是Q，R（这里我们假设他们不随系统状态变化而变化）。

现在要考虑的是如何从可观测量Z(n)的观测数据中得出X(n)的最优估计值，并把噪声W(n)和V(n)尽最大可能过滤出去，把他们的影响降到最小。对于满足线性随机的微分系统，过程和测量都是高斯白噪声，卡尔曼滤波器对此是最优的信息处理器。
这里首先要明白两个概念
对一个随机变量当前的先验估计是根据前一个时刻以及更早的历史观测信息所作出的估计，后验估计是根据当前时刻以及更早的历史观测信息所作出的估计，我更喜欢这种表示方式，例如

X(n)在n时刻的先验估计表示为X(n|n−1)，X(n)在n时刻的后验估计表示为X(n|n)

第一步：时间更新

预测系统状态
卡尔曼滤波器按照先验估计给出新的时间点的估计值，X(n)的先验估计是由上一个时间点的后验估计值和输入信息给出的

X(n|n−1)=AX(n−1|n−1)+BU(n)………..(1)

式(1)中，X(n|n-1)是利用上一状态预测得的结果，X(n-1|n-1)是上一状态最优的结果，U(n)为现在状态的控制量，如果没有控制量，它可以为0。
预测系统协方差
到现在为止，我们的系统结果已经更新了，可是，对应于X(n|n-1)的协方差还没更新。我们用P表示协方差，有：

P(n|n−1)=AP(n−1|n−1)A′+Q………(2)

式(2)中，P(n|n-1)是X(n|n-1)对应的协方差，P(n-1|n-1)是X(n-1|n-1)对应的协方差，A’表示A的转置矩阵，Q是系统过程的协方差

第二步：测量更新

将新的时间点的实际测量值加入到算法中，滤波器按照此值修正卡尔曼增益，并给出后验估计值。
修正卡尔曼增益

Kg(n)=P(n|n−1)H′/(HP(n|n−1)H′+R)………(3)

修正系统状态
(1)式得到的是现在状态的预测结果即X(n|n-1)，现在状态的测量值是Z(n)。结合预测值和测量值，我们可以得到现在的最优化估算值X(n|n)：

X(n|n)=X(n|n−1)+Kg(n)(Z(n)−HX(n|n−1))………(4)

修正系统协方差
得到了n状态下最优的估算值X(n|n)后，为了要让卡尔曼滤波器不断的运行下去直到系统过程结束，我们还要更新n状态下X(n|n)的协方差：

P(n|n)=（I−Kg(n)H）P(n|n−1)………(5)

上面就是卡尔曼滤波器的5条公式，由这五条公式不断修正和递归运算直到系统结束。由这5条公式来实现卡尔曼滤波器还算是比较简单的，看语言实现的话理解也会快很多，下面实现一个最简单的一维的卡尔曼滤波器。

用C语言实现的一维卡尔曼滤波器

我们用一个结构体来保存卡尔曼滤波器的所有系数，因为有些系数是需要递归下去的，所以每个卡尔曼滤波器用一个结构体来描述，传参的时候要传地址。又因为是一维的卡尔曼，上面5条公式中所有的矩阵全部退化为标量。
卡尔曼滤波器结构体如下：

//1维的卡尔曼滤波
typedef struct {
    float x;  // 系统的状态量 
    float A;  // x(n)=A*x(n-1)+u(n),u(n)~N(0,q) 
    float H;  // z(n)=H*x(n)+w(n),w(n)~N(0,r)   
    float q;  // 预测过程噪声协方差
    float r;  // 测量过程噪声协方差 
    float p;  // 估计误差协方差
    float gain;//卡尔曼增益
}kalman_struct;

滤波器实现如下：

/**
 *kalman_init - 卡尔曼滤波器初始化
 *@kalman_lcw：卡尔曼滤波器结构体
 *@init_x：待测量的初始值
 *@init_p：后验状态估计值误差的方差的初始值
 */
void kalman_init(kalman_struct *kalman_lcw, float init_x, float init_p)
{
    kalman_lcw->x = init_x;//待测量的初始值，如有中值一般设成中值
    kalman_lcw->p = init_p;//后验状态估计值误差的方差的初始值
    kalman_lcw->A = 1;
    kalman_lcw->H = 1;
    kalman_lcw->q = ？;//预测（过程）噪声方差 实验发现修改这个值会影响收敛速率
    kalman_lcw->r = ？;//测量（观测）噪声方差
    //这里两个参数是最关键的
}

/**
 *kalman_filter - 卡尔曼滤波器
 *@kalman_lcw:卡尔曼结构体
 *@measure；测量值
 *返回滤波后的值
 */
float kalman_filter(kalman_struct *kalman_lcw, float measure)
{
    /* Predict */
    kalman_lcw->x = kalman_lcw->A * kalman_lcw->x;
    kalman_lcw->p = kalman_lcw->A * kalman_lcw->A * kalman_lcw->p + kalman_lcw->q;  /* p(n|n-1)=A^2*p(n-1|n-1)+q */

    /* Measurement */
    kalman_lcw->gain = kalman_lcw->p * kalman_lcw->H / (kalman_lcw->p * kalman_lcw->H * kalman_lcw->H + kalman_lcw->r);
    kalman_lcw->x = kalman_lcw->x + kalman_lcw->gain * (measure - kalman_lcw->H * kalman_lcw->x);
    kalman_lcw->p = (1 - kalman_lcw->gain * kalman_lcw->H) * kalman_lcw->p;

    return kalman_lcw->x;
}

这里假设系统没有控制量，所以之前U(n)那一项这里是0，其中函数kalman_filter就是将那五条公式实现了一番，要注意C语言里面好像是不能直接计算矩阵的，如果是矢量的卡尔曼滤波应该要先转换好。这里的程序很容易理解，使用也很简单。

项目应用中的卡尔曼滤波

卡尔曼的实现虽然很简单，但是其调参却是大有学问。主要需要设定的参数如下：
init_x：待测量的初始值，如有中值一般设成中值
init_p：后验状态估计值误差的方差的初始值
q：预测（过程）噪声方差
r：测量（观测）噪声方差。
其中init_x和init_p的值是猜测的，对于卡尔曼滤波算法来说，这两个值是否准确并不十分重要。当然应该避免把方差的猜测值选为0或者太小，太大的的情况，因为那样会使算法误解。
因为我是测量阻抗，前面也说了阻抗一般是不会变的，所以A我自然是取1，大部分情况下，如果物理量能直接通过传感器测量，那么H取1，至于
init_x和init_p，可以先随便取两个值，我觉得最好是和你的数据差不多的值。q和r我觉得是最重要的两个参数。网上很多的说法是要靠经验还有实验来调。r是测量（观测）噪声方差，网上有个做法，以陀螺仪为例：保持陀螺仪不动，统计一段时间内的陀螺仪输出数据。数据会近似正态分布，按3σ原则，取正态分布的(3σ)^2作为r的初始化值。
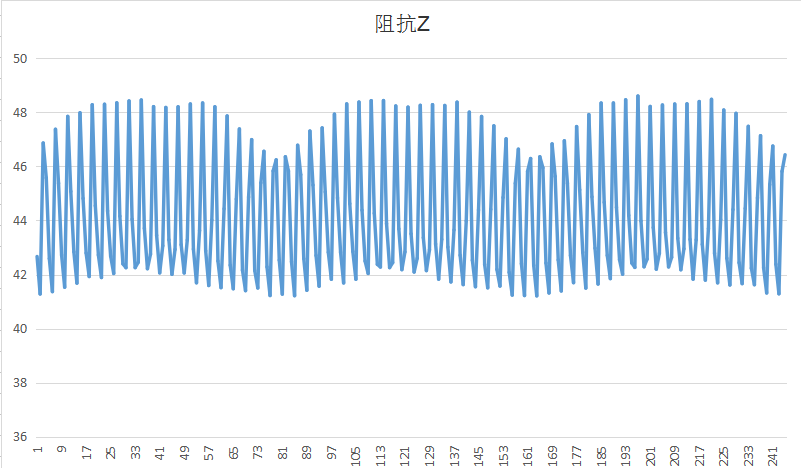
我将原始数据保存后，用execl画图，因为这个没有经过均值滤波的，比较夸张

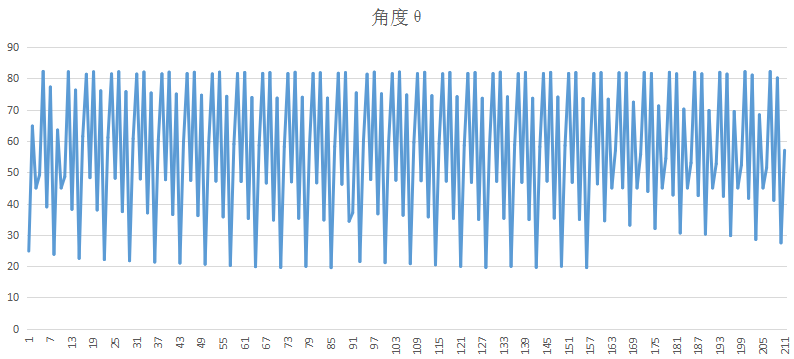
另一个量

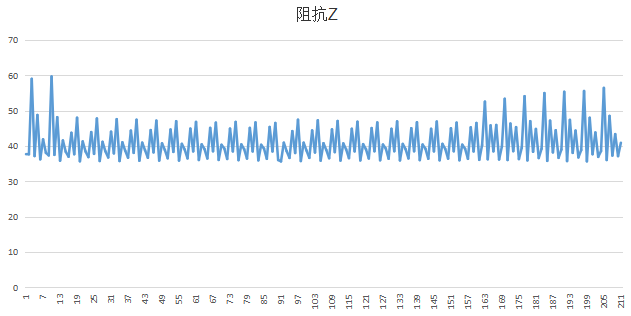
卡尔曼滤波的参数调的不恰当的时候，并不能发挥其作用
下面是最初做的卡尔曼滤波的结果


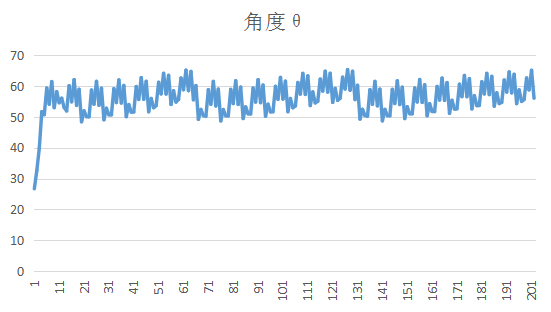
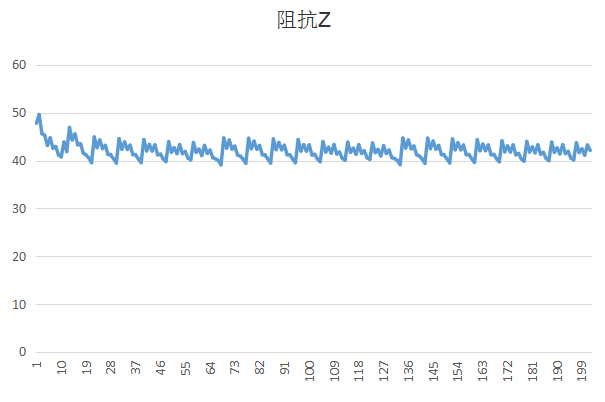
效果不是很满意，我在网上查了某MPU6050模块的滤波结果图
滤波前

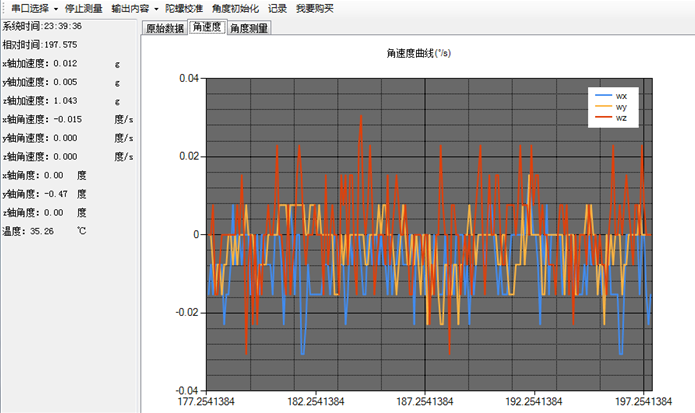
滤波后

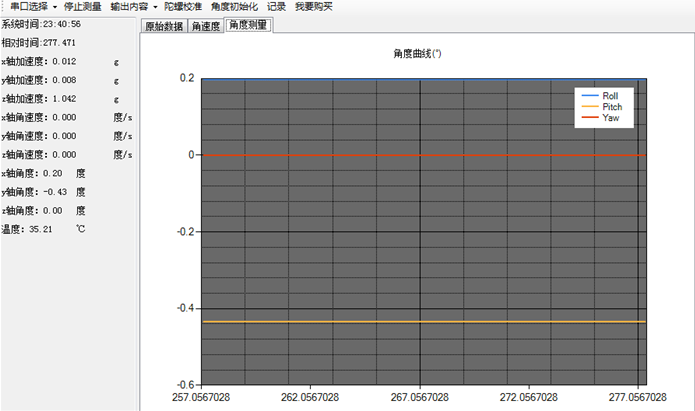
看完之后觉得有点神奇有点夸张，同时也是持着怀疑的态度我又接着调参数（虽然显然我的原始数据比他的波动要大很多）。
实验过程中我发现init_x和init_p的值比较无关紧要其实是因为卡尔曼滤波是收敛的，最终会收敛到一个值。因为卡尔曼是最优化迭代自回归算法，其中好像只有q和r是始终不变的，所以我觉得这是最重要的两个参数（当然其他参数也会有较大的影响），我发现q则会影响收敛的速率，q很小的时候，最后得到的曲线的波动会很小，但是数据要收敛好长的一段时间才稳定到最终值，如果q很大的话，收敛速度就比较快，但是最后可能还是存在些许的波动，其实就是导致滤波滤的不干净。最终因为我比较相信阻抗的值是不变的，所以我也觉得q应该取小一点，r是测量方差，这个好像比较容易可以用实验测到。最后的滤波效果可以这样：


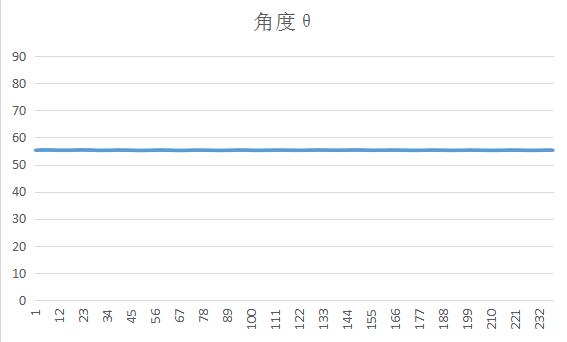
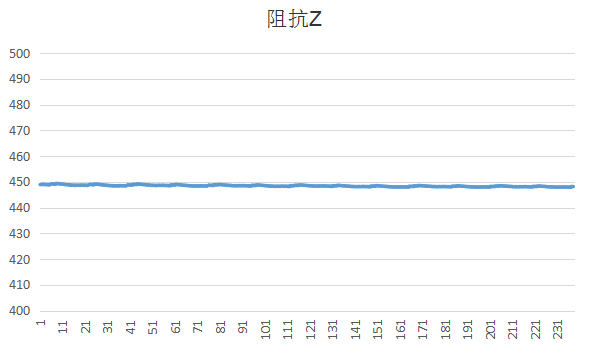
因为之前测量的数据都是从STM32读取然后用execl作图，为了方便其他量的观测还有调参，编写了个相应的matlab仿真程序。

MATLAB实现的简单卡尔曼滤波

其实matlab主要完成的是滤波还有画图比较，因为原始数据还是要从下位机读到。我把原始数据存到txt文本文件中，运行matlab代码可以实现卡尔曼滤波和画图，matlab的程序如下：

 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %start from the very beginning,and to create greatness
 %@author: LinChuangwei 
 %@E-mail：979951191@qq.com
 %@brief：卡尔曼滤波的小测试程序
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function lcw_kalman_plot
clear all
clc;
close all;
%打开一个文本文件，使用时将数据保存在一个*.txt文件里面
[fname, fpath] = uigetfile(...
    {'*.txt', '*.*'}, ...
    'Pick a file');

z = load(fullfile(fpath, fname));%加载所有的原始数据，matlab是从1开始的,这个值也就是测量值
lcw_length = length(z);%求长度

%分配内存
xlcw_ = zeros(1, lcw_length);%x的先验估计
xlcw = zeros(1, lcw_length);%x的后验估计
residual = zeros(1, lcw_length);%滤波残余
p_ = ones(1, lcw_length);%先验均方差
p = ones(1, lcw_length);%后验均方差
k = zeros(1, lcw_length);%卡尔曼增益
%几个初始化   
%状态模型: x(t) = a x(t-1) + w(t-1)
%测量模型: z(t) = h x(t) + v(t)
%初步猜测，这两个数是猜测的，对于卡尔曼滤波算法来说，这两个值是否准确并不十分重要
xlcw(1) = 40;%需要调
p(1) = 5e2;%需要调
A = 1;
H = 1;%h是激励倍数，实际工作中h可能会随着时间而变化，在这里假定为常标量,但是我们可以改
Q = 10e-4;%5e2;%这两个值的初始化就很关键了   噪声协方差  %需要调
R = 5e2;%10e-4;%需要调

%卡尔曼滤波
%进入循环过程。下面nsim为总循环次数
for t = 2 : lcw_length,
%预测
xlcw_(t) = A * xlcw(t-1);%x的先验估计由上一个时间点的后验估计值和输入信息给出，这里没有输入，b为0
residual(t) = z(t) - H * xlcw_(t);%z(t)的实际测量值和预测值之间的差为滤波过程的残余(革新)
p_(t) = A * A * p(t-1) + Q;%计算先验均方差
%校准
k(t) = H * p_(t)/(H * H * p_(t) + R);%k(t)为卡尔曼增益或卡尔曼混合系数
p(t) = p_(t) * (1 - H * k(t));%计算后验均方差
xlcw(t) = xlcw_(t) + k(t) * residual(t);%利用残余的信息改善对x(t)的估计，给出后验估计，这个值也就是输出
end

%下面开始绘图
t = 1: lcw_length;
%画出状态和状态估计
figure;
h1 = plot(t, xlcw_, 'b');
hold on
h2 = plot(t, xlcw, 'g');
h3 = plot(t, z, 'r');
xlabel('By LinChuangwei');
hold off
legend([h1(1) h2(1) h3(1)], '先验估计', '后验估计', '测量值');%显示格式
title('先验估计, 后验估计和测量值的比较');
ylabel('状态');
%axis(gca,[0,lcw_length,30,70]);%规定画图的范围

%画协方差
figure;
h1 = plot(t, p_, 'b');
hold on;
h2 = plot(t, p, 'g');
hold off
legend([h1(1) h2(1)], '先验估计', '后验估计');
title('先验估计和后验估计的协方差');
ylabel('协方差');
xlabel('By LinChuangwei');
%axis(gca,[0,lcw_length,0,500]);%规定画图的范围

%卡尔曼增益
figure;
h1 = plot(t, k, 'b');
legend([h1(1)], '卡尔曼增益');
title('卡尔曼增益');
ylabel('卡尔曼增益 k');
xlabel('By LinChuangwei');

运行时会要你打开一个存放着原始数据的文本文件，然后从文件中得到数据进行处理，选取一次数据，运行的结果如下：
先验估计，后验估计和测量值的比较

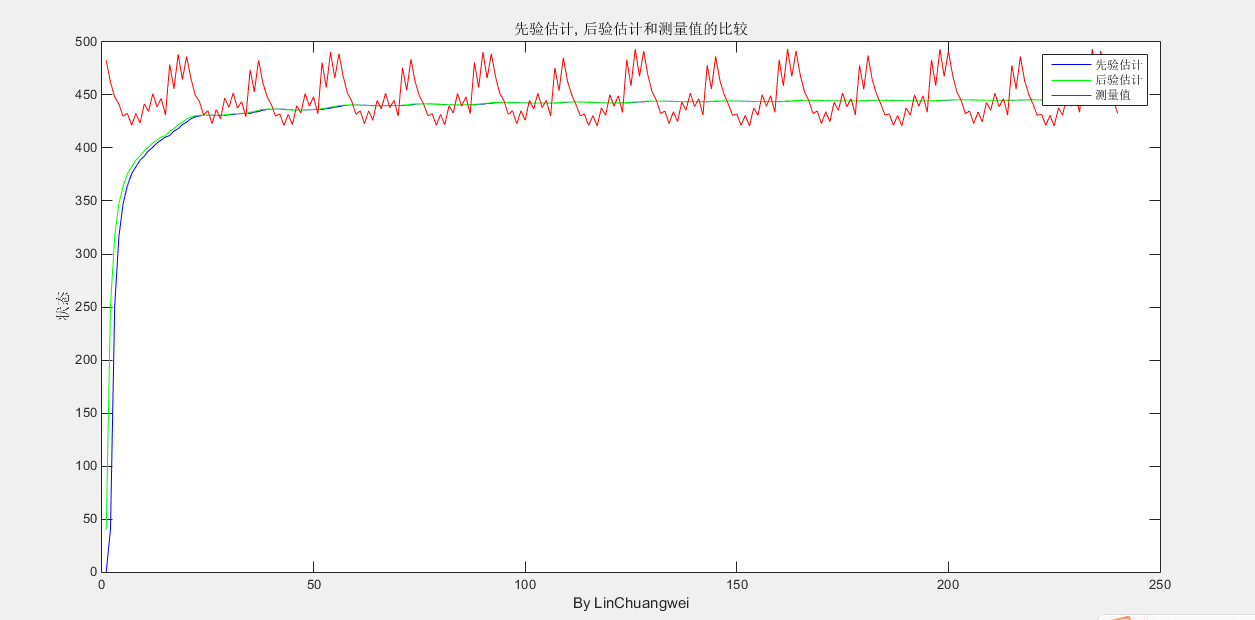
协方差，最开始那个500是自己设置的，可以设为别的（设置为别的之后曲线开始的点也就变了），这里只是为了说明它最终是会收敛于某个值

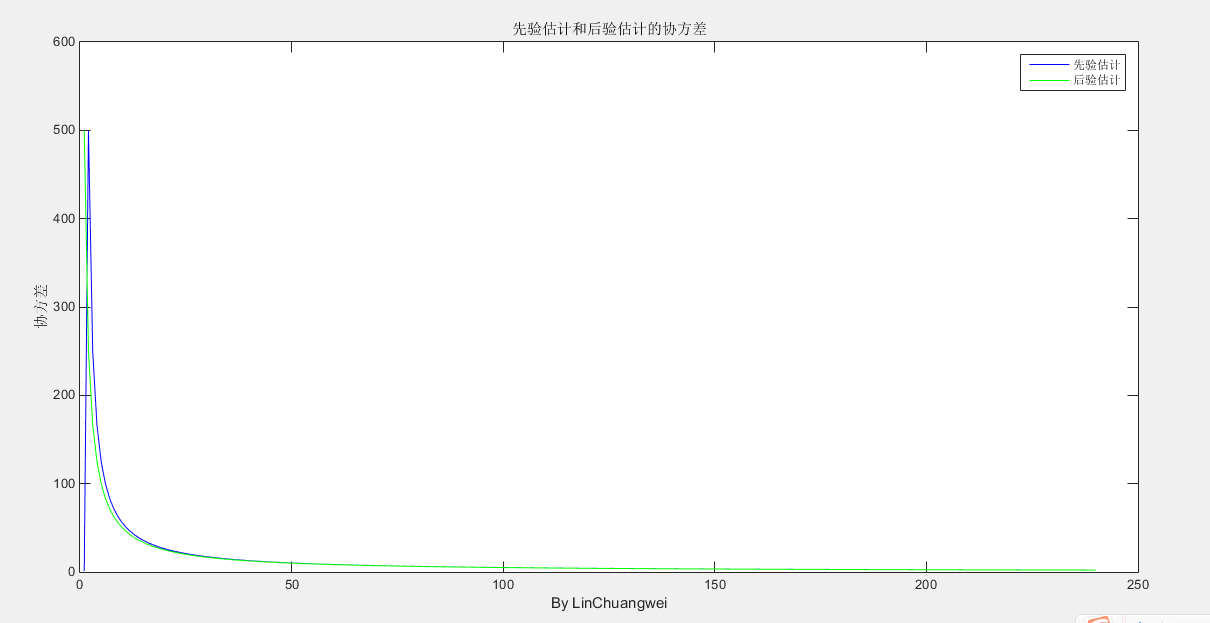
卡尔曼增益

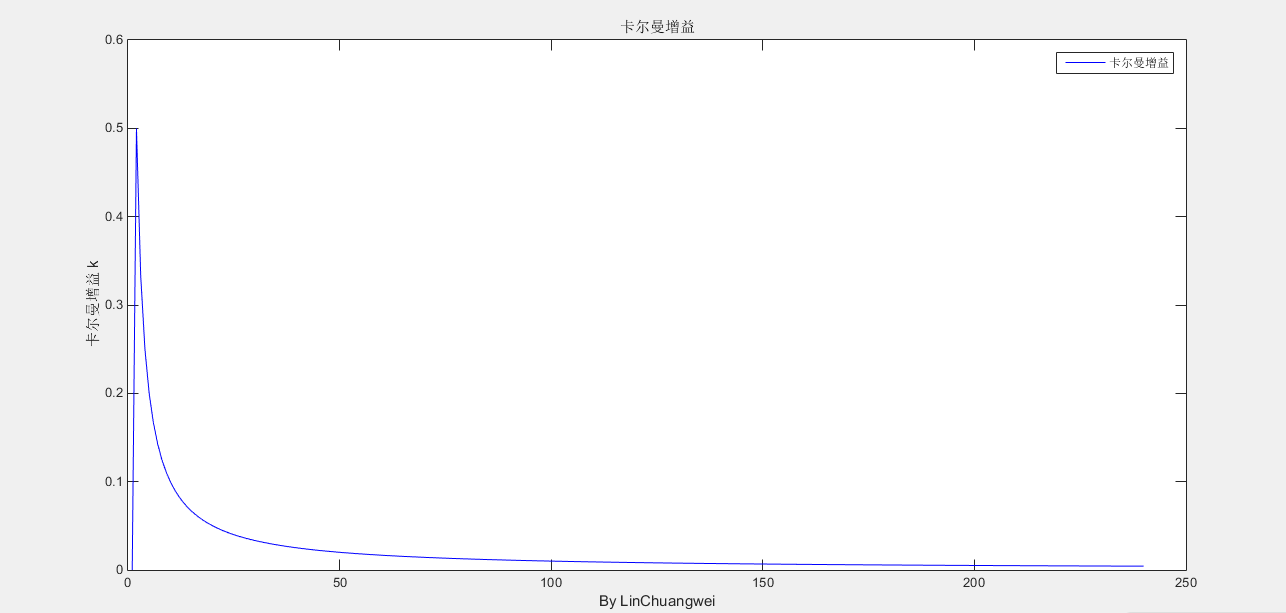
就算是另外的数据最终也是可以稳定的

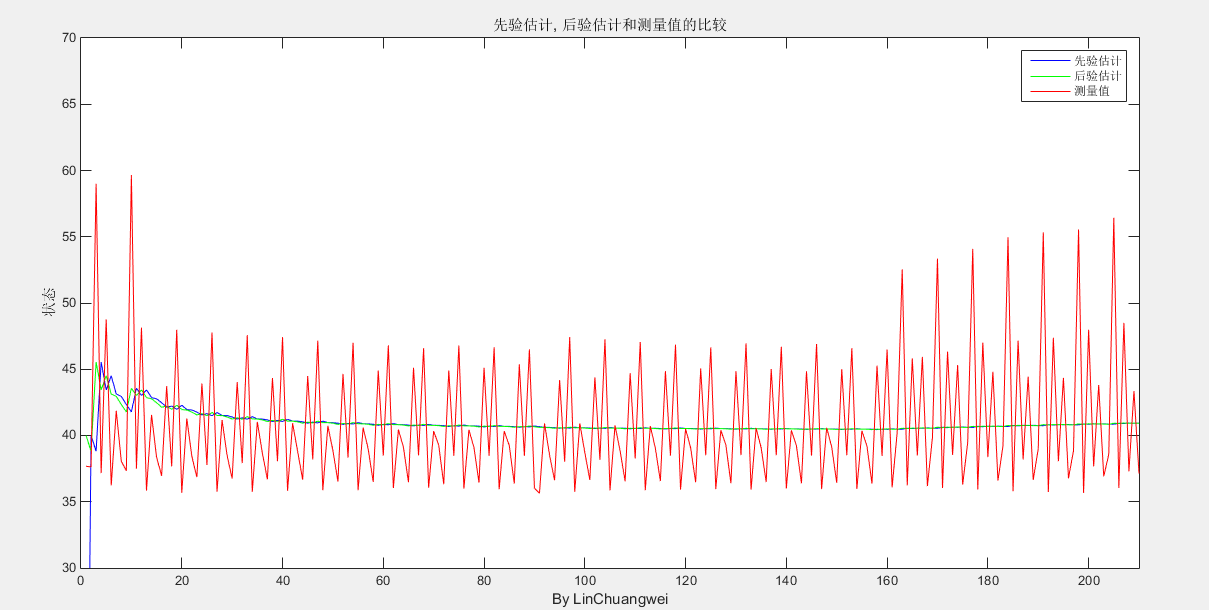
从其最开始的部分我们可以看到，曲线是慢慢收敛的，所以明智的做法应该是舍弃最开始的一段数据。或许有些人看图像觉得可能均值滤波的效果和这个差不多，但是使用均值滤波实际做的效果是这样的

远没有卡尔曼滤波的效果好。

卡尔曼滤波的数学推导

我本来觉得卡尔曼的数学推导应该会是比较难的，看了其标量的推导后觉得其实不复杂。因为这里要打公式好麻烦，我就直接从参考文献里面截取出来。

这里的先验估计表示为x^−,后验估计为x^,真实值为x

在先前测量值Z(t)和预测值之间的差就是残余

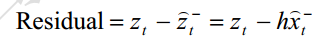
残余反映了预测值和实际值之间的差别。残余为零的话，估计值和实际值完全吻合。如果残余很小，表明估计值很好，反之就不好。卡尔曼滤波器可以利用残余的这一信息改善对X(t) 的估计，给出后验估计

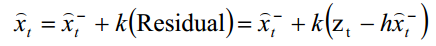
这里的k就是卡尔曼增益，现在剩下的问题就是如何找到 k 的值，使得估计为最优。为此需要定义先验均方差和后验均方差。
先验误差和后验误差分别定义为

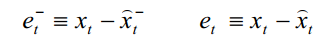
它们的方差就是先验均方差和后验均方差

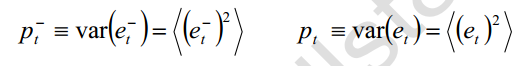
最优的 k 值是使后验均方差为最小的值，就是下式成立时的 k 值

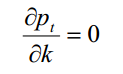
下面变成了求微分的过程。为此，先计算先验均方差

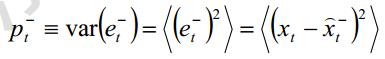
由上面最初的系统模型可得

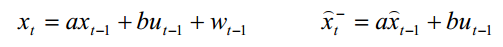
代入可以得到

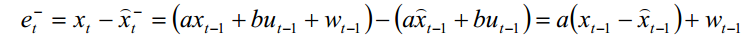
因此

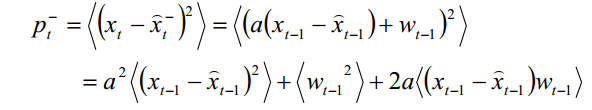
又X及其后验估计和高斯白噪声均是没有关联的，因此有

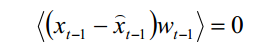
进而可得

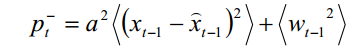
以及

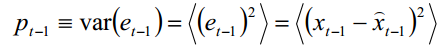
又因为高斯白噪声的方差为Q，所以

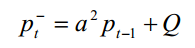
下面计算后验均方差
由先前给出的后验估计值的式子有

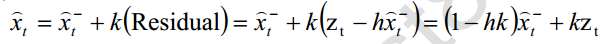
又卡尔曼的直接测量量如下

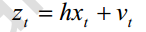
代入后验误差中

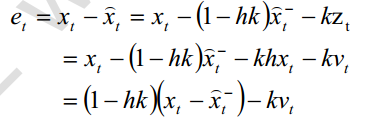
所以方差

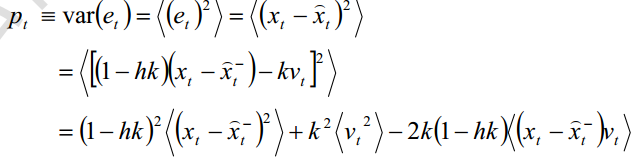
同理，真实值和先验估计和高斯白噪声没有关联，有

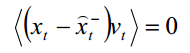
所以

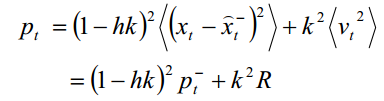
现在来计算k值，k 值应当是使后验均方差为最小的值。解下面的方程：

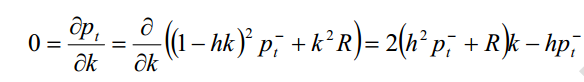
得到k值为

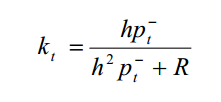
到这里就可以得到卡尔曼滤波器的5条公式了。
卡尔曼滤波的过程其实就是一直在进行如下的迭代

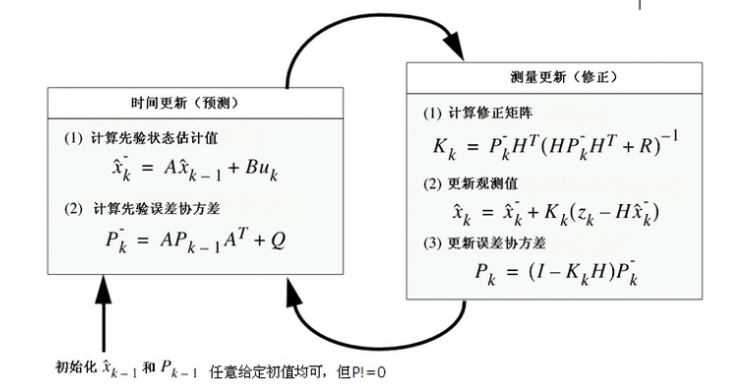
更详细的推导和细节，应用请参考其他的文献。
本文所有代码和测试数据都已经上传到我的github，希望各位提出建议和改进之处，谢谢！