机器学习的数据预处理
数据预处理是在机器学习算法开始训练之前对原始数据进行筛选,填充,去抖,类别处理,降维等操作;有的方法可以防止由于数据的原因导致的算法无法工作,有的方法可以加速机器学习算法的训练,提高算法的精度。
1.缺失数据的处理
1.1查看数据确缺失情况
举个例子说明如何查看数据缺失的情况:
import pandas as pd #创建一个缺失数据的DataFrame df = pd.DataFrame([\ [1,2,3,4],\ [5,6,None,8],\ [9,None,11,None,],\ [13,14,15,None,]\ ],\ columns=["A","B","C","D"]) lossDataCheck(df) #打印每列数据缺失的情况 print(df.isnull().sum())
运行结果是:
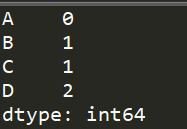
1.2.将存在缺失值的特征或样本删除
1.2.1按行删除
将包含空值的行全部删除使用DataFrame类里的dropna方法:
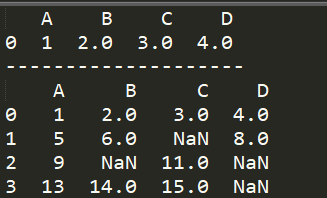
print(df.dropna()) print("-"*20) print(df)
结果如下所示,可知dropna方法并不对原数据进行修改。
1.2.2按列删除
删除包含空值的列也是dropna方法,不过需要给函数传个参数:
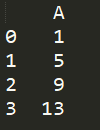
print(df.dropna(axis=1))
结果如下:
1.2.3按条件删除
只有当一行数据全空时才删除:
df.dropna(how="all")
当一行数据缺少达到某个阈值时才删除:
df.dropna(thresh=3)
指定的列里有数据缺失的行,才删除
df.dropna(subset=["A"])
更多删除操作请参考:dropna
1.3.缺失数据的填充
1.3.1 Imputer类
数据填充使用的是scikit-learn中的Impute类
最常用的技术之一是“均值插补”(meaneinputation)
from sklearn.preprocessing import Imputer imr = Imputer(missing_values="NaN",strategy="mean",axis=0) imr = imr.fit(df) imputed_data = imr.transform(df.values)
print(imputed_data)
结果:

如果把axis设置为1.则是使用行数据的均值进行填充;
strategy策略可选的有:中位数(“median”),最常出现的值(“most_frequent”)。
1.3.2 pandas自带方法
avg_mean = df["D"].mean() df["D"] = df["D"].fillna(avg_mean)
这种方法需要自己一列一列去操作。
2.数据去抖
工业界中的过程数据可能会由于偶然误差出现几个特别不符合实际的数据,对数据做去抖其实就是删除那些明显是偶然误差的数据。
有两种方法去抖:
1)非常了解该数据的特性,比如常规的上限下限值,那么可以通过这些条件取出样本中异样的数据;
2)假定数据符合正态分布,那么仅保留大概率下的数据,对于那些分布在下概率下的数据进行丢弃处理。
2.1通过自定义条件筛选
特征数据的上下限筛选,假定temperature代表工厂温度,工厂温度几乎不可能低于35,也不太可能高于60,那么通过条件筛选出正常的数据如下
import pandas as pd data = pd.DataFrame([\ [1,55],\ [2,45],\ [3,43], [2,44], [2,63],\ [3,33]\ ],columns=["working_num","temperature"]) data_screen = data[(data.temperature>35)&(data.temperature<60)] print(data_screen)
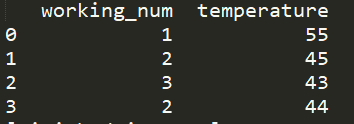
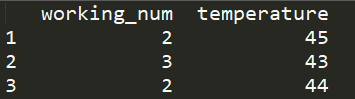
data_screen = data[(data.temperature>35)&(data.temperature<60)&(data.working_num>1)] print(data_screen)
也可加多个条件筛选,如上,得出的结果是:
2.2根据正态分布除去小概率事件数据
假设样本中的特征数据符合正态分布,那么依据正态分布的条件可知在$(u\pm 3\sigma)$区间取值的概率为99.73%,而在区间之外的取值概率不到0.3%,可以认为是极小概率事件;$(u\pm 2\sigma)$区间之外的概率为85.45%。
使用正常的数据更容易得出合适的模型,所以筛出小概率事件的数据有时可以帮助我们提升算法的性能。
我们可以子集实现一个筛出小概率事件数据的函数:
import numpy as np import pandas as pd def shiftOutExtreme(data,column,ratio=3): ''' 输入: data:DataFrame 样本数据集 colum:str 选中的列名 ratio:float/int 系数,此值越大,取值空间越大 输出: DataFrame 新的数据集 ''' my_array = data[column].values c_mean = np.mean(my_array) c_std = np.std(my_array) print(c_mean,c_std) new_data = data[(data[column] < ratio*c_std + c_mean) & (data[column] > c_mean - ratio*c_std)] print(new_data) return new_data data = pd.DataFrame([\ [1,13.1],\ [1,12.8],\ [1,13.2], [1,12.9], [1,12.7],\ [1,8.8]\ ],columns=["working_num","temperature"]) shiftOutExtreme(data,"temperature",1)
结果将最后一个8.8的数据筛选出去了:

3.数据类别处理
类别型数据是针对数值型数据而言的,因为算法没法处理类别型数据,例如颜色数据等等。在机器学习中可以将数据分为3大类型:
1)数值型数据:可以直接进行数学运算的数据;
2)有序数据:类别的值可以进行排序,例如衣服的XL,L,M号码等;
3)标称数据:不具备排序的特性,例如颜色数据等。
这里主要对有序型数据和标称数据进行处理。
3.1有序型数据的处理
类似于SQL中的外键映射,有序型数据也可通过映射转换为数值型的数据。
例如下面的例子:
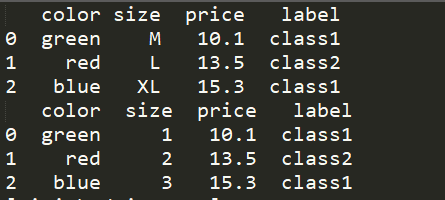
import pandas as pd df = pd.DataFrame([\ ["green","M",10.1,"class1"],\ ["red","L",13.5,"class2"],\ ["blue","XL",15.3,"class1"]\ ],columns=["color","size","price","label"]) print(df) size_mapping = {"M":1,"L":2,"XL":3} df["size"] = df["size"].map(size_mapping) print(df)
结果如下:
3.2 类标编码
类标一般是string类型的,但有些机器学习库要求类标以数值形式进行编码;可以同有序数据编码方式一样,通过映射将类标映射到数值列表上,不过由于类标是无序的,映射后的数值大小没有意义,仅仅是一种映射而已。
label_mapping = {label_name:idx for idx,label_name in enumerate(np.unique(df["label"]))}
df["label"] = df["label"].map(label_mapping)
print(df)
结果是:

此外scikit-learn中的LabelEncoder类可以很方便的完成类标的编码工作:
from sklearn.preprocessing import LabelEncoder class_le = LabelEncoder() #将类标编码 y = class_le.fit_transform(df["label"].values) #将类标还原 class_le.inverse_transform(y)
3.3标称特征上的独热编码(one-hot encoding)
独热编码技术:创建一个新的虚拟特征,虚拟特征的每一列代表标称数据的一个值,例如颜色可以虚拟出基础的红绿蓝三色,所有颜色都可以通过这3个颜色的配比调和出来。
pandas模块中的get_dummies方法可以很方便的实现独热编码,此方法只对字符串列进行转换,其他列保持不变。
new_df = pd.get_dummies(df) print(new_df)
结果如下:

4.数据集划分
4.1 现有模块的方法
使用scikit-learn.model_selection 模块中的train_test_split方法对数据集进行划分时,需要先子集把特征列和类标列分开,并子集给定划分的比例。
from sklearn.model_selection import train_test_split df = pd.DataFrame([\ ["green","M",10.1,"class1"],\ ["red","L",13.5,"class2"],\ ["blue","XL",15.3,"class1"]\ ],columns=["color","size","price","label"]) X,y = df.iloc[:,:-1].values,df.iloc[:,-1].values X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
其中test_size是划分数据集时测试数据所占全部数据的比例。
4.2 使用python自己实现
def train_test_split(X,y,test_size,random_state=False): #判断数据长度是否相等 if len(X) != len(y): raise KeyError("X,y have difference num") length = len(X) if random_state: new_sequence = np.random.permutation(range(length)) X,y = X[new_sequence],y[new_sequence] test_num = int(length * test_size) return X[test_num:],y[test_num:],X[:test_num],y[:test_num]
5.特征缩放
使用梯度下降法的算法中,大多要使用特征缩放;
将不同的特征缩放到相同的区间,目前常用的技术有:
1)归一化:将特征缩放到区间[0,1],技术上是:$x_{norm}^{(i)}=\frac{x^{(i)}-x_{min}}{x_{max}-x_{min}}$;其中max,min分别代表特征数据中的最大最小值;
2)标准化:将特征数据缩放为均值为0,方差为1的的正态分布数据,技术上:$x_{std}^{(i)}=\frac{x^{(i)}-u_{x}}{\sigma _{x}}$,其中u代表特征数据平均值,$\sigma$表示特征数均的标准差。
5.1归一化(normalization)实现
使用scikit-learn.preprocessing库中的MinMaxScaler类
from sklearn.preprocessing import MinMaxScaler mms = MinMaxScaler() X_train = mms.fit_transform(X_train) X_test = mms.tansform(X_test)
必须仅使用训练集进行归一化训练,测试集不可参与归一化类的训练(即fit),之后在训练好的归一化类对象上进行转换;程序也可以这么写:
from sklearn.preprocessing import MinMaxScaler mms = MinMaxScaler() mms.fit(X_train) X_train = mms.transform(X_train) X_test = mms.tansform(X_test)
5.2标准化(standardization)实现
使用scikit-learn.preprocessing库中的StandardScaler类
使用方式同归一化类相同。
6.数据降维
数据降维可以减少模型的复杂度,降低过拟合风险,同时通过降维可以提高模型训练以及运算速度,提高算法性能。
数据降维这边主要划分为被动降维与主动降维两大部分;其中被动降维是指通过L1正则化生成模型参数的稀疏矩阵,被动的使多个特征的模型参数为0;主动降维是指通过降维技术,降低原始数据集的特征数量。
6.1被动降维(L1正则化)
其实不属于数据预处理的部分,不过能实现数据降维,这里也简单提一下。
L1正则化:在算法的代价函数中加上L1正则化函数,函数表达式为$L1:\left \| w \right \|_{1}=\sum_{j=1}^{m}\left | w_{j} \right |$。
L1正则化意在惩罚过多过大的参数,所以在代价函数里,L1正则化函数前的系数越大,则其惩罚力度越大,一些无关紧要的特征对应的模型参数就越可能为0.
6.2主动降维
主动降维技术分为2个大类:
1)特征选择:在原数据集特征上选出其子集,不对特征本身进行其他的构造,仅丢弃不重要的特征;
2)特征提取:对原数据集特征进行推演,构造一个新的特征集。
6.2.1 特征选择:
一个经典的序列特征选择算法是“序列后向选择算法”(SBS),假定要将一个拥有d个特征的数据集降低到k维,SBS的步骤如下:
1)定义衡量标准函数J作为判定函数,算法的目标是最大化J;
2)检查目前特征个数是否为k,如果是,则终止算法,返回新的数据集;
3)否则计算每个特征的衡量函数J,选择最大的J对应的那个特征进行删除,并跳转第2)步。
一般J都选择性能损失函数,即删除一个特征后模型性能损失的值,假设A为整个特征集,$pfm(A)$为以特征集A训练后的模型的性能;$A_{i}$表示A特征集中的第i个特征,$pfm(A-A_{i})$为删除第i个特征后的模型的性能,那么:
$J(A_{i})=pfm(A) - pfm(A-A_{i})$
不要此类方法只适合于特征之间相关性不大的情况。
还有之前在随机森林里提到的信息熵也可以作为特征选择的一个参考方向。
6.2.2特征提取
是一种将原始数据集变换到一个维度更低的新的特征子空间的一门技术。
内容太多,重开一篇随笔记录。


