支持向量机(SVM)
算法分类:监督算法,分类算法
1.SVM算法简介
SVM是分类算法中比较特殊的一种,它并不像LR算法那样使用到所有数据进行模型训练,SVM虽然也使用了全部数据,但是绝大部分数据只参与约束条件的限制,不参与最终模型参数的训练。SVM的目标是分类最大化分类间隔,何为最大化分类间隔,将在下面的内容解释。
涉及到的名词有:分割超平面,决策边界,分类间隔,支持向量(support vector)
了解这几个名词即了解了SVM算法的构建思路。
1.1分割超平面
在分类问题中,通过模型对数据类别进行预测,线性模型是通过线性函数$w^{T}x + b$来预测数据的类别,在坐标图中$w^{T}x + b=0$这个平面(线)将数据分为两部分,每一部分代表一种类别;这里的$w^{T}x + b=0$平面即分割超平面。
值得注意的是分割超平面不一定只有一个,如下图,分割超平面其实可以有无数个:
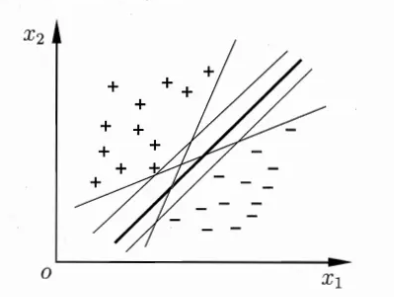
1.2决策边界
将分割超平面沿着其垂直线的方向平移,当接触到第一个数据时停止,此时会得到两个停止的超平面,这两个超平面即模型的决策边界。
下图中两个虚线即分割超平面向两个方向平移后得到的决策边界。
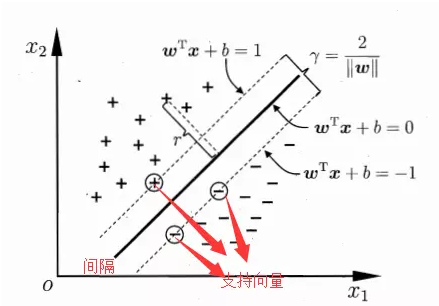
1.3分类间隔
分类间隔即决策边界两个平面之间的距离。
1.4支持向量
是数据集中最接近分割超平面的数据,支持向量是分割超平面向两边移动的时候最先触碰到的几个数据点,正分类那一边最接近分割超平面的称为正支持向量,分类为负的你那一边最接近分割超平面的数据称为负支持向量。
1.5SVM目标
SVM算法的目标是:在保证分类正确的基础上,最大化分类间隔。
最终结论就是:SVM算法就是在满足正确分类条件下,找到分类间隔最大的分割超平面。
2.分类正确与分类间隔
假设(w,b)参数的线性函数能够正确的对数据进行分类,即对样本数据中$y^{(i)}=1$时$w^{T}x^{(i)}+b>0$,而对$y^{(i)}=-1$时$w^{T}x^{(i)}+b<0$。
使用决策边界的思维,我们不将0作为分类的临界点,而是将±1作为分类的临界点,则有:
$y^{(i)}(w^{T}x+b)\geq 1\\$
可知正决策边界上的$w^{T}x+b$的值为1,负决策边界上的$w^{T}x+b$值为-1,所以根据距离公式可以得出决策边界之间的距离即:
$\frac{2}{\left \| w \right \|}\\$
SVM算法就是在满足正确分类条件下,找到分类间隔最大的分割超平面这句话用数学表示即为:
$max \frac{2}{\left \| w \right \|}
\\
s.t.\, \, \, y^{(i)}(w^{T}x+b)\geq 1,i=1,2,\cdots n \\$
等同于
$min \frac{1}{2}\left \| w \right \|^{2}$
$s.t.\, \, \, y^{(i)}(w^{T}x+b)\geq 1,i=1,2,\cdots n \\$
上面即SVM算法的基本型;这里就解释清楚了之前提到的SVM算法训练并未使用所有的训练数据,实际上只是用了支持向量,剩下的其他训练数据只要满足约束条件就可以了,并不参与到模型的参数训练。
3.求解带约束的优化问题
求解带约束的优化问题是SVM中比较难的部分,有约束的优化算法这篇博文介绍的比较详细;
SVM算法有5篇博文专门详细解释了SVM算法的推导部分,不过比较难,涉及到较多数学知识。
4.软间隔
前面的讨论中一直假定原始数据时线性可分的,实际问题中更多的是无法完美线性可分的,故需要允许SVM在一些样本上出错,由此引入软间隔概念。
软间隔也可以消除一些极端数据引起的过拟合问题。
软间隔引入了松弛变量这个概念,即放宽了对算法的约束条件,公式表达如下:
$w^{T}x^{(i)}\geqslant 1\, \, if\, \, y^{(i)}=1-\xi ^{(i)}$
$w^{T}x^{(i)}< -1\, \, if\, \, y^{(i)}=-1+\xi ^{(i)}$
由此,新的目标函数最小化公式如下:
$\frac{1}{2}\left \| w \right \|^{2}+C(\sum \xi ^{(i)})$
通过变量C,可以控制对错误分类的处罚力度,C较大时,分类出错会有很大的惩罚,C较小时,更加容易容忍分类错误。
使用scikit-learn库中提供的类可以很方便的实现SVM算法:
from sklearn.svm import SVC svm = SVC(kernal="linear",C=1.0,random_state=0) svm.fit(X_train,y_train)



