转导推理——Transductive Learning
在统计学习中,转导推理(Transductive Inference)是一种通过观察特定的训练样本,进而预测特定的测试样本的方法。另一方面,归纳推理(Induction Inference)先从训练样本中学习得到通过的规则,再利用规则判断测试样本。然而有些转导推理的预测无法由归纳推理获得,这是因为转导推理在不同的测试集上会产生相互不一致的预测,这也是最令转导推理的学者感兴趣的地方。
归纳推理中的一个经典方法是贝叶斯决策,通过求解P(Y|X)=P(X|Y)P(Y)/P(X)得到从样本X到类别Y的概率分布P(Y|X),进而使用P(Y|X)预测测试样本的类别。这一过程的缺点在于,在预测某一测试样本的类别之前,先要建立一个更通用的判别模型。那么是否能够更直接判别测试样本的类别呢?一个办法就是通过转导推理。转导推理由Vladimir Naumovich Vapnik(弗拉基米尔·万普尼克)于20世纪90年代最先提出,其目的就在于建立一个更适用于问题域的模型,而非一个更通用的模型。这方面的经典算法有最近邻(K Nearest Neighbour)和支持向量机(Support Vector Machine)等。
特别是当训练样本非常少,而测试样本非常多时,使用归纳推理得到的类别判别模型的性能很差,转导推理能利用无标注的测试样本的信息发现聚簇,进而更有效地分类。而这正是只使用训练样本推导模型的归纳推理所无法做到的。一些学者将这些方法归类于半监督模型(Semi-Supervised Learning),但Vapnik认为是转导推理3。这方面的经典算法有转导支持向量机(Transductive Support Vector Machine)等。
转导推理的产生的第三个动机在于模型近似。在某些工程应用中,严格的推导所产生的计算量可能是非常巨大的,工程人员希望找到某些近似模型能适应他们所面临的特定问题,不需要适用于所有情况。
如下图所示。判别模型的任务是预测未标注数据点的类别。归纳推理方法通过训练一个监督学习模型来预测所有未标注点的类别。这样,训练样本中就只有5个点供以训练监督学习模型。对于图中较靠中心的某点(红色圆圈),利用最近邻算法就会将其标记为A或C,但从所有数据组成的类簇来看,此点应标为B。
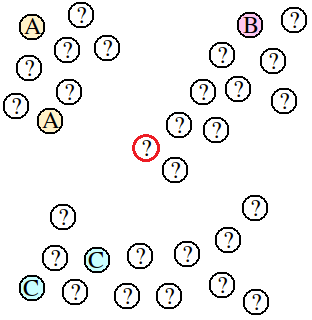
图1:少量标注样本时,使用KNN算法预测样本类别。训练样本是少量已经标注(A、B、C)的点,而其它大部分的点都是未标注的(记为?)。
转导推理会利用所有点的信息进行预测,也就是说转导推理会根据数据所从属的类簇进行类别标注。这样中间红色圈的点由于非常接近标为B的点所从属的类簇,就会标注为B。可以看出转导推理的优势就在于其能通过少量的标注样本进行预测。而其不足之处就在于其没有预测模型。当新未知点加入数据集时,转导推理可能需要与数据量成正比的计算来预测类别,特别是当新数据不断地被获取和加入时,这种计算量的增长显得犹为突出,而且新数据的添加可能会造成旧数据类别的改变(根据实际应用的不同,可能是好的,也可能是坏的)。相反地,归纳推理由于有模型存在,在计算量上可能会优于转导推理(模型的更新可能增加计算量)。
文章的后面部分将以二分类为例,先从较简单的情况开始,即给定大量的标注样本,判断测试样本的类别,讨论最近邻(k Nearest Neighbours,KNN)和支持向量机(Support Vector Machine,SVM)。接着就讨论在给定少量标注样本和大量测试样本的情况下,判断测试样本的方法,主要是转导支持向量机(Transductive Support Vector Machine,TSVM)。
最近邻与支持向量机
最近邻算法是通过考虑与测试样本最近的几个训练样本的信息来分类测试样本。最近邻算法的关键有二:
- 如何度量测试样本到训练样本的距离(或者相似度)
- 如何利用近邻的类别等信息
一种简单的办法是度量测试样本到训练样本间的距离,选择最近的若干个训练样本,若某一类别的点占多数,就简单地将测试样本归为那类。如下图所示,使用了欧几里得距离和街区距离度量测试样本到训练样本的距离。
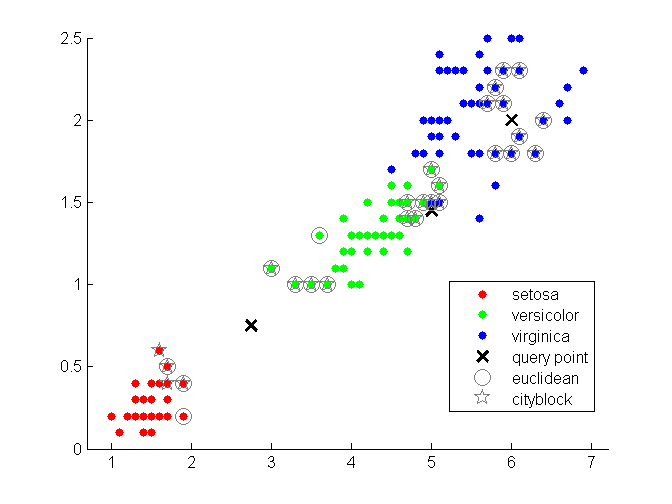
图2:最近邻示意图。使用欧几里得距离和街区距离进行度量
可以发现最近邻算法在预测每个测试样本的类别时,所利用的只是整个训练样本集中一部分。最近邻算法没有在训练样本集上归纳出一个通用的模型,而是只通过测试样本相近的点作判断。接着再来看看支持向量机又是如何从训练样本转导出分类面。
对于二分类问题,给定一个训练样本$(x_i,y_i)$,x是特征,y是类别标签(正类为1,负类为-1),i表示第i个样本。定义划分二类数据的分类面为$w^T x+b$,其中w为分类面的法向量,b为分类面的偏移量。正类在分类面的上方($w^T x+b$),负类在分类面的下方($w^T x+b$)。定义单个训练样本的函数间隔:$$\gamma_i = y_i(w^Tx_i+b)=|w^T x+b|$$
可以看出来,当$y_i$=-1时,训练样本是负类,$w^T x+b<0$,$\gamma_i$大于0,反之亦然。良好的分类面应能使训练样本的函数间隔最大。函数间隔不仅代表了特征被判别为正类或反类的确信度,而且是评价分类面的指标。如果同时加大w和b,比如在前面乘个系数(比如2),那么所有点的函数间隔都会增大二倍,这个对求解$w^T x+b=0$是无影响的。这样,为了限制w和b,可能需要加入归一化条件,毕竟求解的目标是确定唯一一个w和b,而不是多组线性相关的向量。故单个训练样本的函数间隔亦可写为: $$\gamma_i = y_i \left( \left(\frac{w}{\|w \| } \right)^T x_i + \frac{b}{\| w \|} \right)$$ 函数间隔亦可从几何间隔上推导得到。
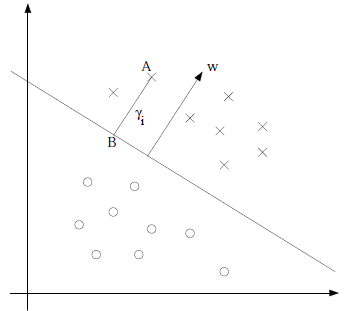
图3:以“×”标记的点是正类数据,以“O”标记的点是负类数据。A点位于分类面之上,B在分类面上,w是分类面的法向量。
设A点为$\left(x_i, y_i \right)$,w方向的单位向量为$\frac{w}{\Vert w \Vert}$,则B点横坐标$x=x_i-\gamma_i \frac{w}{\Vert w \Vert}$,代入B点所处的分类面方程:
$$\begin{align} w^Tx + b &= 0 \\ w^T \left( x_i - \gamma \frac{w}{\| w \|} \right) + b &= 0 \\ \gamma \frac{w^T w}{\| w \|} &= w^T x +b \\ \gamma_i &= \frac{w^T x + b}{\| w \|} = \left( \frac{w}{\| w \|} \right)^T x +\frac{b}{\| w \|} \end{align}$$
与函数间隔的归一化结果是一致的。根据转导推理的原理,我们大可不必使所有训练样本到分类面的函数间隔最大,只需让离分类面比较近点能有更大间距即可。也就是说求得的超平面并不以最大化所有点到其的函数间隔为目标,而是以离它最近的点具有最大间隔为目标。 定义训练样本集(m个样本)上的函数间隔: $$\gamma_i = \max \limits_{i-1,\dots,m} \gamma_i$$ 也就是训练样本集上离分类面最近的样本点到分类面的距离。求解模型形式化定义如下: $$\begin{align} \max \limits_{w,b}& \gamma \\ s.t.& y_i \left( w^Tx +b \right) \ge \gamma ,\; i = 1,\dots,m \\ &\| w \| =1 \end{align}$$ 由于$\Vert w \Vert = 1$,此最大化函数不是凸函数,没法直接代入Matlab等优化软件进行计算。注意到几何间隔和函数间隔的关系,令 $$\hat{\gamma} = \frac{\gamma}{\| w \|} = \frac{1}{\| w \|}, \; \gamma = 1$$ 这里除以$\Vert w \Vert$是为了使求出w和b的确定值,而不是w和b的一组倍数。$\gamma = 1$的意义是使得训练样本集上的函数间隔为1,也即是将离超平面最近的点的距离定义为$\frac{1}{\Vert w \Vert}$。而其最大值,也就是的$\frac{1}{2} \Vert w \Vert^2 $最小值,则原最大化函数可改写为: $$\begin{align} \max \limits_{w,b}& \frac{1}{2} \Vert w \Vert^2 \\ s.t.& y_i \left( w^Tx +b \right) \ge 1 ,\; i = 1,\dots,m \ \end{align}$$ 以上讨论适用于二类可分的情况,当两类不可分时,引入松驰变量$\xi_i$替代$\gamma$ $$\xi_i = \max\left( 0, \gamma-y_i \left( \langle w,x_i \rangle + b \right) \right)$$ 最终的求解将使用分类面的对偶表达及相关泛函,但这不是本文的重点。KNN和SVM的分类效果如下图所示:
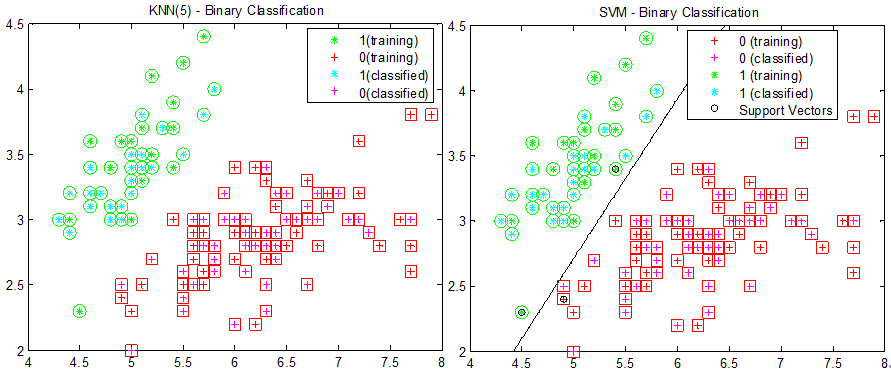
图4:KNN(选择5个最近邻)和SVM的分类结果,数据使用Matlab的Fisher Iris的一维和二维数据
在标注样本充足的情况,最近邻和支持向量机都表现得不错。但当标注样本不足时,最近邻和支持向量机的表现就显著下降。如下图所示。
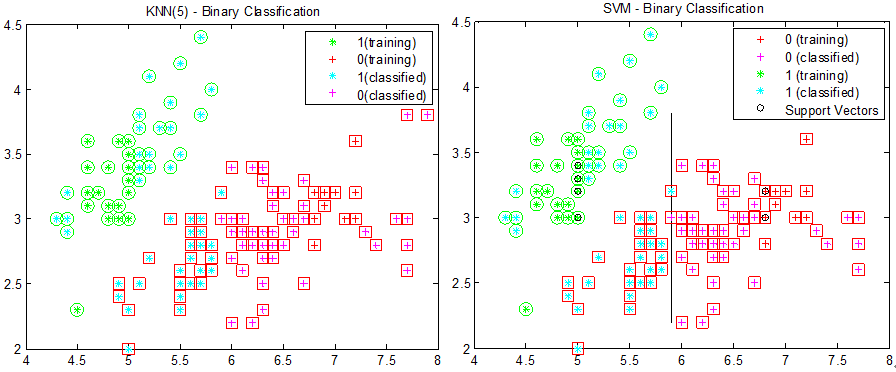
图5:标注数据只取x坐标值在[4.5 5]和[7 7.5]之间的点时,KNN和SVM的分类结果
观察分类结果可以看到,因为训练样本的x坐标只在某一区间,选取的支持向量使得分类面几乎与y轴平行。如果能使得分类方法“看到”两类数据(包括训练样本和测试样本)的分布,那是否就能得到一个较好的分类面了呢?
转导支持向量机
当训练数据和测试数据在训练模型时都可被使用时,如何才能使分类算法更加有效呢?形式化地说明,在给定训练数据 $$\left( x_i, y_i \right), \dots, \left( x_l, y_l \right) \; y \in \left(1 , -1\right)$$ 和测试数据 $$x_1^*, \dots , x_k^*$$ 的条件下,在线性函数集$ y = ( w \centerdot x ) + b$中找到一个函数,它在测试集上最小化错误数。在数据是可分的情况下,可以证明通过提供测试数据的一个分类结果 $$ y_1^*, \dots , y_k^* $$ 使得训练数据和测试数据 $$\left(x_1, y_1 \right), \dots, \left(x_l, y_l \right), \left(x_1^*, y_1^* \right), \dots , \left(x_k^*, y_k^* \right) $$ 可以被最优超平面以最大间隔分开。也就是说我们的目标是找到最优超平面 $$ y = \left( w^* \centerdot x \right) + b $$ 使得$\frac{1}{2} \Vert w \Vert^2$最小,且满足 $$\begin{align} y_i \left[ \left( w^* \centerdot x_i \right) + b \right] &\geq 1 , \; i = 1,\dots,l \\ y_j \left[ \left( w^* \centerdot x_j^* \right) + b \right] &\geq 1 , \; j = 1,\dots,k \\ \end{align}$$ 当数据不可分时,在不等式中加入松驰变量。即在满足 $$\begin{align} y_i \left[ \left( w^* \centerdot x_i \right) + b \right] &\geq 1 - \xi_i , \; \xi_j \ge 0, i = 1,\dots,l \\ y_j \left[ \left( w^* \centerdot x_j^* \right) + b \right] &\geq 1 - \xi_j , \; \xi_j \ge 0, j = 1,\dots,k \\ \end{align}$$ 的情况下,使得$\frac{1}{2} \Vert w \Vert^2 + C\sum_{i=1}^l \xi_i + C^*\sum_{j=1}^k \xi_j$最小。如下图所示。
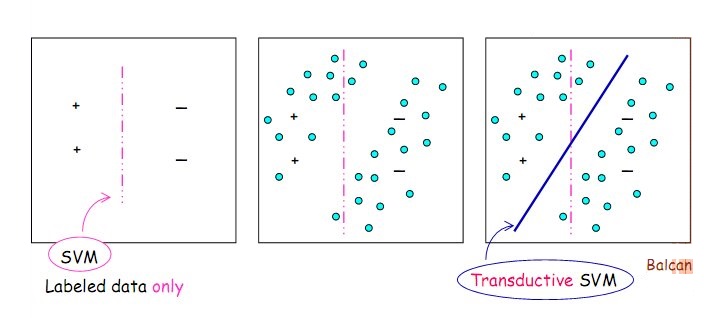
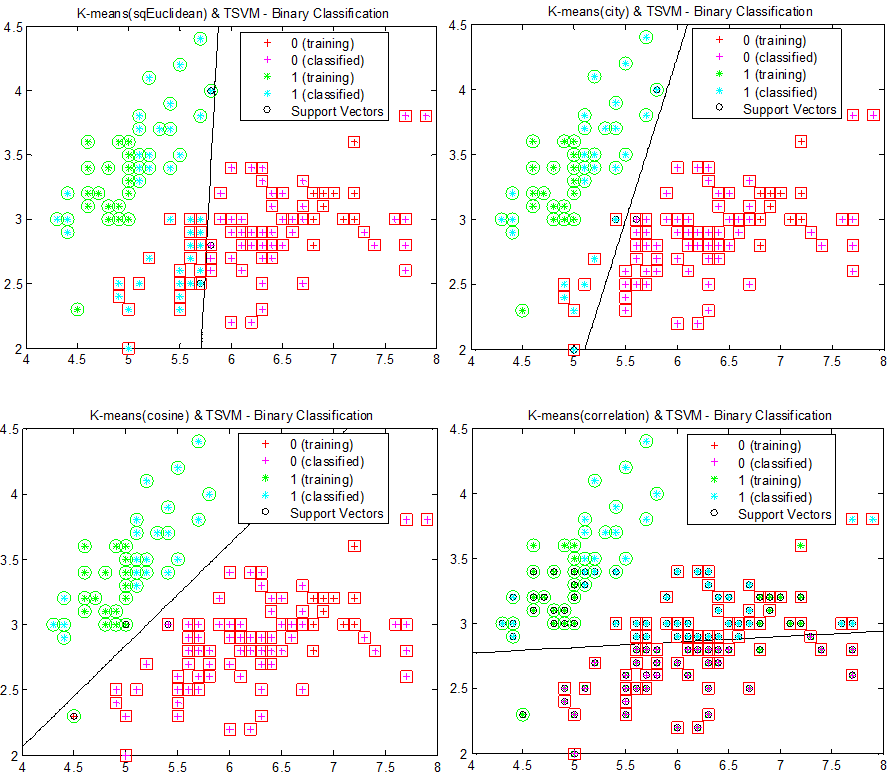
图6:标注数据以“+”和“-”标记,以青色填充的圆圈表示未标注数据。红色虚线代表分类面,左边和中间的分类面由SVM产生,右边的分类面由TSVM产生。 求解上述问题,实际上是针对固定的$y_1^*, \dots, y_k^*$找出最优超平面的对偶表达: $$f\left( x \right) = sign \left[ \sum_{i=1}^{l}\alpha_i y_i K\left(x, x_i \right) + \sum_{j=1}^{k} \alpha_j^* y_j ^* K\left(x, x_j^* \right) + b \right]$$ 为此必须使得泛函 $$\begin{align} W \left( y_1^*,\dots,y_k^* \right) &= \max\limits_{\alpha, \alpha^*} \Bigg\{ \sum_{i=1}^l \alpha_i + \sum_{j=1}^{k} \alpha_j^* \\ &- \frac{1}{2} \bigg[ \sum_{i,r=1}^{l} y_i y_r \alpha_i \alpha_r K\left(x_i, x_r \right) + \sum_{j,r=1}^{k} y_j^* y_r^* \alpha_j^* \alpha_r^* K\left(x_j^*, x_r^* \right) \\ &+ 2\sum_{j}^{k}\sum_{r=1}^{l} y_j y_r^* \alpha_j \alpha_r^* K\left(x_j, x_r^* \right) \bigg] \Bigg\} \end{align}$$ 在满足约束 $$\begin{align} 0 &\leq \alpha_i \leq C \\ 0 &\leq \alpha_j^* \leq C^* \\ \sum_{i=1}^{l} y_i \alpha_i &+ \sum_{j=1}^ky_j^*\alpha_j^* = 0 \end{align}$$ 的条件下达到它的最小值。一般而言,这一最小最大问题的精确解需要搜索测试集上所有的$2^k$种分类结果。对于少量的测试样本(比如3~7),这一过程是可以完成的。但对于大量的测试样本,可以使用各种启发式过程,例如先通过聚类测试数据将测试数据暂分类,再应用SVM划分各类的分类面。如下图所示。
图7:首先对图5的数据进行K-means聚类,接着对两个类使用SVM进行划分分类面。为了比对不同距离对分类的影响,从左至右,从上至下,使用欧几里得距离、街区距离、余弦距离和相关距离(1-相关系数,公式见下)进行K-means聚类。圆形和正方形表示正确的分类。
设数据点x有n个特征,即n维,则任意两个数据点$x_s$,$x_t$的相关距离$d_st$为 $$\begin{align} d_st = 1 - \frac{ \left( x_s - \overline{x_s} \right) \left( x_t - \overline{x_t} \right)^{'} }{ \sqrt{\left( x_s - \overline{x_s} \right) \left( x_s - \overline{x_s} \right)^{'}} \sqrt{\left( x_t - \overline{x_t} \right) \left( x_t - \overline{x_t} \right)^{'}} } \end{align}$$ 图中先对数据点进行聚类,再对聚成的两类做SVM分类。显然这一做法对聚类得到的类簇很敏感。使用余弦距离时,分类效果最好,这其中很大一部分原因就在于使用余弦距离进行K-means聚类后,两类已经被很好地分开了,再使用SVM显然能达到更好地结果。为了降低聚类对之后分类的影响,可以在类簇中随机抽取某些样本作为训练样本,结果如下图所示:
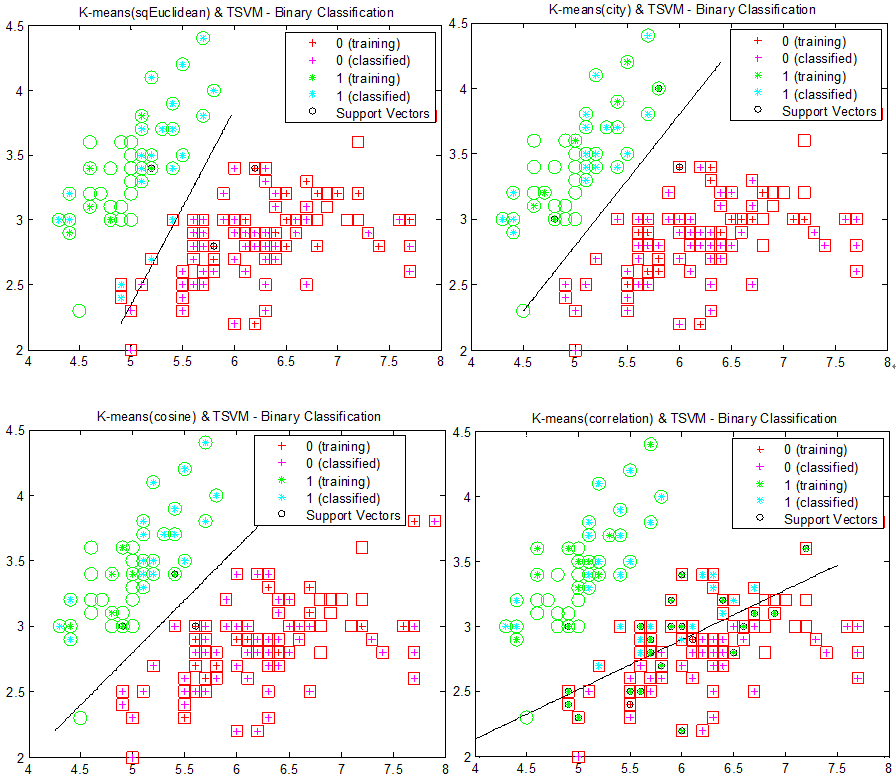
图8:首先对图5的数据进行K-means聚类,以0.2的概率随机抽取聚类中样本作为训练样本,接着对两个类使用SVM进行划分分类面。从左至右,从上至下,使用欧几里得距离、街区距离、余弦距离和相关距离(1-相关系数)进行K-means聚类。圆形和正方形表示正确的分类。
由于训练样本是从聚类样本中随机抽取得到的,原训练样本可能与测试样本相重叠,所以有些圆形和正方形中是中空的。图中所示的结果是分类得到的较好结果。各种距离对应的分类结果较之前相互接近,但付出的代价就是概率。好的分类结果并不会总是出现,甚至会很罕见。可改进的方法还有很多,例如随机抽取时增加原训练样本的比重,缩小测试样本的比重等。这里就不再赘述。
小结
区别于归纳推理(Inductive Inference)从特殊到一般,再从一般到特殊的学习方式,转导推理(Tranductive Inference)是一种从特殊到特殊的统计学习(或分类)方法。在预测样本的类别时,转导推理试图通过局部的标注训练样本进行判断,这与归纳推理先从训练样本中归纳得到一般模型有着很大差异。特别是当训练样本的数量不足以归纳得到全局一般模型时,转导推理能够利用未标注样本补充标注样本的不足。然而转导推理还有很多问题亟待解决,例如KNN每次预测都要遍历所有测试样本,TSVM的精确解如何更好地近似等。
参考文献
- Transduction (machine learning)[EB/OL]. [2012-5-7]. http://en.wikipedia.org/wiki/Transduction_(machine_learning).
- Gammerman A, Vovk V, Vapnik V. Learning by transduction[C]//Proceedings of the Fourteenth conference on Uncertainty in artificial intelligence. Morgan Kaufmann Publishers Inc., 1998: 148-155.
- Chapelle O, Schölkopf B, Zien A. Semi-supervised learning[M]. Cambridge: MIT press, 2006. (美)VladimirN.Vapnik著. 统计学习理论[M]. 许建华,张学工译. 北京: 电子工业出版社, 2004


 浙公网安备 33010602011771号
浙公网安备 33010602011771号