6.6 归并排序

（1）归并排序：

　　归并排序是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组，再合并数组。

　　将数组分解最小之后，然后合并两个有序数组，基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

（2）归并排序分析：

　　　　　

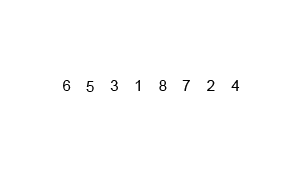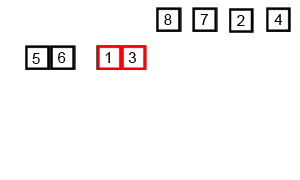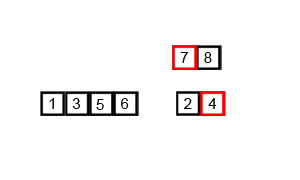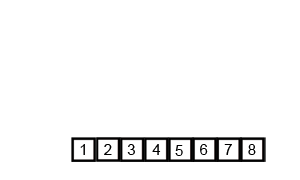
（3）代码实现：

 1 def merge_sort(alist):
 2     """归并排序"""
 3     n = len(alist)
 4     if n <= 1:
 5         return alist
 6     mid = n // 2      # 11.0 / 2 = 5.5        11.0 // 2 =5.0(取整除)
 7 
 8     # left_li 采用归并排序后形成的有序的新的列表
 9     left_li = merge_sort(alist[:mid])     # 传入的是切片分出的新的列表
10 
11     # right_li 采用归并排序后形成的有序的新的列表
12     right_li = merge_sort(alist[mid:])
13 
14     # 将两个有序的子序列合并为一个新的整体
15     # merge(left, right)
16     left_pointer, right_pointer = 0, 0
17     result = []     # 新的列表，用以存放合并结果
18 
19     while left_pointer < len(left_li) and right_pointer < len(right_li):
20         if left_li[left_pointer] < right_li[right_pointer]:
21             result.append(left_li[left_pointer])
22             left_pointer += 1
23         else:
24             result.append(right_li[right_pointer])
25             right_pointer += 1
26     # 循环结束两个切片可能还有剩余，需要将剩下的全部添加到合并结果中
27     result += left_li[left_pointer:]
28     result += right_li[right_pointer:]
29     return result
30 
31 
32 if __name__ == "__main__":
33     li = [54, 26, 93, 17, 77, 31, 44, 55, 20]
34     print(li)
35     sort_list = merge_sort(li)
36     print(li)
37     print(sort_list)

（4）运行结果：

　　　　

（5）时间复杂度：　

　　　　最优时间复杂度：O(nlogn)

　　　　最坏时间复杂度：O(nlogn)

　　　　稳定性：稳定

（6）常见排序算法效率对比：

　　　　

posted @ 2018-07-05 10:36  博观&约取  阅读(214)  评论(0)  编辑  收藏  举报