杭电多校2023第四场

1003

把所有的$a$排个序

然后根据贪心，一定是取连续的段

尺取法取所有可能的段即可(

#include <bits/stdc++.h>
#define pii pair<int,int>
using namespace std;
vector<pii> a;
int mp[1000005];
int T;
int main(){
    std::ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin >> T;
    while (T--){
        int K; 
        cin >> K;
        a.clear();
        for (int i = 1 ; i <= K ; i ++){
            int c;
            cin >> c;
            mp[i] = 0;
            for (int j = 1 ; j <= c ; j ++){
                int x;
                cin >> x;
                a.push_back({x,i});
            }
        }
        sort(a.begin(),a.end());
        int Len = a.size();
        int cnt = 0;
        int ans = 2e9+7;
        for (int l = 0 , r = 0; l < Len ; l ++){
            //cout << a[l].first << " " << a[l].second << endl;
            while (cnt < K && r < Len){
                pii nw = a[r];
                int x = nw.first,y = nw.second;
                mp[y] ++;
                if (mp[y] == 1) cnt ++;
                r ++; 
            }
            //cout << mp[3] << endl;
            if (cnt < K) break;    
            //cout << l << " " << r << endl;
            //cout << a[l].first << " " << cnt << " " << a[r].first << endl;
            ans = min(ans,a[r-1].first - a[l].first);
            pii nw = a[l];
            int x = nw.first,y=nw.second;
            mp[y]--;
            if (mp[y] == 0) cnt--;
        }
        cout << ans << endl;
    }
}

1004

首先根据期望的线性性，每个点是可以单独分开考虑的

也就只需要知道每个点在$k$次操作后不落在自己位置上的答案。

$f_i$表示进行了$i$次操作，某个点在自己的位置上的概率

$f_i = f_{i-1} * \frac{1+(n-1)^2}{n^2} + (1-f_{i-1}) * \frac{2}{n^2}$

前者是考虑了上一次已经在自己的位置上，所以这一次不能交换到这个位置，或者自己和自己交换(+1)

后者是考虑上一次不在自己位置上，通过一次交换换到自己位置上

然后这个东西化简一下就是$f_i = f_{i-1} * \frac{n-2}{n}+\frac{2}{n^2}$

写成矩阵形式

 

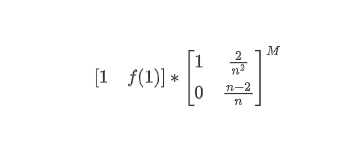
 矩阵快速幂跑一下就好了

#include <bits/stdc++.h>
#define int long long
using namespace std;
int N,M;
int T;
const int MOD = 998244353;
struct Matrix{
    int a[3][3];
    int H,W;
    Matrix operator *(const Matrix b){
        Matrix c;
        memset(c.a,0,sizeof(c.a));
        //cout << H <<" " << W <<" " << b.W << "????"<<endl;
        for (int i = 0 ; i < H; i ++)
            for (int j = 0 ; j < b.W ; j ++)
                for (int k = 0 ; k < W ; k ++){
                    (c.a[i][j] += (1ll * a[i][k] * b.a[k][j])%MOD)%=MOD;
            }
            c.H = H,c.W=b.W;
            return c;
    };
};
int Pow(int x,int y){
    int ans = 1;
    for (;y;){
        if (y & 1) ans = 1ll * ans * x %MOD;
        x = 1ll * x * x % MOD;
        y >>=1;
    }
    return ans;
}
Matrix Pow1(Matrix x,int y){
    Matrix ans;
    ans.a[0][0] = 1;ans.a[0][1] = 0;
    ans.a[1][0] = 0;ans.a[1][1] = 1;
    ans.H = 2,ans.W = 2;
    for (;y;){
        if (y & 1) ans = ans * x;
        x = x * x;
        y >>=1;
    }
    return ans;
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin >> T;
    while (T--){
        cin >> N >> M;
        N%=MOD;
        Matrix ans;
        ans.a[0][0] = 1,ans.a[0][1] = 1;
        int inv = Pow(N,MOD-2),inv1 = Pow(N*N%MOD,MOD-2);
        ans.H = 1,ans.W = 2;
        Matrix k;
        k.a[0][0] = 1,k.a[0][1]=2ll*inv1%MOD;
        k.a[1][0] = 0,k.a[1][1]=1ll*(N-2)*inv%MOD;
        k.H=2,k.W=2;
        Matrix K1 = Pow1(k,M);
        Matrix anss = ans * K1;
        //cout << anss.a[0][1] << endl;
        long long ansss = (N - 1ll * N * anss.a[0][1]%MOD+MOD)%MOD;
        cout << ansss << endl;
    }
    return 0;
}

1006

签到，没啥好说(

注意特判一下$n==2$的case即可

其他的就大力分类一下，为1为2的概率直接算

#include <bits/stdc++.h>
using namespace std;
int main(){
    int T;
    cin >> T;
    while (T--){
        int N;
        cin >> N;
        if (N == 2){
            double a = 1,b=1;
            printf("%.9lf %.9lf\n",a,b);
            continue;
        }
        double NN =N;
        double ans = 2. - 2./NN;
        double dis = 2; 
        printf("%.9lf %.9lf\n",ans,dis);
    }
    return 0;
} 

1007

原形式不太好处理

考虑先莫比乌斯反演一下

变成$ln(n) = \sum_{d|n} f(d)$

两边$exp$一下

变成$n = \prod^{d|n} f(d)$

容易证明的是$f(p^k) = p$

打个表不难发现只有$p^k$处函数有值，其余为$1$

用Pollard-rho分解一下素因子即可。

#include "bits/stdc++.h"
using namespace std;
#define ll long long
const __int128 ONE = 1;
ll qpow(ll a,ll b,ll mod)
{
    ll res = 1;
    while(b)
    {
        if(b & 1) res = ONE * res * a % mod;
        a = ONE * a * a % mod;
        b = b >> 1;
    }
    return res;
}
int Suk[25]={0,2,3,5,7,11,13,17,19,23,29,31,37};
inline bool chk(ll n,ll a,ll b,ll x) 
{
    ll v = qpow(x , a , n);
    if (v == 1) return 1;
    int j = 1;
    while(j <= b)
    {
        if(v == n - 1) break;
        v = ONE * v * v % n;
        j ++;
    }
    if (j > b) return 0;
    return 1;
}
inline bool mr(ll n)
{
    if(n < 3 || n % 2 == 0) return n == 2;
    if(n > 37)
    {
        ll a = n - 1 , b = 0;
        while(a % 2 == 0) a >>= 1 , b ++;
        for(int i = 1 ; i <= 12 ; i ++) if(!chk(n , a ,  b , Suk[i])) return 0;
        return 1;
    }
    else
    {
        for(int i = 1 ; i <= 12 ; i ++) if(n == Suk[i]) return 1;
        return 0;
    }
}
static std::mt19937 MoBaiXHR;
inline ll F(ll x,ll c,ll MOD){return (ONE * x * x % MOD + c) % MOD;}
inline ll ABS(ll x){if(x < 0) return -x;return x;}
ll gcd(ll a,ll b)
{
    if(!b) return a;
    return gcd(b , a % b);
}
inline ll pr(ll n)
{
    if(n == 4) return 2;
    std::uniform_int_distribution<ll> Rand(3 , n - 1);
    ll x = Rand(MoBaiXHR) , y = x , c = Rand(MoBaiXHR);
    x = F(x , c , n) , y = F(F(y , c , n) , c , n);
    for(int lim = 1 ; x != y ; lim = min(lim << 1 , 128))
    {    
        ll cnt = 1;
        for(int i = 0 ; i < lim ; i ++) 
        {
            cnt = ONE * cnt * ABS(x - y) % n;
            if(!cnt) break;
            x = F(x , c , n) , y = F(F(y , c , n) , c , n);
        }
        ll d = gcd(cnt , n);
        if(d != 1) return d;
    }
    return n;
}
ll ans;
inline void MAX(ll z){if(z > ans) ans = z;}
void dfs(ll n)//非质数 
{
    ll d = pr(n);
    while(d == n) d = pr(n);
    ll d2 = n / d;
    if(mr(d)) MAX(d);
    else dfs(d);
    if(mr(d2)) MAX(d2);
    else dfs(d2);
}
ll getans(ll x)
{
    if(mr(x)) return x;
    ans = 0;
    dfs(x);
    return ans;
}
const ll MOD = 998244353;
int main()
{
    srand(time(0));
    int T;scanf("%d",&T);
    while(T --)
    {
        ll x;scanf("%lld",&x);
        if (x == 1) 
        {
            printf("1 ");
            continue; 
        }
        ll res = getans(x);
        while (x%res == 0){
            x/=res;
        }
        if (x == 1) printf("%lld ",res%MOD);
        else printf("1 ");
    }
    return 0;
}

1010

学弟打了个表，把结论猜出来了

猜完之后瞎证明了一下$(n,m)$可以规约到$(n-3,m)$或者$(n,m-3)$

然后就交了一发，然后就过了(

注意特判1*n

#include <bits/stdc++.h>
using namespace std;
int T;
int main(){
    cin >> T;
    while (T--){
        int M,N;
        cin >> M >> N;
        if (M==1 || N ==1){
            cout << (M+N)/2 << '\n';
        }
        else {
            if (M%3 ==0 || N%3 ==0) cout << 2 << '\n';
            else cout << 1 << '\n'; 
        }
    }
    return 0;
}

1011

n<=500

Floyd找最距离，并且统计一下方案数

每次循环$k$的时候，只统计最大标号为$k$的那些环，这样即可保证不重不漏。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 998244353;
int N,M;
int d[505][505],dis[505][505],f[505][505];
signed main(){
    std::ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    int T;
    cin >> T;
    while (T--){
        cin >> N >> M;
        memset(d,63,sizeof(d));
        memset(dis,63,sizeof(dis));
        memset(f,0,sizeof(f));
        for (int i = 1 ; i <= M ; i ++){
            int u,v,w;
            cin >> u >> v >> w;
            d[u][v] = w;
            dis[u][v] = w;
            f[u][v] = 1;
        }
        for (int i = 1 ; i <= N ; i ++)
            dis[i][i] = 0,f[i][i] = 1;
        int INF = 1e18,ans1 = 1e18,ans2 = 0;
        for (int k = 1 ; k <= N ; k ++){
            for (int i = 1 ; i < k ; i ++)
                for (int j = 1 ; j < k ; j ++){
                    if (dis[j][i] == dis[0][0] || d[i][k] ==d[0][0] || d[k][j] == d[0][0]) continue;
                    if (ans1 > dis[j][i] + d[i][k] + d[k][j]){
                        ans1 = dis[j][i] + d[i][k] + d[k][j];
                        ans2 = f[j][i]%MOD;
                    }else if (ans1 == dis[j][i] + d[i][k] + d[k][j]) (ans2 += f[j][i])%=MOD;
                }
            for (int i = 1 ; i <= N ; i ++)
                for (int j = 1 ; j <= N ; j ++){
                    if (i == k || k == j || i == j ) continue;
                    if (dis[i][k] + dis[k][j] < dis[i][j]){
                        dis[i][j] = dis[i][k] + dis[k][j];
                        f[i][j] = 0;
                    }
                    if (dis[i][k] + dis[k][j] == dis[i][j]){
                        (f[i][j] += f[i][k] * f[k][j]%MOD)%=MOD;
                    }
                }
        }
        if (ans1 == INF){
            cout << "-1 -1" <<endl;
        }else cout << ans1 << " " << ans2 << endl;
    }
    return 0;
}

1012

学弟写的，一个不知道是啥的签到题(

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>

#define x first
#define y second

using namespace std;

typedef long long LL;
typedef pair< int, int > PII;

const int N = 100010;
int n;
int qa[N], qb[N];
PII q[N];


int read()
{
    int res = 0, w = 1;
    char ch = getchar();
    while (ch != '-' && !isdigit(ch))
        ch = getchar();
    if (ch == '-')
        w = -1, ch = getchar();
    while (isdigit(ch))
        res = res * 10 + ch - '0', ch = getchar();
    return res * w;
}

void solve() {
    cin >> n;
    memset(q, 0, sizeof q);
    memset(qa, 0, sizeof qa);
    memset(qb, 0, sizeof qb);
    for(int i = 1; i <= n; i ++)
    {
        int a, b;
        cin >> a >> b;
        qa[i] = a;
        qb[i] = b;
        q[i].x = a + b;
        q[i].y = i;
        
    }

    sort(q + 1, q + n + 1);

    LL ans = 0;
    int cnt = 1;
    for(int i = n; i >= 1; i --)
    {
        int id = q[i].y;
        if(cnt % 2) ans = ans + qa[id];
        else ans = ans - qb[id];
        cnt ++;
    }

    cout << ans << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int T = 1;
    cin >> T;

    while (T--)
    {
        solve();
    }

    return 0;
}