2023杭电多校第二场

1001

求个SG然后打表

发现$SG=0$的点满足$t = k_1 * (4*K+2) + (K+1)$

#include <bits/stdc++.h>
using namespace std;
int T,N;
int main(){
    cin >> T;
    while (T--){
        int N,K;
        cin >> K >> N;
        if (N <= K) cout << "Alice\n";
        else if (N%(4*K+2) == K+1) cout << "Bob\n";
        else cout << "Alice\n";
    }
    return 0;
}

附带打表代码.jpg

#include <bits/stdc++.h>
using namespace std;
int K;
bool bk[50005];
long long sg[50005];
vector<int> nw;
int SG(int N){
    if (sg[N]!=-1) return sg[N]; 
    if (N == K+1) return 0;
    if (N == 0) return 0; 
    if (N <= K) return 1;
    nw.clear();
    for (int i = 1 ; i <= N-K-1 ; i ++){
        int sgn = SG(i) ^ SG(N-K-i);
        nw.push_back(sgn); 
    }
    sort(nw.begin(),nw.end());
    for (int i = 0 ; i < 500 ; i ++){
        bk[i] = false;
    }
    for (auto v : nw)
        bk[v] = true;
    for (int i = 0 ; i < 500 ; i ++){
        if (!bk[i]) return sg[N] = i;
    }
}
int main(){
    memset(sg,-1,sizeof(sg));
    int N;
    K = 2;
    for (int i = 1 ; i <= 50 ; i ++)
        if (SG(i) == 0) cout << i << endl;
    return 0;
}

1002

分类讨论，把连续的1和0分别压成一段进行考虑即可。

#include <bits/stdc++.h>
using namespace std;
int T;
char a[100005];
struct Node{
    int Len;
    int Type;
};
vector<Node> nw;
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0); 
    cout.tie(0);
    cin >> T;
    while (T--){
        int N;
        long long K;
        cin >> N >> K;
        bool flag = false;
        int cnt = 0;
        cin >> a[1];
        cnt = 1;
        nw.clear();
        for (int i = 2 ; i <= N ; i++){
            cin >> a[i];
            if (a[i] == '0') flag = true; 
            if (a[i] == a[i-1]) cnt ++;
            else{
                nw.push_back(Node{cnt,a[i-1] - '0'});
                cnt = 1;
            }
        }
        if (N == 1){
            int t = K%2;
            cout <<1-t;
            cout << endl;
            continue;
        }
        if (!flag){
            for (int i = 1 ; i < N ; i ++)
                cout << a[i];
            if(K==1) cout << 0;
            else cout << 1;
            cout << endl;
            continue;
        }
        nw.push_back(Node{cnt,a[N]-'0'});
        int Len = nw.size();
        for (int i = 0 ; i < Len ; i ++){
            if (nw[i].Type == 0 && K > 0){
                K--;
                nw[i].Type = 1;
            }
        }
        for (int i = 0 ;i < Len-1 ; i ++){
            for (int j = 0 ; j < nw[i].Len ; j ++)
                cout << nw[i].Type;
        }
        for (int i = 0 ;i < nw[Len-1].Len - 1;i++){
            cout << nw[Len-1].Type;
        }
        long long t = K%2;
        t = 1ll - t; 
        cout << nw[Len-1].Type;
        cout << endl;
    }
    return 0;
}

1004

队友写的签到，咕咕

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;
typedef long long LL;

const LL mod = 998244353;

LL n;
LL ans;

LL qmi(LL a, LL k)
{
    LL res = 1;
    while(k)
    {
        if(k & 1) res = res * a % mod;
        a = a * a % mod;
        k >>= 1;
    }
    return res;
}

int main()
{
    int T;
    scanf("%d", &T);
    
    while(T --)
    {
        scanf("%lld", &n);
        ans = 1;
//        for(int i = 3; i <= n; i ++)
//            ans = (ans * 2 + 1) % mod;
        if(n >= 3) ans = qmi(2, n - 1) - 1;
        printf("%lld\n", (ans % mod + mod) % mod);
    }    
    
    return 0;
}

1007

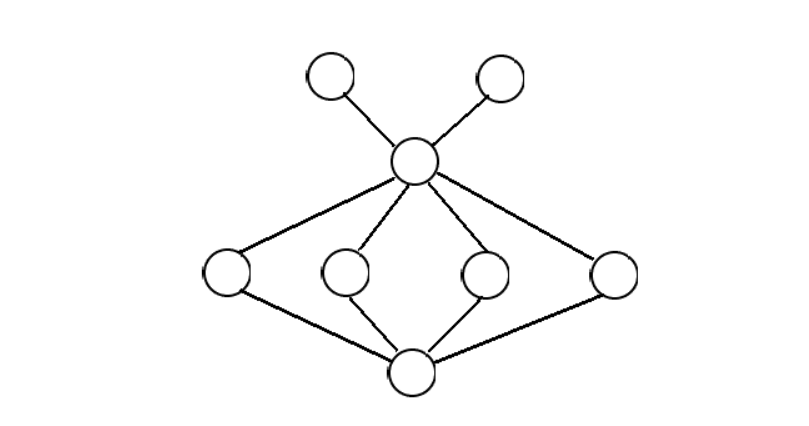
枚举中间和底下两个点

问题转化成两个东西的共同出边点

邻接矩阵存图，bitset取个出边的$and$即可

然后组合数一下，从共同出点选$4$个，其余点选$2$个

如果上点和下点连边，记得把其余点的个数-1

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 1000000007;
bitset<1005> a[1005];
int d[1005];
int fac[1005],inv[1005];
int C(int n,int r){
    return fac[n] * inv[r] % MOD * inv[n-r]%MOD;
}
int Pow(int x,int y){
    int ans = 1;
    for (;y;y>>=1){
        if (y & 1) ans = 1ll *ans * x %MOD;
        x = 1ll * x * x %MOD;
    }
    return ans;
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0); 
    cout.tie(0);
    fac[0] = 1;
    int T;
    cin >> T;
    for (int i = 1 ; i <= 1000 ; i ++)
        fac[i] = 1ll * fac[i-1] * i %MOD;
    inv[1000] = Pow(fac[1000],MOD-2);
    for (int i = 999 ; i >= 1 ; i --)
        inv[i] = 1ll*inv[i+1]*(i+1)%MOD; 
    inv[0] = 1;
    while (T--){
        int N,M;
        cin >> N >> M;
        memset(d,0,sizeof(d));
        for (int i = 1 ; i <= N ; i ++)
            a[i].reset();
        for (int i =1 ; i <= M ; i ++){
            int u,v;
            cin >> u >> v;
            a[u].set(v,1);
            a[v].set(u,1);
            d[u] ++;
            d[v] ++; 
        }
        int ans = 0;
        for (int i = 1 ; i <= N ; i ++){
            for (int j = 1 ; j <= N ; j ++){
                if ( i == j) continue;
                bitset<1005> s;
                s = a[i] & a[j];
                int t = s.count();
                if (t < 4) continue;
                if (d[i] < 6) continue;
                int tt = d[i] - 4;
                if (a[i][j] == 1) tt --;
                ans = (ans + 1ll * C(t,4) * C(tt,2) %MOD)%MOD;
            }
        }
        cout << ans << endl;
    }
    return 0;
}

1009

 

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N = 1000010;

char s[N];

int main()
{
    int T;
    scanf("%d", &T);
    
    while(T --)
    {
        scanf("%s", s);
        int n = strlen(s);
        
        int ans = 0;
        for(int i = 1; i < n;i ++)
        {
            if(s[i] == s[i - 1]) ans ++;
        }
        
        printf("%d\n", ans);
    }    
    
    return 0;
} 

队友写的签到

1010

根据数据范围不难猜测应该可以$O(NM)$的dp，但是空间存不下

我的想法大概是$f[i][j]$表示最后一个1在$i$号点，上一个$1$和它的距离为$j$

转移随便写写，会发现可以用后缀$min$优化一下

然后会发现其实只有距离为$m$以下的那些信息是有意义的，滚动一下dp数组就好了，变成$m*m$，足以通过

然后喂给队友之后他似乎改了改我的状态表示，不过过了(

代码是队友写的，做法类似，但是他拉了个单调栈维护后缀min

#include <iostream>
#include <list>
#include <cstring>
using namespace std;

const int N = 2e4 + 5;
const int M = 2e3 + 5;
const int INF = 0x3f3f3f3f;

struct D {
    int p, v;
};

int n, m;
int a[N];
list<D> stk[N];

void solve() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        stk[i].clear();
    }
    if (n == m) {
        int Min1 = INF;
        int Min2 = INF;
        for (int i = 1; i <= n; i++) {
            if (a[i] <= Min1) {
                Min2 = Min1;
                Min1 = a[i];
            } else if (a[i] < Min2) {
                Min2 = a[i];
            }
        }
        printf("%d\n", Min1 + Min2);
        return;
    }
    int ans = INF;
    for (int i = 2; i <= n; i++) {
        for (int j = i - 1, e = max(i - m + 1, 1); j >= e; j--) {
            if (i <= m) {
                int k = a[i] + a[j];
                if (stk[i].empty() || k < stk[i].back().v) {
                    stk[i].push_back((D){j, k});
                }
                if (i >= n - m + 2 && j >= n - m + 1) {
                    ans = min(ans, k);
                }
                continue;
            }
            if (stk[j].empty()) {
                continue;
            }
            int res = a[i] + stk[j].back().v;
            if (stk[j].back().p == i - m) {
                stk[j].pop_back();
            }
            if (stk[i].empty() || res < stk[i].back().v) {
                stk[i].push_back((D){j, res});
            }
            if (i >= n - m + 2 && j >= n - m + 1) {
                ans = min(ans, res);
            }
        }
    }
    printf("%d\n", ans);
}

int main() {
    int T; scanf("%d", &T);
    while (T--) {
        solve();
    }
    return 0;
}

 1011

考虑这东西怎么求

f(n,k)表示n个数，k处划分

$f(n,k) = \sum \frac{1}{n} *\frac{k}{i-1}$

$=\sum \frac{k}{n}*\sum \frac{1}{i}$

不难发现单峰

可以三分，也可以把后面那个调和级数近似一下求个导(

#include <bits/stdc++.h>
using namespace std;
int N,K,T;
double as,Sum[10005];
double Calc(int n,int k){
    if ( k == 0 ) return 1./n;
    return (1. * k)/(1.*n) * (Sum[n-1] - Sum[k-1]);
}
int main(){
    cin >> T;
    for (int i = 1 ; i <= 10000; i ++)
        Sum[i] = Sum[i-1] + 1./i;
    while (T--){
        cin >> N;
        int pos = 0;
        double T = 1.*N/(exp(1)) , p = 1.0/N;
        for (int i = max(int(T-20),1) ; i <= min(int(T+20),N-1) ; i ++){
            if (Calc(N,i) > p){
                p = Calc(N,i);
                pos = i;
            }
        }
        cout << pos << '\n';
    }
    return 0;
} 

 1006

 

问题转化成$n$个点中能否拿出一个最小子集，连线包住$m$个点

不难猜测最终答案一定是从$n$个点里取一个凸包出来，包住这$m$个点

包住这$m$个点，换句话说，$m$个点都在线段的同侧

$n$很小，大力把所有边跑出来，看$m$个点是否在同侧，如果是则是可能作为答案的边，不是则不可能

然后找到一个最小环即可。

#include <bits/stdc++.h>
using namespace std;
int T,N,M;
const int mx = 5005;
struct Point{
    int x,y;
}a[mx],b[mx];
int Check(Point a, Point b, Point c){
    return (a.x - c.x) *(b.y - c.y) - (a.y - c.y) * (b.x - c.x);
}
const int inf = 1e9+7;
int dis[505][505];
int main(){
    cin >> T;
    while ( T-- ){
        cin >> N >> M;
        for (int i = 1 ; i <= N ;  i++){
            cin >> a[i].x >> a[i].y;
        }
        for (int i = 1 ; i <= M ; i ++){
            cin >> b[i].x >> b[i].y;
        }
        memset(dis,63,sizeof(dis));
        for (int i = 1 ; i <= N ; i ++)
            for (int j = 1 ; j <= N ; j ++){
                if (i != j){
                    dis[i][j] = 1;
                    for (int k = 1 ; k <= M ; k ++){
                        if (Check(a[i],a[j],b[k]) <= 0) dis[i][j] = inf; 
                    }
                }
            }
        for (int k = 1 ; k <= N ; k ++)
            for (int i = 1 ; i <= N ; i ++)
                for (int j = 1 ; j <= N ; j ++){
                    dis[i][j] = min(dis[i][j] , dis[i][k] + dis[k][j]);
                }
        int ans = inf;
        for (int i = 1 ; i <= N ; i ++)
            if (dis[i][i] < ans) ans = dis[i][i];
        if (ans == inf) cout << "-1\n";
        else cout << ans << '\n';
    }
    return 0;
}