卡特兰数
$Catalan$
今天跟着$asuldb$复习了一下组合数学,发现$Catalan$数一直不是很明白,那就再学习一下吧.
关于卡特兰数的题目有一种特别好用的方法,首先打表/手玩几组解,如果看起来像卡特兰...那就用吧!$1, 2, 5, 14, 42, 132$
卡特兰数是比利时数学家卡特兰发明的,有几个非常经典的应用:
1 出栈序列:将$1-n$依次加入到一个无穷大的栈里面,可以随时出栈,求有多少种出栈序列.
可以将这道题抽象一下,进栈为$1$,出栈为$-1$,那么出栈序列就是一个由$1,-1$组成的序列,这里面有$n$个$1$,所以答案就是$C_{2n}^n$...这样做是错的...
因为每次出栈的时候栈不能是空的,所以对序列做一个前缀和,必须每个前缀和都非负才满足条件。对于一个不合法的序列,首先找到它第一个不合法的位置,前缀和一定等于-1,然后将以他结尾的前缀取反,这样就会有$n+1$个$1$了,此时可以发现由$n+1$个$1$,$n-1$个$0$构成的序列与不合法序列是一一对应的(找到前缀和第一次为$1$的位置取反就可以回到原先的不合法序列),这样的方案数是$C_{2n}^{n-1}$,所以总的答案就是$C_{2n}^n-C_{2n}^{n-1}$
1.5 长度为$2n$的合法括号序列计数:左括号视为进栈,右括号视为出栈,同上.
2.二叉树形态计数:一个简单的树形$dp$,$f_x=\sum_{i=0}^{x-1}f_i\times f_{x-i-1}$.令人惊讶的是这竟然就等于卡特兰数;
3.$n+2$个顶点的凸多边形的三角剖分计数:这个和二叉树比较像,也是考虑剖分一次后就将多边形分成了两个部分,乘法原理+加法原理;
4.棋盘上走路,不越过$(1,1)-(n,n)$这条线的走法:考虑将向右走视为加一,向上走视为减一,那么任意时间不为负...和第一个是一样的.
5.圆上$n$个点,两两配对并连线,要求连线不能交叉的方案数:首先固定一个点,有$n-1$种连线方法,其中每一种都将圆分成了两个部分,还是和二叉树那个差不多.
那么卡特兰数有好几个计算公式,下面来写一下:
$$C_n=\sum_{i=0}^{n-1}C_i\times C_{x-i-1}$$
$$C_n=\binom {n}{2n}-\binom{n-1}{2n}$$
$$C_n=\frac{\binom {n}{2n}}{n+1}$$
$$C_n=C_{n-1}\times \frac{4\times n-2}{n+1}$$
不过这第四个公式真的有用吗...
然而仅仅考卡特兰数太没意思了,出题人往往想出一些奇奇怪怪的方法提高难度:
$Part$ $1$:你知道这就是求卡特兰数但是就是求不出来系列:
取模:
取模与高精相比看起来是很良心的一种题目,比如说这个:
有趣的数列:https://www.lydsy.com/JudgeOnline/problem.php?id=1485
题意概述:求满足以下条件且长度为$2n$的序列个数$\%P$:$n<=10^6且P<=10^9$
(1)它是从$1$到$2n$共$2n$个整数的一个排列${a_i}$;
(2)所有的奇数项满足$a_1<a_3<...<a_{2n-1}$,所有的偶数项满足$a_2<a_4<...<a_{2n}$;
(3)任意相邻的两项$a_{2i-1}与a_{2i}(1<=i<=n)$满足奇数项小于偶数项,即:$a_{2i-1}<a_{2i}$。
通过理智的分析(打表找规律),发现答案就是卡特兰数,这里的$n$这么大,那么肯定是不能用第一个公式了,于是你愉快地运用了第二个公式并使用快速幂求阶乘逆元,然后$WA$了.
这时才发现$P$不一定是质数,所以有时候做着做着答案就乱套了(样例都过不了).于是这里要运用一个类似于高精度的技巧,首先最终的答案肯定是一个整数,那么如果运用第三个公式就不用担心除法出现小数的问题了.这就是问题的关键所在:分子上的数的唯一分解式中每一项的系数都不小于分母,所以可以对分子分母分别分解质因数,直接求出最终答案的唯一分解式.因为乘法取模对模数没有限制,就可以做了.
关于分解质因数还有一点小建议:如果对效率没有很高的追求,可以用根号算法分解,如果对效率有着极致的追求,那么可以利用线性筛法的性质,在筛的同时记录每个数的最小质因子,每次除以最小质因子,复杂度约为$logN$.

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # include <algorithm> 6 # include <cmath> 7 # define R register int 8 # define ll long long 9 10 using namespace std; 11 12 const int maxn=2000006; 13 int n,p,vis[maxn],pri[maxn],h,z[maxn],c[maxn]; 14 ll ans=1,f[maxn]; 15 16 ll qui (ll a,ll b,ll p) 17 { 18 ll s=1; 19 while(b) 20 { 21 if(b&1) s=s*a%p; 22 a=a*a%p; 23 b>>=1; 24 } 25 return s%p; 26 } 27 28 void ad (int x,int v) 29 { 30 while(vis[x]) 31 { 32 c[ z[x] ]+=v; 33 x/=z[x]; 34 } 35 c[x]+=v; 36 } 37 38 void init (int x) 39 { 40 for (R i=2;i<=x;++i) 41 { 42 if(!vis[i]) pri[++h]=i; 43 for (R j=1;j<=h&&i*pri[j]<=x;++j) 44 { 45 vis[ i*pri[j] ]=1; 46 z[ i*pri[j] ]=pri[j]; 47 if(i%pri[j]==0) break; 48 } 49 } 50 } 51 52 int main() 53 { 54 scanf("%d%d",&n,&p); 55 init(2*n); 56 for (R i=2;i<=2*n;++i) ad(i,1); 57 for (R i=2;i<=n;++i) ad(i,-1); 58 for (R i=2;i<=n+1;++i) ad(i,-1); 59 for (R i=2;i<=2*n;++i) 60 if(c[i]) ans=(ans*qui(i,c[i],p))%p; 61 printf("%lld",ans); 62 return 0; 63 }
还有的题目就比较凉心了,(为了让你免去取模的麻烦),干脆不取模了.
树屋阶梯:https://www.lydsy.com/JudgeOnline/problem.php?id=2822
一道题意不好概括的题目.
考虑使用二叉树的分析方式,首先将阶梯从某一层分开,那么上面就是$C_i$,下面就是$C_{n-i}$,看起来非常有道理,然而是错误的,举个例子:
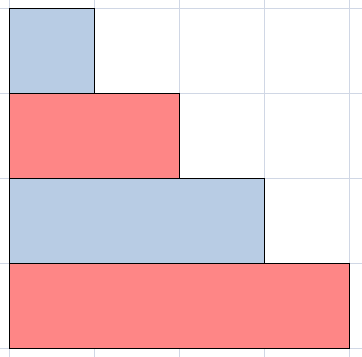
这样的阶梯可能在好几种分层中被认为是多种方案...
那么换一种分层方式:
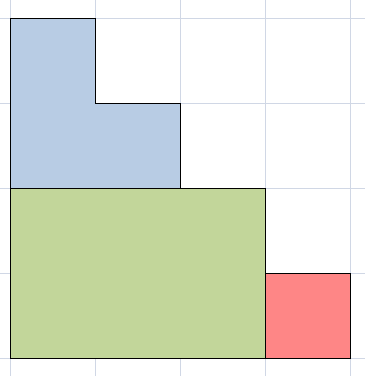
也就是说上下两个子阶梯的大小加起来正好比总大小小$1$,这个绿色的大块直接用一块填上,蓝,红两部分还是$C_i \times C_{n-i-1}$,这样的好处是一定不重复.
高精度的问题其实没有想象中那么难做,依旧沿用上一题的思想,分解完质因数后只需要一个高精度快速幂或朴素乘法即可,乘法相对还是比较简单的.

1 # include <cstdio> 2 # include <iostream> 3 # define maxn 100005 4 # define R register int 5 # define ll long long 6 7 using namespace std; 8 9 ll t,cat[maxn*100]; 10 int n,a,u[maxn],d[maxn]; 11 12 void print () 13 { 14 int len=cat[0]; 15 for (R i=len;i>=1;--i) 16 printf("%lld",cat[i]); 17 } 18 19 void mul (ll x) 20 { 21 int w=0; 22 for (R i=1;i<=cat[0];++i) 23 { 24 cat[i]*=x; 25 cat[i]+=w; 26 w=cat[i]/10; 27 cat[i]%=10; 28 } 29 while (w) 30 { 31 cat[ ++cat[0] ]+=w; 32 w=cat[ cat[0] ]/10; 33 cat[ cat[0] ]%=10; 34 } 35 } 36 37 ll qui (int a,int b) 38 { 39 ll s=1; 40 while (b) 41 { 42 if(b&1LL) s*=a; 43 a*=a; 44 b>>=1LL; 45 } 46 return s; 47 } 48 49 int main() 50 { 51 scanf("%d",&n); 52 for (R i=2;i<=n;++i) 53 { 54 a=n+i; 55 for (R j=2;j*j<=a;++j) 56 while (a%j==0) a/=j,u[j]++; 57 if(a>1) u[a]++; 58 a=i; 59 for (R j=2;j*j<=a;++j) 60 while (a%j==0) a/=j,d[j]++; 61 if(a>1) d[a]++; 62 } 63 cat[0]=cat[1]=1; 64 for (R i=2;i<=2*n;++i) 65 { 66 if(!u[i]) continue; 67 u[i]-=d[i]; 68 if(!u[i]) continue; 69 t=qui(i,u[i]); 70 if(t!=1) mul(t); 71 } 72 print(); 73 return 0; 74 }
$Part$ $2$:根本看不出来是卡特兰数系列:
其实严格来讲这几道题确实不是卡特兰数,但是推式子的思想有一些相似之处:
生成字符串:https://www.lydsy.com/JudgeOnline/problem.php?id=1856
题意概述:将$n$个$1$,$m$个$0$组成一个字符串,要求任意前缀中$1$的个数不能少于$0$的个数,求方案数.
其实这题不算非常难想,但如果对于卡特兰数的式子不明白本质的话就很难做了.
依旧是找到第一个不满足条件的位置翻转,嗯,没了.$C_{n+m}^m-C_{n+m}^{m-1}$,这题挺良心的,对质数取模.

1 # include <cstdio> 2 # include <iostream> 3 # define R register int 4 # define mod 20100403 5 6 const int maxn=2000006; 7 int f[maxn]; 8 int n,m,ans; 9 10 int inv (int a) 11 { 12 int s=1,b=mod-2; 13 while(b) 14 { 15 if(b&1) s=1LL*s*a%mod; 16 a=1LL*a*a%mod; 17 b>>=1; 18 } 19 return s%mod; 20 } 21 22 int C (int n,int m) 23 { 24 return 1LL*f[n]*inv(f[m])%mod*inv(f[n-m])%mod; 25 } 26 27 int main() 28 { 29 scanf("%d%d",&n,&m); 30 n+=m; 31 f[0]=1; 32 for (R i=1;i<=n;++i) 33 f[i]=1LL*f[i-1]*i%mod; 34 ans=((C(n,m)-C(n,m-1))%mod+mod)%mod; 35 printf("%d",ans); 36 return 0; 37 }
网格:https://www.lydsy.com/JudgeOnline/problem.php?id=3907
题意概述:在一个$n \times m$的网格里往上或往右走,不能超过$(1,1)-(n,n)$这条线,求方案数;$n,m<=5000$
其实还是很水的,依旧考虑一样的翻转做法,将右走视为$1$,上走视为$-1$.不过这道题让人有点难受,又没有取模,高精度.$C_{n+m}^{n}-C_{n+m}^{n+1}$

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # define R register int 5 6 using namespace std; 7 8 const int maxn=10009; 9 int n,m; 10 int pri[10009]; 11 int a[10000],b[10000]; 12 13 void print() 14 { 15 for (R i=a[0];i>=1;--i) 16 printf("%d",a[i]); 17 } 18 19 void ad (int x,int v) 20 { 21 for (R i=2;i*i<=x;++i) 22 while (x%i==0) pri[i]+=v,x/=i; 23 if(x!=1) pri[x]+=v; 24 } 25 26 void mul1 (int n) 27 { 28 for (R i=1;i<=a[0];++i) 29 a[i]*=n; 30 for (R i=1;i<=a[0]+5;++i) 31 a[i+1]+=a[i]/10,a[i]%=10; 32 a[0]+=5; 33 while (a[ a[0] ]==0&&a[0]) a[0]--; 34 } 35 36 void mul2 (int n) 37 { 38 for (R i=1;i<=b[0];++i) 39 b[i]*=n; 40 for (R i=1;i<=b[0]+5;++i) 41 b[i+1]+=b[i]/10,b[i]%=10; 42 b[0]+=5; 43 while (b[ b[0] ]==0&&b[0]) b[0]--; 44 } 45 46 void sub() 47 { 48 for (R i=1;i<=a[0];++i) 49 if(a[i]>=b[i]) a[i]-=b[i]; 50 else 51 { 52 a[i+1]--; 53 a[i]=a[i]+10-b[i]; 54 } 55 while (a[ a[0] ]==0&&a[0]) a[0]--; 56 } 57 58 int main() 59 { 60 scanf("%d%d",&n,&m); 61 a[0]=a[1]=b[0]=b[1]=1; 62 for (R i=2;i<=n+m;++i) 63 ad(i,1); 64 for (R i=2;i<=m;++i) 65 ad(i,-1); 66 for (R i=2;i<=n;++i) 67 ad(i,-1); 68 for (R i=2;i<=10000;++i) 69 { 70 if(!pri[i]) continue; 71 for (R j=1;j<=pri[i];++j) 72 mul1(i); 73 } 74 memset(pri,0,sizeof(pri)); 75 for (R i=2;i<=n+m;++i) 76 ad(i,1); 77 for (R i=2;i<=m-1;++i) 78 ad(i,-1); 79 for (R i=2;i<=n+1;++i) 80 ad(i,-1); 81 for (R i=2;i<=10000;++i) 82 { 83 if(!pri[i]) continue; 84 for (R j=1;j<=pri[i];++j) 85 mul2(i); 86 } 87 sub(); 88 print(); 89 return 0; 90 }
---shzr



 浙公网安备 33010602011771号
浙公网安备 33010602011771号