Lucas定理
之前的数论全都塞在一篇里,都快没法看了...现在我决定把它拆开。如果有一些比较零散的就先放在那里。
lx老师画风突变,给我们布置了大量毒瘤数论。于是我...开始做。
首先说一下$Lucas$定理:
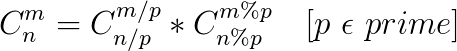
就是这么一个很奇妙的公式,至于为什么...抱歉不会证。
所以它有什么用呢?主要是用于$n,m$非常大,但是$p$还不算很大的时候快速处理组合数取模。拿到这个式子,我们对于前一部分递归求解,后一部分就可以直接算。直接算也是需要技巧的!
·$p$真的非常小:开一个二维数组,用递推预处理组合数;
·$p$大约在$10^5$:用组合数的通项公式:

预处理阶乘以及阶乘的逆元,对于一般的题目这样就足够了,附一份代码:
1 void init() 2 { 3 f[0]=inv[0]=1; 4 for (R i=1;i<p;++i) 5 { 6 f[i]=f[i-1]*i%p; 7 inv[i]=quick_pow(f[i],p-2); 8 } 9 }
·很多题解说Lucas只能处理$p<=10^5$的数据,然而并不是!观察发现,导致耗费时间最多的其实就是预处理逆元,达到了惊人的$O(PlogP)$。我们知道对于$1-n$的逆元是可以线性递推的,那么阶乘会不会也可以呢?答案是肯定的,感谢lx老师的毒瘤题让我学会了新知识。
1 inv[p-1]=qui(p-1,p-2); 2 for (R i=p-1;i>=1;--i) 3 inv[i-1]=1LL*inv[i]*i%p;
至于为什么能这么做...并不是非常清楚。
在cry大佬的教导下我发现这个东西真是非常显然了,思考一下逆元的本质,就会发现:
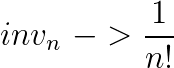

其实就是这样的简单,然而我也确实想不到。
下面粘一个第二种预处理的全代码:
卢卡斯定理:https://www.luogu.org/problemnew/show/P3807

1 // luogu-judger-enable-o2 2 # include <cstdio> 3 # include <iostream> 4 # define ll long long 5 6 using namespace std; 7 8 int T; 9 ll f[100005],inv[100005]; 10 ll n,m,p; 11 12 ll c(ll n,ll m) 13 { 14 if(n<m) return 0; 15 return (f[n]*inv[m]%p)*inv[n-m]%p; 16 } 17 18 ll lucas(ll n,ll m) 19 { 20 if(m==0) 21 return 1; 22 else 23 return (ll)lucas(n/p,m/p)*c(n%p,m%p)%p; 24 } 25 26 ll quick_pow(ll x,ll c) 27 { 28 ll s=1; 29 while (c) 30 { 31 if(c&1) s=s*x%p; 32 x=x*x%p; 33 c=c>>1; 34 } 35 return s%p; 36 } 37 38 void firs() 39 { 40 f[0]=inv[0]=1; 41 for (int i=1;i<p;++i) 42 { 43 f[i]=f[i-1]*i%p; 44 inv[i]=quick_pow(f[i],p-2); 45 } 46 } 47 48 int main() 49 { 50 scanf("%d",&T); 51 while (T--) 52 { 53 scanf("%lld%lld%lld",&n,&m,&p); 54 firs(); 55 printf("%lld\n",lucas(n+m,m)); 56 } 57 return 0; 58 }
这时候我们发现一个小问题:如果$P$不是质数呢?可以用一个非常毒瘤的$exlucas$,据说省选都不考的东西,然而lx老师也当做课后题布置了下来。
扩展lucas是有一种弱化版的,就是说P虽然不是质数,但是每个质因子也只出现一次,比如说古代猪文那道题:
[SDOI2010]古代猪文:https://www.luogu.org/problemnew/show/P2480
现在做这种题我NOIP是不是要凉...学姐说我应该看看费马小定理的题目,然后一查就查到了这个题;
题意概述:其实这题没法概述,不如贴个图:
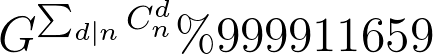
所以这道题就是求这个式子的值啦。$n,g<=1,000,000,000$
这题的幂实在是比较大,所以快速幂也无能为力了,但我们还有别的方法。一般题目的模数就是用来限制答案大小的,然而这里的模数非常有用。根据欧拉定理,如果$n$为质数,$a^{(n-1)}\space mod \space n=0$,因为这道题的模数是个质数,所以一定互质,可以用这个定理来化简式子:(如果$G$正好等于模数就不互质了,直接特判一下输出0)。
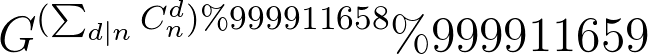
这样只要把上面那个东西求出来就可以使用快速幂算$G$的幂次方了。$n$虽然是挺大,但是开完根号就不算非常大了,于是我们可以试一试在根号时间内分解因子。如果一个数是$n$的因子且它大于根号$n$,那么用$n$除以它必然可以得到一个小于$n$的因子,所以枚举小于根号$n$的数再用$n$去除,就可以得到$n$的所有因子,还是要特判一下完全平方数的情况防止加重了。
现在就只有一个问题了:
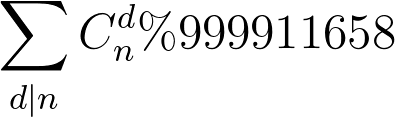
组合数取模!好的,lucas...
然而事情并没有那么简单,理智分析 发现这回的模数不是质数了啊...所以写一个循环看看它有哪些质数因子:
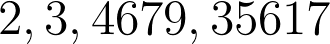
其实还是比较好的,毕竟没有重复的因子,如果有重复因子那就更是麻烦到了一个新境界。所以怎么求呢?
首先对于这每一个质数因子进行$lucas$,求出来四个解:

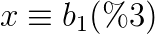


因为要同时满足这四个方程,所以就用中国剩余定理合并一下答案即可.

1 // luogu-judger-enable-o2 2 # include <cstdio> 3 # include <iostream> 4 # include <cmath> 5 # define LL long long 6 7 const int mod=999911659; 8 const int a[5]={2,3,4679,35617}; 9 int n,g,ans; 10 int f[5][35699],ni[5][35699]; 11 int b[5]; 12 int x; 13 14 void exgcd(int a,int b,int &x,int &y) 15 { 16 if(b==0) 17 { 18 x=1; 19 y=0; 20 return ; 21 } 22 exgcd(b,a%b,y,x); 23 y-=(LL)a/b*x; 24 } 25 26 int qui_pow(int x,int n,int p) //求x^n%p 27 { 28 int s=1; 29 x=x%p; 30 while (n) 31 { 32 if(n&1) s=(LL)x*s%p; 33 x=(LL)x*x%p; 34 n=n>>1; 35 } 36 return s%p; 37 } 38 39 void firs(int x) 40 { 41 f[x][0]=1; 42 ni[x][0]=1; 43 for (int i=1;i<a[x];++i) 44 { 45 f[x][i]=f[x][i-1]*i%a[x]; 46 ni[x][i]=qui_pow(f[x][i],a[x]-2,a[x]); 47 } 48 } 49 50 int c(int n,int m,int x) 51 { 52 if(n<m) return 0; 53 return ((LL)f[x][n]*ni[x][m]%a[x])*(LL)ni[x][n-m]%a[x]; 54 } 55 56 int lucas(int n,int m,int x) 57 { 58 if(m==0) 59 return 1; 60 else 61 return (LL)lucas(n/a[x],m/a[x],x)%a[x]*(LL)c(n%a[x],m%a[x],x)%a[x]; 62 } 63 64 int crt() 65 { 66 int m,M=999911658,ans=0; 67 for (int i=0;i<4;++i) 68 { 69 m=M/a[i]; 70 m%=a[i]; 71 int x,y; 72 exgcd(m,a[i],x,y); 73 x=(x%a[i]+a[i])%a[i]; 74 m=M/a[i]; 75 x=(LL)x*m%M; 76 ans=(ans+(LL)x*b[i]%M)%M; 77 } 78 return ans; 79 } 80 81 signed main() 82 { 83 scanf("%d%d",&n,&g); 84 if(mod==g) 85 { 86 printf("0"); 87 return 0; 88 } 89 for (int i=0;i<4;++i) 90 firs(i); 91 g=g%999911658; 92 for (int i=1;i*i<=n;++i) 93 { 94 if (n%i) continue; 95 for (int j=0;j<4;++j) 96 b[j]=lucas(n,i,j); 97 ans=(crt()+ans)%999911658; 98 if(i*i!=n) 99 { 100 for (int j=0;j<4;++j) 101 b[j]=lucas(n,n/i,j); 102 ans=(crt()+ans)%999911658; 103 } 104 } 105 printf("%d",qui_pow(g,ans,999911659)); 106 return 0; 107 }
礼物:https://www.luogu.org/problemnew/show/P2183
题意概述:

Exlucas板子题,几乎就是一路照着题解改过来的,等联赛完了再复习吧.

1 # include <cstdio> 2 # include <iostream> 3 # define R register int 4 # define ll long long 5 6 using namespace std; 7 8 ll n,m,p,sum; 9 int h; 10 ll w[7],a[12]; 11 ll pr[12],po[12]; 12 ll ans=1; 13 14 ll qui (ll a,ll b,ll p) 15 { 16 ll s=1; 17 while (b) 18 { 19 if(b&1LL) s=s*a%p; 20 a=a*a%p; 21 b=b>>1LL; 22 } 23 return s; 24 } 25 26 void ex_gcd (ll a,ll b,ll &x,ll &y) 27 { 28 if(!b) { x=1LL,y=0LL; return ; } 29 ex_gcd(b,a%b,y,x); 30 y-=a/b*x; 31 } 32 33 ll inv (ll a,ll p) 34 { 35 ll x,y; 36 ex_gcd(a,p,x,y); 37 return (x%p+p)%p; 38 } 39 40 ll crt () 41 { 42 ll ans=0; 43 ll x,y,m,pri; 44 for (R i=1;i<=h;++i) 45 { 46 pri=po[i]; 47 m=p/pri; 48 m%=pri; 49 ex_gcd(m,pri,x,y); 50 x=(x%pri+pri)%pri; 51 m=p/pri; 52 x=x*m%p; 53 ans=(ans+x*a[i])%p; 54 } 55 return ans; 56 } 57 58 ll fac (ll n,ll Pr,ll Po) 59 { 60 if(n==0) return 1; 61 ll ans=1; 62 for (R i=2;i<=Po;++i) 63 if(i%Pr) ans=ans*i%Po; 64 ans=qui(ans,n/Po,Po); 65 for (R i=2;i<=n%Po;++i) 66 if(i%Pr) ans=ans*i%Po; 67 return ans*fac(n/Pr,Pr,Po)%Po; 68 } 69 70 ll C (ll n,ll m,ll Pr,ll Po) 71 { 72 if(m>n) return 0; 73 ll t=0; 74 ll a=fac(n,Pr,Po),b=fac(m,Pr,Po),c=fac(n-m,Pr,Po); 75 for (ll i=n;i;i/=Pr) t+=i/Pr; 76 for (ll i=m;i;i/=Pr) t-=i/Pr; 77 for (ll i=n-m;i;i/=Pr) t-=i/Pr; 78 return qui(Pr,t,Po)*a*inv(b,Po)%Po*inv(c,Po)%Po; 79 } 80 81 ll Lucas (ll n,ll m) 82 { 83 for (R i=1;i<=h;++i) 84 a[i]=C(n,m,pr[i],po[i])%p; 85 return crt(); 86 } 87 88 void div (ll p) 89 { 90 for (R i=2;i*i<=p;++i) 91 { 92 if(p%i==0) 93 { 94 ++h; 95 pr[h]=i; 96 po[h]=1; 97 while (p%i==0) po[h]*=i,p/=i; 98 } 99 } 100 if(p>1) pr[++h]=p,po[h]=p; 101 } 102 103 int main() 104 { 105 scanf("%lld",&p),div(p); 106 scanf("%lld%lld",&n,&m); 107 for (R i=1;i<=m;++i) 108 scanf("%lld",&w[i]),sum+=w[i]; 109 if(sum>n) { puts("Impossible"); return 0; } 110 for (R i=1;i<=m;++i) 111 ans=(ans*Lucas(n,w[i]))%p,n-=w[i]; 112 printf("%lld",ans); 113 return 0; 114 }
combination:https://www.lydsy.com/JudgeOnline/problem.php?id=2982
题意概述:

小清新题目,纯属模板;即使这样我也WA了两次,现在真是手残到一定境界了。

1 # include <cstdio> 2 # include <iostream> 3 # define R register int 4 5 using namespace std; 6 7 const int p=10007; 8 const int maxn=10010; 9 int T; 10 int n,m; 11 int f[maxn],inv[maxn]; 12 13 int qui (int a,int b) 14 { 15 int s=1; 16 while (b) 17 { 18 if(b&1) s=s*a%p; 19 a=a*a%p; 20 b>>=1; 21 } 22 return s; 23 } 24 25 void init() 26 { 27 f[0]=inv[0]=1; 28 for (R i=1;i<=p;++i) 29 { 30 f[i]=f[i-1]*i%p; 31 inv[i]=qui(f[i],p-2); 32 } 33 } 34 35 int c (int n,int m) 36 { 37 if(n<m) return 0; 38 return (f[n]*inv[m]%p)*inv[n-m]%p; 39 } 40 41 int Lucas (int n,int m) 42 { 43 if(m==0) return 1; 44 return Lucas(n/p,m/p)*c(n%p,m%p)%p; 45 } 46 47 int main() 48 { 49 scanf("%d",&T); 50 init(); 51 while (T--) 52 { 53 scanf("%d%d",&n,&m); 54 printf("%d\n",Lucas(n,m)); 55 } 56 return 0; 57 }
超能粒子炮·改:https://www.lydsy.com/JudgeOnline/problem.php?id=4591
题意概述:
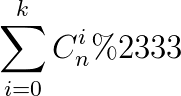
$n,k<=10^{18}$
首先根据$Lucas$打一个表.显然$n\p,n\%p$是不会变的,所以我们只看$i$的部分;

利用和式求和的方法,把相同的归类到一起,就可以迭代求解了:

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # define ll long long 5 # define R register int 6 7 using namespace std; 8 9 const int p=2333; 10 int T; 11 ll n,k,t,ans,x; 12 int f[3000],inv[3000]; 13 int C[p+1][p+1]; 14 15 ll qui (ll a,ll b) 16 { 17 ll s=1; 18 while (b) 19 { 20 if(b&1) s=s*a%p; 21 a=a*a%p; 22 b=b>>1; 23 } 24 return s%p; 25 } 26 27 void init() 28 { 29 f[0]=inv[0]=1; 30 for (int i=1;i<=p;++i) 31 { 32 f[i]=f[i-1]*i%p; 33 inv[i]=qui(f[i],p-2); 34 } 35 C[0][0]=1; 36 for (R i=1;i<=p;++i) 37 { 38 C[i][0]=1; 39 for (R j=1;j<=i;++j) 40 C[i][j]=(C[i-1][j]+C[i-1][j-1])%p; 41 } 42 for (R i=0;i<=p;++i) 43 for (R j=1;j<=p;++j) 44 C[i][j]=(C[i][j-1]+C[i][j])%p; 45 } 46 47 ll c (ll n,ll m) 48 { 49 if(n<m) return 0; 50 return (f[n]*inv[m]%p)*inv[n-m]%p; 51 } 52 53 ll luc (ll n,ll m) 54 { 55 if(m==0) return 1; 56 else return (ll)luc(n/p,m/p)*c(n%p,m%p)%p; 57 } 58 59 int Lucas (ll n,ll k) 60 { 61 if(k<0) return 0; 62 if(n==0||k==0) return 1; 63 if(n<=p&&k<=p) 64 return C[n][k]; 65 return ((ll)C[n%p][p-1]*Lucas(n/p,k/p-1)%p+luc(n/p,k/p)*C[n%p][k%p]%p)%p; 66 } 67 68 int main() 69 { 70 scanf("%d",&T); 71 init(); 72 while (T--) 73 { 74 scanf("%lld%lld",&n,&k); 75 k=min(k,n); 76 printf("%d\n",Lucas(n,k)); 77 } 78 return 0; 79 }
---shzr



