数位dp
数位dp
数位dp难归难,可是NOIP考过呢。
$2^k$进制数:https://www.luogu.org/problemnew/show/P1066
题意概述:求解,满足:(1)是一个不少于两位的$2^k$进制数;(2)每一位严格小于右边那一位;(3)转换为2进制数后长度不超过w位;的$2^k$进制数有多少个。$1<=k<=9,k<w<=30000$
有一个组合数做法,但是这里就不讲了,找了asuldb的博客:$2^k$进制数
也有一个非常无脑的做法:以前做进制转换时都知道,一个$2^k$进制的数转换为二进制可以按位转换,一位变成k位。所以考虑用$dp[i][j]$表示第i位填了j的方案数,转移...还用说吗,转移时套上高精度,统计答案时注意最高位不要统计那些不合法的情况。

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # define R register int 5 6 using namespace std; 7 8 int k,w,x,r,maxx; 9 int dp[2][600][205]; 10 int ans[205]; 11 12 void add (int a[],int b[]) 13 { 14 int l=max(a[0],b[0])+2; 15 for (R i=1;i<=l;++i) 16 { 17 a[i]+=b[i]; 18 a[i+1]+=a[i]/10; 19 a[i]%=10; 20 } 21 while (a[l]==0&&l) l--; 22 a[0]=l; 23 } 24 25 int main() 26 { 27 scanf("%d%d",&k,&w); 28 x=w/k; 29 if(w%k) x++; 30 r=w-(x-1)*k; 31 maxx=(1<<k)-1; 32 for (R i=0;i<=maxx;++i) 33 dp[1][i][1]=dp[1][i][0]=1; 34 for (R i=2;i<=x;++i) 35 { 36 for (R j=maxx-1;j>=0;--j) 37 add(dp[i&1][j],dp[(i&1)^1][j+1]),add(dp[i&1][j],dp[i&1][j+1]); 38 if(i!=x) 39 for (R j=1;j<=maxx;++j) 40 add(ans,dp[i&1][j]); 41 else 42 for (R j=1;j<=(1<<r)-1;++j) 43 add(ans,dp[i&1][j]); 44 memset(dp[(i&1)^1],0,sizeof(dp[(i&1)^1])); 45 } 46 while (ans[ ans[0] ]==0&&ans[0]) ans[0]--; 47 if(ans[0]==0) printf("0"); 48 for (int i=ans[0];i>=1;--i) 49 printf("%d",ans[i]); 50 return 0; 51 }
数字计数:https://www.lydsy.com/JudgeOnline/problem.php?id=1833
题意概述:求$[a,b]$范围内,每个数码出现过多少次;$a,b<=10^{12}$
最早做的时候照着题解写的,现在已经看不懂了,又按照自己的方式写了一次.
$f[i][j][k]$表示当前填到第$i$位,是否卡上界,是否有意义(填过非$0$数字)的数字个数,$g[n][i][j][k]$表示相同状态下$n$数码的出现次数.好像还是挺水的.

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # include <algorithm> 6 # include <cmath> 7 # define R register int 8 # define ll long long 9 10 using namespace std; 11 12 int a[15],h; 13 ll l,r; 14 ll f[15][2][2],g[10][15][2][2]; 15 ll ans[10]; 16 17 int dp (ll x) 18 { 19 int h=0,mea,kk; 20 while(x) 21 { 22 a[++h]=x%10; 23 x/=10; 24 } 25 for (R i=1;i<=h/2;++i) 26 swap(a[i],a[h-i+1]); 27 memset(f,0,sizeof(f)); 28 memset(g,0,sizeof(g)); 29 f[0][1][0]=1; 30 for (R i=0;i<h;++i) 31 for (R j=0;j<=1;++j) 32 for (R k=0;k<=1;++k) 33 { 34 if(!f[i][j][k]) continue; 35 for (R x=0;x<=9;++x) 36 { 37 if(j==1&&x>a[i+1]) continue; 38 if(j==1&&x==a[i+1]) kk=1; 39 else kk=0; 40 if(x==0&&k==0) mea=0; 41 else mea=1; 42 f[i+1][kk][mea]+=f[i][j][k]; 43 if(mea) 44 { 45 for (R n=0;n<=9;++n) 46 g[n][i+1][kk][mea]+=g[n][i][j][k]; 47 g[x][i+1][kk][mea]+=f[i][j][k]; 48 } 49 } 50 } 51 return h; 52 } 53 54 int main() 55 { 56 scanf("%lld%lld",&l,&r); 57 h=dp(r); 58 for (R i=0;i<=9;++i) 59 ans[i]+=g[i][h][0][1]+g[i][h][1][1]; 60 if(l!=0) 61 { 62 h=dp(l-1); 63 for (R i=0;i<=9;++i) 64 ans[i]-=(g[i][h][0][1]+g[i][h][1][1]); 65 } 66 for (R i=0;i<=9;++i) 67 printf("%lld ",ans[i]); 68 return 0; 69 }
手机号码:https://www.lydsy.com/JudgeOnline/problem.php?id=4521
题意概述:要求$L,R$区间内满足至少3个相邻的相同数字且不能同时出现8和4的数字的个数。$10^{10}<=L<=R<10^{11}$
显然枚举是不可以的,但是可以数位$dp$,思想非常简单,数组开的十分复杂,有一个非常坑的点就是如果$L$正好卡在下界上,再减一就不再是$11$位了,所以可以特判这种情况,此时仅处理右边界.
$dp[i][f4][f8][u][l][x][las]$表示目前填到了第$i$位,是否出现过$4$,是否出现过$8$,是否卡上界,到上一位为止连续相同的数的长度,是否出现过长度大于$3$的连续序列,上一位填的是$las$的方案数,因为状态非常复杂,专转移的是否反而非常简单了.

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # define ll long long 5 # define R register int 6 7 using namespace std; 8 9 ll l,r,ans; 10 ll dp[13][2][2][2][2][4][10]; 11 int a[15]; 12 13 ll cal (ll maxn) 14 { 15 memset(dp,0,sizeof(dp)); 16 int len=0,f4,f8,fu,fh,le; 17 ll cnt=0; 18 while (maxn) 19 { 20 a[++len]=maxn%10; 21 maxn/=10; 22 } 23 for (R i=1;i<=len/2;++i) 24 swap(a[i],a[len-i+1]); 25 for (R i=0;i<=a[1];++i) 26 dp[1][i==4][i==8][i==a[1]][0][1][i]=1; 27 for (R i=1;i<11;++i) 28 for (R n4=0;n4<=1;++n4) 29 for (R n8=0;n8<=1;++n8) 30 { 31 if(n4&&n8) continue; 32 for (R u=0;u<=1;++u) 33 for (R h=0;h<=1;++h) 34 for (R lg=1;lg<=3;++lg) 35 for (R las=0;las<=9;++las) 36 { 37 if(!dp[i][n4][n8][u][h][lg][las]) continue; 38 for (R x=0;x<=9;++x) 39 { 40 if(u&&x>a[i+1]) continue; 41 f4=n4,f8=n8; 42 if(x==4) f4=1; 43 if(x==8) f8=1; 44 if(f4&&f8) continue; 45 if(u&&x==a[i+1]) fu=1; 46 else fu=0; 47 fh=h; 48 if(x==las) le=lg+1; 49 else le=1; 50 if(le>=3) le=3,fh=1; 51 dp[i+1][f4][f8][fu][fh][le][x]+=dp[i][n4][n8][u][h][lg][las]; 52 } 53 } 54 } 55 for (R n4=0;n4<=1;++n4) 56 for (R n8=0;n8<=1;++n8) 57 { 58 if(n4&&n8) continue; 59 for (R u=0;u<=1;++u) 60 for (R lg=1;lg<=3;++lg) 61 for (R x=0;x<=9;++x) 62 cnt+=dp[11][n4][n8][u][1][lg][x]; 63 } 64 return cnt; 65 } 66 67 int main() 68 { 69 scanf("%lld%lld",&l,&r); 70 if(l==1e10) l++,ans=cal(r)-cal(l-1)+1; 71 else ans=cal(r)-cal(l-1); 72 printf("%lld",ans); 73 return 0; 74 }
同类分布:https://www.lydsy.com/JudgeOnline/problem.php?id=1799
题意概述:求$[a,b]$中各位数字之和能整除原数的数的个数.$a,b<=10^{18}$
乍一看好像很难,但是可以发现这个各位数字之和不会很大,至多不过每个数都是$9$,也就是$162$,所以可以...枚举这个数字,数位$dp$求出有多少个数满足各位数字之和等于枚举的答案,且被这个数整除即可.时间复杂度$O(162^3 \times len \times 9$,看起来好像是一个不能过的复杂度,但是废状态非常多,实际上跑的飞快.
优化的方法:
1.不要一上来就直接枚举到$162$,而是先看一下最大的数有多少位,这个优化可以用来卡最优解,但是对于极限数据应该是没有什么差别的.($bzoj$所有数据共享时限所以也可以用一下)
2.第二维枚举数位和时只枚举到$min$(当前$check$的答案,位数$\times 9$)即可。
3.采用刷表法做$dp$,发现一个状态的值为$0$时直接$continue$,这个优化的效果简直像优化了复杂度一样好用,而且也是最好想最好写的,建议所有的数位$dp$都这么做.
4.这是一个比较赖皮的方法...但是对于大多数数位dp都有用:https://35178.blog.luogu.org/solution-p4127

1 // luogu-judger-enable-o2 2 # include <cstdio> 3 # include <iostream> 4 # include <cstring> 5 # define R register int 6 7 using namespace std; 8 9 long long a,b,B; 10 long long dp[20][163][163][2]; 11 long long ans=0; 12 int s=0; 13 14 long long coun (long long A,int s) 15 { 16 int len=0,c[20]={0},kk; 17 long long las; 18 memset(dp,0,sizeof(dp)); 19 while (A) 20 { 21 c[++len]=A%10; 22 A/=10; 23 } 24 for (R i=1;i<=len/2;++i) 25 swap(c[i],c[len-i+1]); 26 dp[0][0][0][1]=1; 27 for (R i=0;i<len;++i) 28 for (R j=0;j<=min(s,i*9+9);++j) 29 for (R z=0;z<=s;++z) 30 for (R k=0;k<=1;++k) 31 { 32 if(!dp[i][j][z][k]) continue; 33 las=dp[i][j][z][k]; 34 for (R x=0;x<=9;++x) 35 { 36 if(k&&x>c[i+1]) break; 37 if(k&&x==c[i+1]) kk=1; 38 else kk=0; 39 dp[i+1][j+x][(z*10+x)%s][kk]+=las; 40 } 41 } 42 return dp[len][s][0][0]+dp[len][s][0][1]; 43 } 44 45 int main() 46 { 47 scanf("%lld%lld",&a,&b); 48 B=b; 49 while (B) s+=9,B/=10; 50 for (R i=1;i<=min(s,162);++i) 51 { 52 ans+=coun(b,i); 53 ans-=coun(a-1,i); 54 } 55 printf("%lld",ans); 56 return 0; 57 }
windy数:https://www.lydsy.com/JudgeOnline/problem.php?id=1026
题意概述:不含前导零且相邻两个数字之差至少为2的正整数被称为windy数,$[a,b]$间的$windy$数.
一眼看上去像模板题,但是这个前导$0$好像挺麻烦的样子,因为如果前面都是$0$就不用考虑相邻数的那个限制,所以怎么办呢?把它一并开进状态里不就好了?

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # define R register int 6 # define ll long long 7 8 using namespace std; 9 10 long long a,b; 11 long long dp[11][10][2][2],t,ans; 12 int f[11],len,nu,nm; 13 14 int ab (int x) { if(x<0) return -x; return x; } 15 16 ll solve (ll x) 17 { 18 len=0; 19 while (x) 20 { 21 f[++len]=x%10; 22 x/=10; 23 } 24 for (R i=1;i<=len/2;++i) 25 swap(f[i],f[len-i+1]); 26 memset(dp,0,sizeof(dp)); 27 dp[0][0][1][0]=1; 28 for (R i=0;i<len;++i) 29 for (R las=0;las<=9;++las) 30 for (R u=0;u<=1;++u) 31 for (R m=0;m<=1;++m) 32 { 33 if(!dp[i][las][u][m]) continue; 34 t=dp[i][las][u][m]; 35 for (R n=0;n<=9;++n) 36 { 37 if(ab(n-las)<2&&m) continue; 38 if(u&&n>f[i+1]) continue; 39 if(u&&n==f[i+1]) nu=1; 40 else nu=0; 41 if(m==0&&n==0) nm=0; 42 else nm=1; 43 dp[i+1][n][nu][nm]+=t; 44 } 45 } 46 long long ans=0; 47 for (R las=0;las<=9;++las) 48 for (R k=0;k<=1;++k) 49 ans+=dp[len][las][k][1]; 50 return ans; 51 } 52 53 int main() 54 { 55 scanf("%lld%lld",&a,&b); 56 ans=solve(b)-solve(a-1); 57 printf("%lld",ans); 58 return 0; 59 }
在刷水题中找到了快乐(*^▽^*).
不要62:https://loj.ac/problem/10167
题意概述;区间$[l,r]$中不出现连续的$62$,不出现$4$的数字个数.
记得刚来高中部时老师给我们考了这道题,留下了深刻的印象,现在一看...水题啊.
$dp[i][j][k]$表示目前填到了第$i$位,卡不卡上界,上一位是不是$6$.转移时注意不能用$4$即可.

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # define R register int 5 6 using namespace std; 7 8 int l,r,dp[8][2][2],a[10],h; 9 10 int ask (int x) 11 { 12 int u; 13 h=0; 14 while (x) 15 { 16 a[++h]=x%10; 17 x/=10; 18 } 19 for (R i=1;i<=h/2;++i) 20 swap(a[i],a[h-i+1]); 21 memset(dp,0,sizeof(dp)); 22 dp[0][1][0]=1; 23 for (R i=0;i<h;++i) 24 for (R j=0;j<=1;++j) 25 for (R k=0;k<=1;++k) 26 { 27 if(!dp[i][j][k]) continue; 28 for (R n=0;n<=9;++n) 29 { 30 if(n==4) continue; 31 if(j==1&&n>a[i+1]) continue; 32 if(k&&n==2) continue; 33 if(j==1&&n==a[i+1]) u=1; 34 else u=0; 35 dp[i+1][u][n==6]+=dp[i][j][k]; 36 } 37 } 38 return dp[h][1][1]+dp[h][1][0]+dp[h][0][1]+dp[h][0][0]; 39 } 40 41 int main() 42 { 43 scanf("%d%d",&l,&r); 44 while (l||r) 45 { 46 printf("%d\n",ask(r)-ask(l-1)); 47 scanf("%d%d",&l,&r); 48 } 49 return 0; 50 }
数字游戏:https://loj.ac/problem/10164
题意概述:求区间$[l,r]$中满足各位数字从高到低不降的数字个数.
再这样刷水题就要退役了啊!
$dp[i][j][k]$表示目前填到第$i$位,卡不卡上界,上一位是什么.

1 # include <cstdio> 2 # include <iostream> 3 # include <queue> 4 # include <cstring> 5 # include <string> 6 # define R register int 7 # define ll long long 8 9 using namespace std; 10 11 int l,r,dp[12][2][10],a[15],h; 12 13 int ask (int x) 14 { 15 h=0; 16 int u; 17 while (x) 18 { 19 a[++h]=x%10; 20 x/=10; 21 } 22 for (R i=1;i<=h/2;++i) 23 swap(a[i],a[h-i+1]); 24 memset(dp,0,sizeof(dp)); 25 dp[0][1][0]=1; 26 for (R i=0;i<h;++i) 27 for (R j=0;j<=1;++j) 28 for (R las=0;las<=9;++las) 29 { 30 if(!dp[i][j][las]) continue; 31 for (R x=las;x<=9;++x) 32 { 33 if(j&&x>a[i+1]) continue; 34 if(j&&x==a[i+1]) u=1; 35 else u=0; 36 dp[i+1][u][x]+=dp[i][j][las]; 37 } 38 } 39 int ans=0; 40 for (R i=0;i<=1;++i) 41 for (R j=0;j<=9;++j) 42 ans+=dp[h][i][j]; 43 return ans; 44 } 45 46 int main() 47 { 48 while(scanf("%d%d",&l,&r)!=EOF) 49 printf("%d\n",ask(r)-ask(l-1)); 50 return 0; 51 }
数字游戏2:https://loj.ac/problem/10166
为什么一本通什么水题都往里收啊.

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # define R register int 6 7 using namespace std; 8 9 int a,b,n,u; 10 int dp[11][2][100]; 11 int f[11],h; 12 13 int ask (int x) 14 { 15 memset(dp,0,sizeof(dp)); 16 h=0; 17 while (x) 18 { 19 f[++h]=x%10; 20 x/=10; 21 } 22 for (R i=1;i<=h/2;++i) 23 swap(f[i],f[h-i+1]); 24 dp[0][1][0]=1; 25 for (R i=0;i<h;++i) 26 for (R j=0;j<=1;++j) 27 for (R m=0;m<n;++m) 28 { 29 if(!dp[i][j][m]) continue; 30 for (R x=0;x<=9;++x) 31 { 32 if(j&&x>f[i+1]) continue; 33 if(j&&x==f[i+1]) u=1; 34 else u=0; 35 dp[i+1][u][(m+x)%n]+=dp[i][j][m]; 36 } 37 } 38 return dp[h][0][0]+dp[h][1][0]; 39 } 40 41 int main() 42 { 43 while (scanf("%d%d%d",&a,&b,&n)!=EOF) 44 { 45 if(a>b) swap(a,b); 46 printf("%d\n",ask(b)-ask(a-1)); 47 } 48 return 0; 49 }
恨$7$不成妻:https://loj.ac/problem/10168
题意概述:求$[a,b]$中数位中不含$7$,数字和不整除$7$,整个数字不整除$7$的数的平方和$\%1000000007$;
我以为又可以开心的水一道水题了,然而被水题给水了.学数位$dp$的时候怎么不知道还有平方和这种操作啊?
然而想了一下发现并不是特别困难,是一道非常可做的题目.考虑一般做取模数位$dp$题时的转移方法,可以想到记录一些信息使得可以从上一位推到下一位。依旧使用$dp[i][j][k][z]$表示这个状态下的数字个数,$s[i][j][k][z]$表示填到$i$位时所有满足条件数字的和,$ss[i][j][k][z]$表示平方和.关于转移,$dp$数组的转移和平时没有什么差别,$s$数组是之前所有满足条件的数(设为$a_i$)的和,那么转移过来就是$\sum a_i \times 10+x$,这里$x$的个数就是$dp$转移过来的值.关于$ss$,新的$ss$应当等于
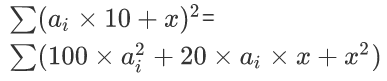
,可以用$dp$,$s$,$ss$三个数组的旧值进行更新.

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # include <cmath> 6 # include <algorithm> 7 # define R register int 8 # define ll long long 9 # define mod 1000000007 10 11 using namespace std; 12 13 ll dp[20][2][7][7],s[20][2][7][7],ss[20][2][7][7]; 14 ll l,r; 15 int a[20],T; 16 17 int ad (int a,int b) { a+=b; if(a>=mod) a-=mod; return a; } 18 19 ll ask (ll x) 20 { 21 memset(dp,0,sizeof(dp)); 22 memset(s,0,sizeof(s)); 23 memset(ss,0,sizeof(ss)); 24 dp[0][1][0][0]=1; 25 int u,h=0; 26 while (x) 27 { 28 a[++h]=x%10; 29 x/=10; 30 } 31 for (R i=1;i<=h/2;++i) swap(a[i],a[h-i+1]); 32 for (R i=0;i<h;++i) 33 for (R j=0;j<=1;++j) 34 for (R m_1=0;m_1<7;++m_1) 35 for (R m_2=0;m_2<7;++m_2) 36 { 37 if(!dp[i][j][m_1][m_2]) continue; 38 ll t=dp[i][j][m_1][m_2],ts=s[i][j][m_1][m_2],tss=ss[i][j][m_1][m_2]; 39 for (R x=0;x<=9;++x) 40 { 41 if(x==7) continue; 42 if(j&&x>a[i+1]) continue; 43 if(j&&x==a[i+1]) u=1; 44 else u=0; 45 dp[i+1][u][(m_1+x)%7][(m_2*10+x)%7]=ad(dp[i+1][u][(m_1+x)%7][(m_2*10+x)%7],t); 46 s[i+1][u][(m_1+x)%7][(m_2*10+x)%7]=ad(s[i+1][u][(m_1+x)%7][(m_2*10+x)%7],(10*ts+t*x)%mod); 47 ss[i+1][u][(m_1+x)%7][(m_2*10+x)%7]=ad(ss[i+1][u][(m_1+x)%7][(m_2*10+x)%7],(100*tss+20*ts*x+t*x*x)%mod); 48 } 49 } 50 ll ans=0; 51 for (R i=1;i<7;++i) 52 for (R j=1;j<7;++j) 53 ans=(ans+ss[h][0][i][j]+ss[h][1][i][j])%mod; 54 return ans; 55 } 56 57 int main() 58 { 59 scanf("%d",&T); 60 while(T--) 61 { 62 scanf("%lld%lld",&l,&r); 63 printf("%lld\n",(ask(r)-ask(l-1)+mod)%mod); 64 } 65 return 0; 66 }
--shzr


