倍增

倍增最广泛的应用就是求LCA了吧，反正我是从这里入坑的qwq

　　最近公共祖先：https://www.luogu.org/problemnew/show/P3379

  1 # include <cstdio>
  2 # include <iostream>
  3 
  4 using namespace std;
  5 
  6 int f,n,m,s,x,xx,b,y,h=0;
  7 char c;
  8 int firs[500007]={0},dep[500007]={0},F[500007][22]={0};
  9 bool vis[500007]={0};
 10 
 11 struct edge
 12 {
 13     int y;
 14     int Nex;
 15 }g[1000007]={0};
 16 
 17 int readd()
 18 {
 19     xx=0,f=1;
 20     c=getchar();
 21     while (! isdigit(c))
 22     {
 23         if(c=='-') f=-f;
 24         c=getchar();
 25     }
 26     while (isdigit(c))
 27     {
 28         xx=(xx<<3)+(xx<<1)+(c^48);
 29         c=getchar();
 30     }
 31     return xx*f;
 32 }
 33 
 34 void add(int x,int y)
 35 {
 36     g[++h].y=y;
 37     g[h].Nex=firs[x];
 38     firs[x]=h;
 39 }
 40 
 41 void build(int x)
 42 {
 43     for (int i=firs[x];i;i=g[i].Nex)
 44     {
 45         int j=g[i].y;
 46         if(!vis[j])
 47         {
 48             dep[j]=dep[x]+1;
 49             F[j][0]=x;
 50             vis[j]=true;
 51             for (int z=1;z<=21;z++)
 52               F[j][z]=F[ F[j][z-1] ][z-1];
 53             build(j);
 54         }
 55     }
 56 }
 57 
 58 int flca(int x,int y)
 59 {
 60     if(dep[x]>dep[y])
 61       swap(x,y);
 62     for (int i=20;i>=0;i--)
 63     {
 64         if(dep[x]<=dep[y]-(1<<i))
 65           y=F[y][i];
 66     }
 67     if(x==y) return x;
 68     for (int i=20;i>=0;i--)
 69     {
 70         if(F[x][i]==F[y][i])
 71           continue;
 72         x=F[x][i];
 73         y=F[y][i];
 74     }
 75     return F[x][0];
 76 }
 77 
 78 int main()
 79 {
 80     n=readd();
 81     m=readd();
 82     s=readd();
 83     for (int i=1;i<n;i++)
 84     {
 85         x=readd();
 86         y=readd();
 87         add(x,y);
 88         add(y,x);
 89     }
 90     dep[s]=1;
 91     vis[s]=true;
 92     build(s);
 93     for (int i=1;i<=m;i++)
 94     {
 95         x=readd();
 96         y=readd();
 97         printf("%d\n",flca(x,y));
 98     }
 99     return 0;
100 }

倍增求LCA

　　跑路：https://www.luogu.org/problemnew/show/P1613

　　货车运输：https://www.luogu.org/problemnew/show/P1967

　　题意概述：最大瓶颈路。

　　当时做的时候可没有听说过这么简单又清晰的名词。

　　发现这个图中有很多边是没有用的，因为不要求什么总路程最小之类的加法操作，只是取min，那么可以没有任何顾虑的绕很多路，也就是说，如果两个点之间有一条最小值为10的要绕好多别的点的路，它也是比直接相连的一条限重为5的路要优的，有没有想到什么算法呢？最小生成树。不过这道题是最大生成树。想到这个之后就非常简单了，只不过是在求lca的时候顺便维护一下最小值就行了。也可以用Kruscal重构树，也不错。

  1 // luogu-judger-enable-o2
  2 # include <cstdio>
  3 # include <iostream>
  4 # include <algorithm>
  5 # include <cmath>
  6 # define R register
  7 
  8 using namespace std;
  9 
 10 struct edge
 11 {
 12     int x,y,cos;
 13     int Nex;    
 14 };
 15 
 16 struct L
 17 {
 18     int lc,ma;
 19 };
 20 
 21 int szr,dep[10005]={0},firs[10005]={0},f[10005]={0};
 22 int Max,j,m,n,x,y,xx,ff,fx,fy,q,h=0;
 23 char cc;
 24 bool vis[10005]={false};
 25 edge a[50005],g[20010];
 26 L F[10005][14]={0};
 27 
 28 int father (int x)
 29 {
 30     if(x!=f[x]) return f[x]=father(f[x]);
 31     return x;
 32 }
 33 
 34 int readd()
 35 {
 36     xx=0;
 37     ff=1;
 38     cc=getchar();
 39     while (!isdigit(cc))
 40     {
 41         ff=-ff;
 42         cc=getchar();
 43     }
 44     while (isdigit(cc))
 45     {
 46         xx=(xx<<3)+(xx<<1)+(cc^48);
 47         cc=getchar();
 48     }
 49     return xx*ff;
 50 }
 51 
 52 bool cmp(edge a,edge b)
 53 {
 54     return a.cos>b.cos;
 55 }
 56 
 57 void add(int x,int y,int cos)
 58 {
 59     g[++h].y=y;
 60     g[h].cos=cos;
 61     g[h].Nex=firs[x];
 62     firs[x]=h;
 63 }
 64 
 65 void build(int x)
 66 {
 67     for (R int i=firs[x];i;i=g[i].Nex)
 68     {
 69         j=g[i].y;
 70         if(!vis[j])
 71         {
 72             dep[j]=dep[x]+1;
 73             vis[j]=true;
 74             F[j][0].lc=x;
 75             F[j][0].ma=g[i].cos;
 76             for (R int z=1;z<=13;z++)
 77             {
 78                 F[j][z].ma=min(F[j][z-1].ma,F[F[j][z-1].lc][z-1].ma);
 79                 F[j][z].lc=F[ F[j][z-1].lc ][z-1].lc;
 80             }
 81             build(j);  
 82         }
 83     }
 84 }
 85 
 86 int lca(int x,int y)
 87 {
 88     if(dep[x]>dep[y])
 89       swap(x,y);
 90     for (R int i=13;i>=0;i--)
 91       if(dep[x]<=dep[y]-(1<<i))
 92         y=F[y][i].lc;
 93     if(x==y) return x;
 94     for (R int i=13;i>=0;i--)
 95       if(F[x][i].lc==F[y][i].lc)
 96         continue;
 97       else
 98       {
 99           x=F[x][i].lc;
100           y=F[y][i].lc;
101       }
102     return F[x][0].lc;
103 }
104 
105 int lma(int x,int c)
106 {
107     Max=100009;
108     for (R int i=13;i>=0;i--)
109     {
110         if(dep[c]<=dep[x]-(1<<i))
111         {
112             Max=min(Max,F[x][i].ma);
113             x=F[x][i].lc;
114         }
115     }
116     return Max;
117 }
118 
119 int main()
120 {
121     n=readd();
122     m=readd();
123     for (R int i=1;i<=n;i++)
124       f[i]=i;
125     for (R int i=1;i<=m;i++)
126     {
127         a[i].x=readd();
128         a[i].y=readd();
129         a[i].cos=readd();
130     }
131     sort(a+1,a+1+m,cmp);
132     for (R int i=1;i<=m;i++)
133     {
134         fx=a[i].x;
135         fy=a[i].y;
136         fx=father(fx);
137         fy=father(fy);
138         if(fx!=fy)
139         {
140             f[fy]=fx;
141             add(a[i].x,a[i].y,a[i].cos);
142             add(a[i].y,a[i].x,a[i].cos);
143         }
144     }
145     for (R int i=1;i<=n;i++)
146       if(f[i]==i)
147       {
148           vis[i]=true;
149           dep[i]=1;
150           build(i);
151       }
152     q=readd();
153     for (R int i=1;i<=q;i++)
154     {
155         x=readd();
156         y=readd();
157         szr=lca(x,y);
158         if(szr==0)printf("-1\n");
159         else
160             printf("%d\n",min(lma(x,szr),lma(y,szr)));    
161     }
162     return 0;
163 }

货车运输

　　之前码风比较清奇，喜欢用id做变量名。后来还换了ID.

　　开车旅行：https://www.luogu.org/problemnew/show/P1081

　　题意概述：好麻烦，没法概述，看链接吧。

　　这个题预处理是最麻烦的，考虑逆序插入点，保证找到的点一定在给定点的东边，因为Set用的不大好，就种了一棵平衡树。最近的点一定是前驱或后继，如果最近的是前驱，那么第二近的可能是后继或者前驱的前驱，反之亦然。一定要注意处理好这个部分，如果不存在的话一定要写上-1，否则后面会麻烦。倍增部分：$id[i][j]$表示从$i$点走$2^j$步走到的点的编号，如果不存在就是-1；再定义两个数组分别对应$id$数组表示走这么远时A走了多少，B走了多少。写了一晚上...补充:做了$16$年的初赛题以后学到了一个新的技巧,用排序+链表实现本题中平衡树的功能,感觉挺有意思的:首先把每个点压进结构体,记录一下它的位置,排序后连成链表,从原位置最小的那个点开始找,因为它是最左边的,所以其他的点必然都在它的右边啦,找到它所需要的答案(也就是它的左右两个相连点)后把它删掉后再找第二个点的答案,显然这个时候是不会找到不合法解的,以此类推.

  1 # include <cstdio>
  2 # include <iostream>
  3 # include <set>
  4 # include <cstdlib>
  5 # include <map>
  6 # define inf 1000000009
  7 # define R register int
  8 
  9 using namespace std;
 10 
 11 const int maxn=100005;
 12 int n,X0,m,ans;
 13 int h[maxn],nex[maxn];
 14 int s[maxn],x[maxn],a[maxn],b[maxn];
 15 int id[maxn][18];
 16 long long al[maxn][18],bl[maxn][18];
 17 long long ansa,ansb,sa=0,sb=0;
 18 map <int,int> M;
 19 
 20 struct node
 21 {
 22     int n,r,v,s;
 23     node *ch[2];
 24     void in (int x)
 25     {
 26         v=x;
 27         n=s=1;
 28         r=rand();
 29         ch[0]=ch[1]=NULL;
 30     }
 31     int cmp (int x)
 32     {
 33         if(x==v) return -1;
 34         return x>v;
 35     }
 36     void update()
 37     {
 38         s=n;
 39         if(ch[0]) s+=ch[0]->s;
 40         if(ch[1]) s+=ch[1]->s;
 41     }
 42 }*roo,pool[maxn];
 43 
 44 node *newnode ()
 45 {
 46     static int cnt=0;
 47     return &pool[++cnt];
 48 }
 49 
 50 void rotate(node *&n,int d)
 51 {
 52     node *k=n->ch[d^1];
 53     n->ch[d^1]=k->ch[d];
 54     k->ch[d]=n;
 55     n->update();
 56     k->update();
 57     n=k;
 58 }
 59 
 60 void ins(node *&n,int x)
 61 {
 62     if(!n) n=newnode(),n->in(x);
 63     else
 64     {
 65         int d=n->cmp(x);
 66         if(d==-1) ++n->n;
 67         else
 68         {
 69             ins(n->ch[d],x);
 70             if(n->ch[d]->r > n->r)     rotate(n,d^1);
 71         }
 72         n->update();
 73     }    
 74 }
 75 
 76 int lef(node *&n,int x)
 77 {
 78     if(!n) return -inf;
 79     if(n->v>=x) return lef(n->ch[0],x);
 80     return max(n->v,lef(n->ch[1],x));
 81 }
 82 
 83 int rig(node *&n,int x)
 84 {
 85     if(!n) return inf;
 86     if(n->v<=x) return rig(n->ch[1],x);
 87     return min(n->v,rig(n->ch[0],x));
 88 }
 89 
 90 inline int read()
 91 {
 92     int x=0,f=1;
 93     char c=getchar();
 94     while (!isdigit(c)) { if(c=='-') f=-f; c=getchar();    }
 95     while (isdigit(c))  { x=(x<<3)+(x<<1)+(c^48); c=getchar(); }
 96     return x*f;
 97 }
 98 
 99 void init()
100 {
101     int l,r;
102     M[inf]=-1;
103     M[-inf]=-1;
104     M[inf+1]=-1;
105     M[-inf-1]=-1;
106     ins(roo,inf);
107     ins(roo,inf+1);
108     ins(roo,-inf);
109     ins(roo,-inf-1);
110     for (int i=n;i>=1;--i)
111     {
112         ins(roo,h[i]);
113         l=lef(roo,h[i]);
114         r=rig(roo,h[i]);
115         if(l<=-inf)
116         {
117             if(r>=inf) a[i]=b[i]=-1;
118             else
119             {
120                 b[i]=M[r];
121                 r=rig(roo,r);
122                 if(r<inf) a[i]=M[r];
123                 else a[i]=-1;
124             }
125         }
126         else
127         if(r>=inf)
128         {
129             if(l<=-inf) a[i]=b[i]=-1;    
130             else
131             {
132                 b[i]=M[l];
133                 l=lef(roo,l);
134                 if(l>-inf) a[i]=M[l];
135                 else a[i]=-1;
136             }
137         }
138         else
139         if(h[i]-l<=r-h[i])
140         {
141             b[i]=M[l];
142             l=lef(roo,l);
143             if(l<=-inf) a[i]=M[r];
144             else
145             if(h[i]-l<=r-h[i])
146                 a[i]=M[l];
147             else
148                 a[i]=M[r];
149         }
150         else
151         {
152             b[i]=M[r];
153             r=rig(roo,r);
154             if(r>=inf) a[i]=M[l];
155             else
156             if(h[i]-l<=r-h[i])
157                 a[i]=M[l];
158             else
159                 a[i]=M[r];
160         }
161     }
162 }
163 
164 int ab (int a)
165 {
166     if(a<0) return -a;
167     return a;
168 }
169 
170 void solve (int s,int x)
171 {
172     sa=sb=0;
173     long long Sum=0;
174     for (int i=17;i>=0;--i)
175     {
176         if(id[s][i]==-1) continue;
177         if(Sum+al[s][i]+bl[s][i]>x) continue;
178         Sum+=al[s][i]+bl[s][i];
179         sa+=al[s][i];
180         sb+=bl[s][i];
181         s=id[s][i];
182         if(s==-1) break;
183     }
184 }
185 
186 void bz()
187 {
188     for (int i=1;i<=n;++i)
189     {
190         id[i][0]=a[i];
191         if(a[i]==-1) 
192         {
193             id[i][1]=-1;
194             continue;    
195         }
196         al[i][0]=ab(h[i]-h[a[i]]);
197         bl[i][0]=0;
198         id[i][1]=b[ a[i] ];
199         if(id[i][1]==-1) continue;
200         al[i][1]=ab(h[i]-h[ a[i] ]);
201         bl[i][1]=ab(h[ a[i] ]-h[ b[ a[i] ] ]);
202     }
203     for (int i=n;i>=1;--i)
204         for (int j=2;j<=17;++j)
205         {
206             if(id[i][j-1]==-1) 
207             {
208                 id[i][j]=-1;
209                 continue;
210             }
211             id[i][j]=id[ id[i][j-1] ][j-1];
212             if(id[i][j]==-1) continue;
213             al[i][j]=al[ id[i][j-1] ][j-1]+al[i][j-1];
214             bl[i][j]=bl[ id[i][j-1] ][j-1]+bl[i][j-1];
215         }
216 }
217 
218 int main()
219 {
220     scanf("%d",&n);
221     for (R i=1;i<=n;++i)
222         h[i]=read(),M[ h[i] ]=i;
223     scanf("%d%d",&X0,&m);
224     for (R i=1;i<=m;++i)
225         s[i]=read(),x[i]=read();
226     init();
227     bz();
228     solve(1,X0);
229     ansa=sa;
230     ansb=sb;
231     ans=1;
232     for (R i=2;i<=n;++i)
233     {
234         solve(i,X0);
235         if(sb!=0)
236         {
237             if(sa*ansb<sb*ansa)
238             {
239                 ansa=sa;
240                 ansb=sb;
241                 ans=i;    
242             }
243             else if(sa*ansb==sb*ansa)
244             {
245                 if(h[ans]<h[i]) ans=i;
246             }
247         }
248         else
249         {
250             if(ansb!=0) continue;
251             else
252             {
253                 if(h[ans]<h[i]) ans=i;
254             }
255         }
256     }
257     printf("%d\n",ans);
258     for (R i=1;i<=m;++i)
259     {
260         solve(s[i],x[i]);
261         printf("%lld %lld\n",sa,sb);
262     }
263     return 0;
264 }

开车旅行

　　聚会:https://www.luogu.org/problemnew/show/P4281

　　题意概述:多组询问,给定无权树上三个点,找到一个点使得三点到这一点的总距离之和最小.$n,m<=500000$

　　今天考试考到了这个题，打表猜出了规律，现在尝试证明一下。　　

　　首先这个点肯定是某一对点的$LCA$,为什么呢?如果题目是问两个点,其中一个答案就是它们的$LCA$，扩展到三个点的情况：

　　看一看三点的$LCA$有多少种情况:开始随意指定$A,B$两点求出$LCA$,这时$C$点的放置有两种方法:1.接在$LCA$的子树内,那么它和$A$,$B$中至少一个的$LCA$还是之前那个$LCA$; 2.接在$LCA$的子树外面:那么它和$A,B$两点的$LCA$就是相同的了.事实上这两种情况没有太大差别,画出来都是这样子:

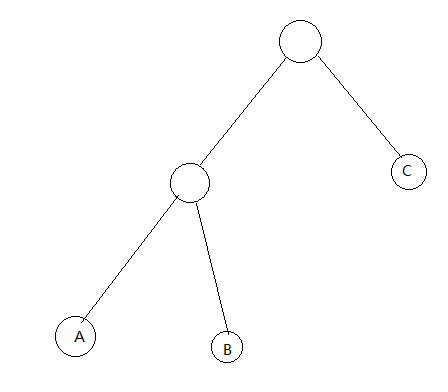
　　·三对$LCA$在同一点上,那么显然答案就是这个点,否则就会出现一个点的路程少了$X$,另两个点又各多了$X$的情况；

　　·$LCA$有两种位置：答案是深度更深的那个(也就是不同的那个),如果答案在它下面,那么有两个点要多走,不合理;如果答案在它上面,那么答案每上升一步,$A,B$两点就要多走一步，$C$却只能少走一步.

　　·$LCA$有三种取值：不存在；

　　注意卡常;

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cstring>
 4 # include <algorithm>
 5 # include <string>
 6 # include <cmath>
 7 # define R register int
 8 
 9 using namespace std;
10 
11 const int maxn=500005;
12 int n,m,x,y,l,a,b,c,h,firs[maxn],dep[maxn],f[maxn][21],ans,co,pos,l1,l2,l3,lg[maxn];
13 struct edge
14 {
15     int too,nex;
16 }g[maxn<<1];
17 
18 int read ()
19 {
20     int x=0;
21     char c=getchar();
22     while(!isdigit(c)) c=getchar();
23     while(isdigit(c)) { x=(x<<3)+(x<<1)+(c^48); c=getchar(); }
24     return x;
25 }
26 
27 void dfs (int x)
28 {
29     int j;
30     for (R i=firs[x];i;i=g[i].nex)
31     {
32         j=g[i].too;
33         if(dep[j]) continue;
34         dep[j]=dep[x]+1;
35         f[j][0]=x;
36         for (R k=1;k<=lg[ dep[j] ];++k)
37             f[j][k]=f[ f[j][k-1] ][k-1];
38         dfs(j);
39     }
40 }
41 
42 int lca (int x,int y)
43 {
44     if(dep[x]>dep[y]) swap(x,y);
45     for (R i=lg[ dep[y] ];i>=0;--i)
46         if(dep[y]-(1<<i)>=dep[x]) y=f[y][i];
47     if(x==y) return x;
48     for (R i=lg[ dep[x] ];i>=0;--i)
49     {
50         if(f[x][i]==f[y][i]) continue;
51         x=f[x][i];
52         y=f[y][i];
53     }
54     return f[x][0];
55 }
56 
57 int dis (int a,int b)
58 {
59     int l=lca(a,b);
60     return dep[a]+dep[b]-2*dep[l];
61 }
62 
63 void add (int x,int y)
64 {
65     g[++h].too=y;
66     g[h].nex=firs[x];
67     firs[x]=h;
68 }
69 
70 int main()
71 {
72     n=read(),m=read();
73     for (R i=2;i<=n;++i)
74         lg[i]=lg[i>>1]+1;
75     for (R i=1;i<n;++i)
76     {
77         x=read(),y=read();
78         add(x,y);
79         add(y,x);
80     }
81     dep[1]=1;
82     dfs(1);
83     for (R i=1;i<=m;++i)
84     {
85         a=read(),b=read(),c=read();
86         l1=lca(a,b);
87         l2=lca(a,c);
88         l3=lca(b,c);
89         if(l1==l2) l=l3,swap(a,c);
90         if(l2==l3) l=l1;
91         if(l1==l3) l=l2,swap(b,c);
92         printf("%d %d\n",l,dep[a]+dep[b]-2*dep[l]+dis(c,l));
93     }
94     return 0;
95 }

聚会

---shzr

posted @ 2018-08-23 21:55 shzr 阅读(304) 评论(0) 编辑收藏举报

刷新页面返回顶部

shzr

退役啦，去学文化课~

倍增

公告