列队
好久没有写过单题的解题报告了呢!其实单题挺有意思的,可以随意的延伸,不用像写的别的博客那样怕跑题。
列队:https://www.luogu.org/problemnew/show/P3960
题面就不用说了吧。
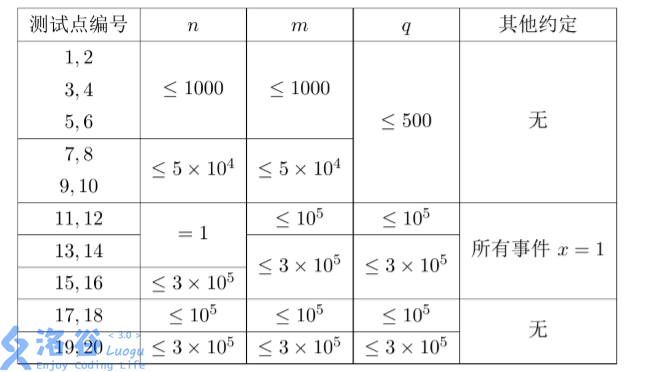
D2T3怎么可能写正解呢,不如愉快的研究部分分。NOIP的部分分向来是很足的,甚至到了正解与一堆暴力的拼凑就差10~20的地步,而且正解还有可能被卡常....(所以正解有什么用嘛)
1-6:怎么有这么多无脑模拟分呀...开个二维数组按照他的说法随便模拟模拟就OK啦。
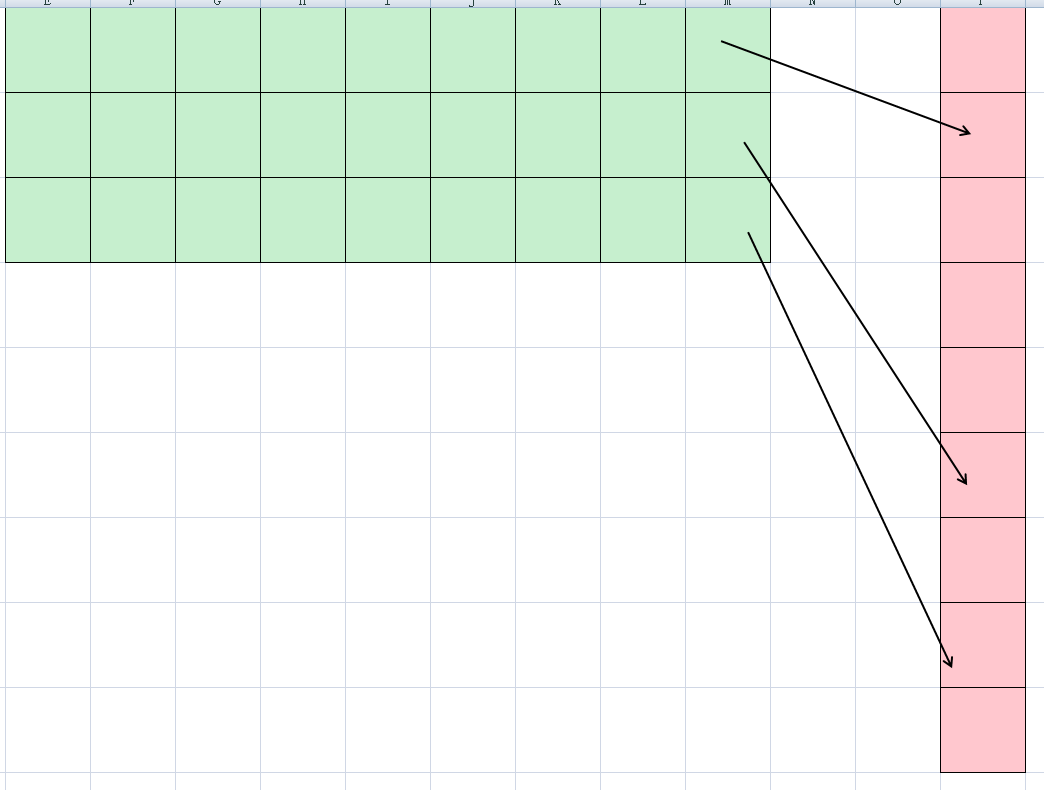
7-10:虽然n很大,但是有用的行只有500呢,可以每一行只考虑前(m-1)个,最后一列单独维护,来一张图感受一下:

绿色部分是有人离队的行,红色是最后一列,黄色就是没有什么用的格子。
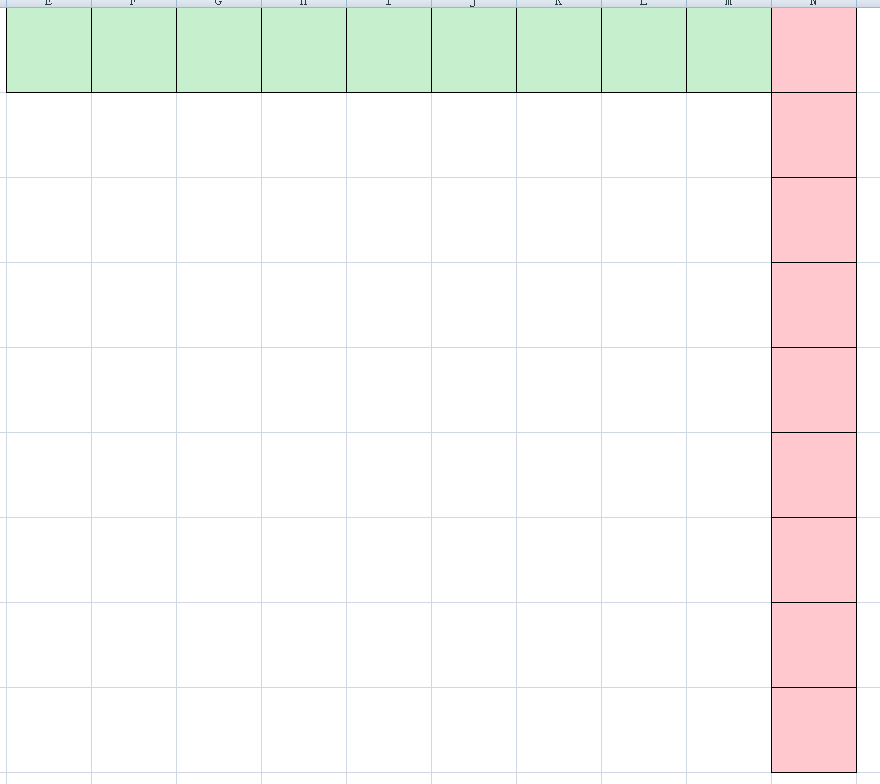
我们把它进行一番离散化:
这样离散化后,绿色部分的大小不会超过$q*m$,红色部分也只有$n$那么长,接下来就可以沿用刚刚的思路(模拟)来做,时间复杂度十分优越;
11-14:这里就有点难度啦,但是如果会平衡树的话就可以放弃思考,使用高级数据结构骗分。只有一行是什么意思呢?就是每次选出第k个数插入到最后,听起来一种浓浓的Treap气息,只需要:插入,删除,找第K大三个操作,再找一个比较大的数组存一下平衡树中每个结点的真实编号。

15-16:只有第一行有操作,看起来和离散化的部分分有异曲同工之妙,长这个样子:
这么一来就有两个思路啦,一个是横行一棵Treap,纵行一棵,但是很麻烦呀,还有一个方法就是把横行以交点为圆心逆时针旋转九十度拼成一个长的横行,按照之前的思路用用一棵就可以维护了。
17-20:不会。唯一的思路是每行开一个Treap,最后一列再来一个,但是空间直接爆炸啊。

1 # include <cstdio> 2 # include <iostream> 3 # include <cstdlib> 4 # include <iostream> 5 # include <cmath> 6 # include <algorithm> 7 # define R register int 8 9 int n,m,x,y,l,q; 10 int a_sim[1005][1005]; 11 long long b[1009],num[2000009],link[400009],a_link[502][50009]; 12 inline int min(int a,int b) { if(a<b) return a; return b; } 13 struct ask 14 { 15 int x,y; 16 }a[509]; 17 18 struct node 19 { 20 int n,v,s,r; 21 node *ch[2]; 22 void in (int x) 23 { 24 n=s=1; 25 v=x; 26 r=rand(); 27 ch[0]=ch[1]=NULL; 28 } 29 int cmp (int x) 30 { 31 if(x==v) return -1; 32 return x>v; 33 } 34 void update() 35 { 36 s=n; 37 if(ch[0]) s+=ch[0]->s; 38 if(ch[1]) s+=ch[1]->s; 39 } 40 }*roo,pool[2000009]; 41 42 node *newnode() 43 { 44 static int cnt=0; 45 return &pool[++cnt]; 46 } 47 48 void rotate (node *&n,int d) 49 { 50 node *k=n->ch[d^1]; 51 n->ch[d^1]=k->ch[d]; 52 k->ch[d]=n; 53 n->update(); 54 k->update(); 55 n=k; 56 } 57 58 void ins (node *&n,int x) 59 { 60 if(!n) n=newnode(),n->in(x); 61 else 62 { 63 int d=n->cmp(x); 64 if(d==-1) n->n++; 65 else 66 { 67 ins(n->ch[d],x); 68 if(n->ch[d]->r > n->r) rotate(n,d^1); 69 } 70 n->update(); 71 } 72 } 73 74 int value (node *&n,int x) 75 { 76 if(!n||n->s<x||x<=0) return 0; 77 int s=n->ch[0]?n->ch[0]->s:0; 78 if(s+1<=x&&x<=s+n->n) return n->v; 79 if(s>=x) return value(n->ch[0],x); 80 return value(n->ch[1],x-s-n->n); 81 } 82 83 void del (node *&n,int x) 84 { 85 if(!n) return; 86 int d=n->cmp(x); 87 if(d==-1) 88 { 89 if(n->n > 1) n->n--; 90 else 91 { 92 if(!n->ch[1]) n=n->ch[0]; 93 else if(!n->ch[0]) n=n->ch[1]; 94 else 95 { 96 int f=(n->ch[0]->r > n->ch[1]->r)?1:0; 97 rotate(n,f); 98 del(n->ch[f],x); 99 } 100 } 101 }else del(n->ch[d],x); 102 if(n) n->update(); 103 } 104 105 void cheat_sim() 106 { 107 for (R i=1;i<=n;++i) 108 for (R j=1;j<=m;++j) 109 a_sim[i][j]=(i-1)*m+j; 110 for (R i=1;i<=q;++i) 111 { 112 scanf("%d%d",&x,&y); 113 l=a_sim[x][y]; 114 printf("%d\n",l); 115 for (R j=y;j<=m;++j) 116 a_sim[x][j]=a_sim[x][j+1]; 117 for (R j=x;j<=n;++j) 118 a_sim[j][m]=a_sim[j+1][m]; 119 a_sim[n][m]=l; 120 } 121 } 122 123 void cheat_line() 124 { 125 for (R i=1;i<=m;++i) 126 num[i]=i,ins(roo,i); 127 int cnt=m,ans; 128 for (R i=1;i<=q;++i) 129 { 130 scanf("%d%d",&x,&x); 131 ans=value(roo,x); 132 del(roo,ans); 133 printf("%lld\n",num[ans]); 134 num[++cnt]=num[ans]; 135 ins(roo,cnt); 136 } 137 } 138 139 void cheat_link() 140 { 141 for (R i=1;i<=m;++i) 142 num[i]=i,ins(roo,i); 143 for (R i=2;i<=n;++i) 144 num[i+m-1]=(long long)i*m,ins(roo,i+m-1); 145 int ans,cnt=n+m-1; 146 for (R i=1;i<=q;++i) 147 { 148 scanf("%d%d",&x,&x); 149 ans=value(roo,x); 150 del(roo,ans); 151 printf("%lld\n",num[ans]); 152 num[++cnt]=num[ans]; 153 ins(roo,cnt); 154 } 155 } 156 157 void cheat_ls() 158 { 159 for (int i=1;i<=q;++i) 160 scanf("%d%d",&a[i].x,&a[i].y),b[i]=a[i].x; 161 std::sort(b+1,b+1+q); 162 int tot=std::unique(b+1,b+q+1)-b-1; 163 for(int i=1;i<=q;i++) 164 { 165 int t=a[i].x; 166 a[i].x=std::lower_bound(b+1,b+tot+1,a[i].x)-b; 167 num[ a[i].x ]=t; 168 } 169 for (int i=1;i<=q;++i) 170 for (int j=1;j<m;++j) 171 a_link[i][j]=(long long)(num[i]-1)*m+j; 172 for (int i=1;i<=n;++i) 173 link[i]=i*m; 174 for (int i=1;i<=q;++i) 175 { 176 int h=a[i].x; 177 long long ans; 178 if(a[i].y!=m) 179 ans=a_link[h][ a[i].y ]; 180 else 181 ans=link[ h ]; 182 printf("%lld\n",ans); 183 for (int j=a[i].y;j<m-1;++j) 184 a_link[h][j]=a_link[h][j+1]; 185 a_link[h][m-1]=link[ num[h] ]; 186 for (int j=num[h];j<n;++j) 187 link[j]=link[j+1]; 188 link[n]=ans; 189 } 190 } 191 192 int main() 193 { 194 scanf("%d%d%d",&n,&m,&q); 195 if(n<=1000&&m<=1000) cheat_sim(); 196 else if(n==1) cheat_line(); 197 else if(q<=500) cheat_ls(); 198 else cheat_link(); 199 return 0; 200 }
想了一下决定还是学一下正解思路,发现正解的思路太神啦!
首先每次有人出队后整个方阵都会是形如这个样子的:(绿色:原先就在这个行上的人;红色:后来对齐到这一行的人; 蓝色:最后一列)

对于每行开一个平衡树/线段树/树状数组看起来都不可行,然而看了多篇题解后,我发现这三个思路稍加改进竟然都可行,每个都挺妙的,各显神通...
·讲起来最简单,实现起来却并不简单的平衡树思路:
因为出队的总共只有q个人,考虑根据这个来做,所以可以用平衡树维护一段连续的区间,每当要从区间里删数的时候就把区间断成三块,把中间的删掉,插入到最后一列里,从最后一列里找到第X(行数)个人扔进这一行里面。听起来确实挺简单的,不过带分裂的平衡树想想就难写...
·不算难想,听说也不难写的线段树思路:
权值线段树,动态开点,除此之外和上边一样。
·非常难想,也并不好写的树状数组思路:
为什么我要学这个呢...当时看到树状数组觉得比平衡树简单,就学了这个做法,但是现在想想,同一道题肯定还是用复杂的数据结构好做啊...
听说这是官方给出的标算。先概括一下思路:首先求出每次出队的人是这一行中第几个曾经来过的人,把他拿出来,找到最后一列的第x个人放进这一行,刚刚拿出来的人放到最后一列。
用一种类似于权值树状数组的东西来维护每行第K个数,因为时间过得去就不记录size了,用二分来查找第K个数,数组要开到m+q那么大。欸,那这样不是超空间更厉害了吗?这里就有一些神奇的方法了,离线!如果不考虑最后一列,每行之间是不是完全没有影响呢?答案是肯定的,所以可以分行离线做,用同一个树状数组,对于行数相同的离队申请按照出现的次序排序即可。注意如果出队的是最后一列的人,跳过他不要考虑,否则会把数组弄乱了。一个非常神奇又非常科学的优化:不要做每一行的时候都清空一次树状数组再初始化,这样复杂度就退化到$N*M*log(m+q)$了,正确做法是每次记录这一行在哪些节点处进行过删除,做完这一行之后再加回来就行了,看起来好像差别不大,但是因为一共只有q个出队的人,一共也只可能删q次,加q次,显得非常合理。
对于所有的询问再按出现次序排排序,开始作答。现在的问题是,我们知道每次出队的是这一行的第几个人了,但是怎么知道他的序号是什么呢?如果是前m个还好说,算一下就可以了,但是超过的怎么办呢?解决方法非常C++,开n个vector,每次加入这一行的,超过m的人扔进vector里面,虽然看着是一个很大的二维数组,但是依然一共只有q个...
最后一列的第X个人的寻找方法同上,超过的人的编号问题同上,再开一个vector解决一切问题。这么说来也不算难,不过考场上可能不大好想吧。

1 # include <iostream> 2 # include <cstdio> 3 # include <vector> 4 # include <queue> 5 # include <algorithm> 6 # define lowbit(i) ((i)&(-i)) 7 8 using namespace std; 9 10 const int maxn=3*100009; 11 vector <long long> a[maxn],b; 12 queue <int> del; 13 int n,m,q,t[maxn<<1],siz,mx; 14 long long las; 15 struct ask 16 { 17 int x,y,rk,pre; 18 }Q[maxn]; 19 20 bool cmp (ask a,ask b) 21 { 22 if(a.x!=b.x) return a.x<b.x; 23 return a.rk<b.rk; 24 } 25 26 bool cmp2 (ask a,ask b) 27 { 28 return a.rk<b.rk; 29 } 30 31 void add (int x,int v) 32 { 33 for (int i=x;i<=mx;i+=lowbit(i)) 34 t[i]+=v; 35 } 36 37 int ask (int x) 38 { 39 int ans=0; 40 for (int i=x;i;i-=lowbit(i)) 41 ans+=t[i]; 42 return ans; 43 } 44 45 int Find (int k) 46 { 47 int l=0,r=mx; 48 int mid,ans; 49 while(l<=r) 50 { 51 mid=l+r>>1; 52 if(ask(mid)>=k) ans=mid,r=mid-1; 53 else l=mid+1; 54 } 55 return ans; 56 } 57 signed main() 58 { 59 cin>>n>>m>>q; 60 mx=max(n,m)+q; 61 for (int i=1;i<=q;++i) 62 scanf("%d%d",&Q[i].x,&Q[i].y),Q[i].rk=i; 63 sort(Q+1,Q+1+q,cmp); 64 int beg=Q[1].x,i=1; 65 for (int i=1;i<=mx;++i) 66 add(i,1); 67 while (i!=q+1) 68 { 69 while(Q[i].x==beg) 70 { 71 if(Q[i].y==m) 72 { 73 i++; 74 continue; 75 } 76 Q[i].pre=Find(Q[i].y); 77 add(Q[i].pre,-1); 78 del.push(Q[i].pre); 79 i++; 80 } 81 beg=Q[i].x; 82 while (del.size()) 83 add(del.front(),1),del.pop(); 84 } 85 sort(Q+1,Q+1+q,cmp2); 86 for (int i=1;i<=mx;++i) 87 t[i]=0; 88 for (int i=1;i<=mx;++i) 89 add(i,1); 90 for (int i=1;i<=q;++i) 91 { 92 las=Find( Q[i].x ); 93 add(las,-1); 94 if(las<=n) las=(long long)las*m; 95 else las=b[las-n-1]; 96 if(Q[i].y!=m) 97 { 98 a[ Q[i].x ].push_back(las); 99 if(Q[i].pre<m) las=(long long)(Q[i].x-1)*m+Q[i].pre; 100 else las=a[ Q[i].x ][ Q[i].pre-m ]; 101 } 102 b.push_back(las); 103 printf("%lld\n",las); 104 } 105 return 0; 106 }
感觉这道题是真的难...尤其是这个vector的部分对pascal选手以及不常用STL的选手是不是不大友好呀qwq
---shzr


