斜率优化dp

　　斜率优化dp

　　首先让我们来回顾一下：

　　这是我6.23说的：

　　

　　这是7.9说的：

　　

　　这是7.10说的：

　　

　　这是7.11说的：

　　

　　然后请回头看看本文的标题。好的。一个显然的事实是，我放飞自我了。直接原因是：NOIP历年真题会做的都做完了；根本原因是：学新的东西就是比较有意思。当然我可以找到数十个理由来解释我学新东西的合理性和必要性，但是真正的原因就是这个。

 　   不过PJ都开始考二分+单调队列dp了，TG考斜率也不是不可能的事情。(喜新厌旧的借口 1/1)

---

 

　　首先来看一道题目：

　　玩具装箱：https://www.lydsy.com/JudgeOnline/problem.php?id=1010

　　大概是一道斜率优化经典题，不过SC的时候rqy说也可以用四边形不等式优化。

　　尝试来概括一下一句话题意：

　　把一个长度为$N$的序列分成若干段并给定一个常数L，每段的代价是

　　

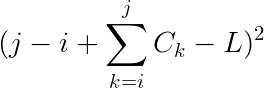
　　最小化这个代价。($1<=N<=50000$)

　　朴素的写法当然非常简单啦，就是一个N^2的类似于暴力的dp就可以，问题是它过不了啊...

　　这时候就要请出神奇的斜率优化啦！

　　把暴力的式子进行一番化简，把只跟$j$有关的放在右边,对于每一个S把她加一，L也加一，可以使式子简约一点。

　　

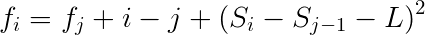
　　加一后  ---> 

　　

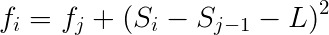
　　展开：

　　

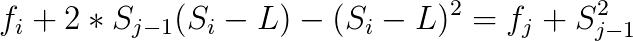
　　再进行一些非常有意思的替换。

　　   

　　然后上边那个式子就变成了非常简单的东西：

　　

　　是不是很像直线的方程呀。如果我们画一个点x,y并用一条斜率为k的直线穿过它，那它的截距也就可以算出来了，再减去$b$不就是$f_i$了吗！看起来非常巧妙。可是这有什么用呢？因为我们要求的是$f_i$的最小值，自然希望截距最小，斜率已经固定了，从下往上移动直线，碰到的第一个点就是答案啦。不想画图.jpg 回忆一下吧，想想课件上那张图，要维护的就是一个下凸壳(qiao？ke？)，还支持插入新的点，听起来好麻烦呀，其实就是很麻烦，但是我们可以利用一些好的性质，比如说本题中前缀和单调递增，也就是只会在最右边插入点，那么用一个单调队列就可以维护凸壳了，因为同样的原因，直线的斜率也是递增的，所以只有在最左边才会有点失效，同样使用单调队列即可。如果对精度要求还没有到丧心病狂的程度，建议还是算出斜率来再进行比较，而不要用那种十字相乘的方法，非常容易溢出。

　　推荐一个写的非常好的blog：https://www.luogu.org/blog/user35178/xie-shuai-you-hua

　　

# include <cstdio>
# include <iostream>
# include <cstring>

using namespace std;

const int maxn=50009;
int n,l,h=1,t=1;
int c[maxn];
long long s[maxn],dp[maxn];
int q[maxn];

long long X (int x) { return s[x]; }
long long Y (int x) { return s[x]*s[x]+dp[x]; }
long long B (int x) { return (long long)(s[x]-l)*(s[x]-l); }

double check ()
{
    int a=q[h],b=q[h+1];
    return (double)(Y(a)-Y(b))/(X(a)-X(b));   
}

void ins (int i)
{
    int a,b,c;
    a=q[t-1],b=q[t],c=i;
    while (t-h>0&&(X(c)-X(a))*(Y(b)-Y(a))>(X(b)-X(a))*(Y(c)-Y(a))) t--;
    q[++t]=i;
}

int main()
{
    scanf("%d%d",&n,&l);
    l++;
    for (int i=1;i<=n;++i)
        scanf("%d",&c[i]),c[i]=c[i]+1,s[i]=s[i-1]+c[i];
    for (int i=1;i<=n;++i)
    {
        while(t-h>0&&check()<2.0*(X(i)-l)) h++;
        dp[i]=Y(q[h])-2*(s[i]-l)*X(q[h])+B(i);
        ins(i);
    }
    printf("%lld",dp[n]);
    return 0;
}

 

 

　　征途：https://www.lydsy.com/JudgeOnline/problem.php?id=4518

　　wzx推荐的好题，他新改了ID，不过不是很好记：asuldb，随机出来的。

　　突然不想再写式子了qwq，明天再写。

　　题意概述：把一列长度为n的数划分成m段，每段合成一个数为总和，使得总方差最小，输出方差乘上$m^2$防止精度误差。$n<=3000$

　　也就是要求这个式子的最小值啦:

　　

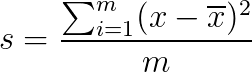
　　其实还是挺好做的，关键是化化式子：

　　

　　

　　

　　　

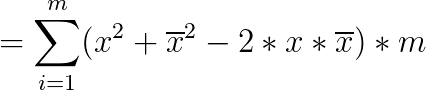
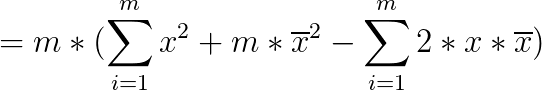
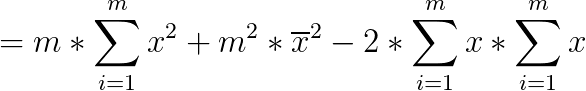
　　这时候我们发现了一件神奇的事情...上边那个式子减号后面就是一个常数了...不影响式子的取值，扔掉。

　　

　　

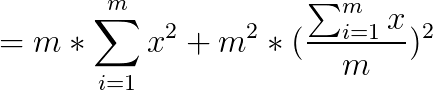
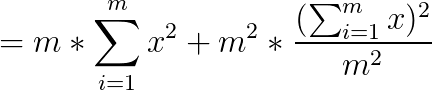
　　加号后边是一个常数，扔掉。

　　

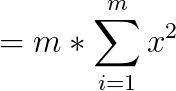
　　m是常数，扔掉。

　　

　　所以只有这个才是真正有用的东西。而且只和分段方法有关系，可以制作一个非常简单的dp。$dp[i][j]$表示前i个分成j段的最优值，怎么转移呢？

　　$dp[i][j]=min(dp[i][k]+(s[j]-s[k])^2)$

　　这是一个$N^3$的式子，显然是过不了的，但是斜率优化已经非常非常明显了。因为二维的dp不好改，所以考虑按层dp,因为每个$dp[i][x]$必然是由某一个$dp[j][x-1]$转移而来，所以每次只转移一层，套用斜率优化即可。

　　

# include <cstdio>
# include <iostream>
# include <cstring>

using namespace std;

int n,m,S;
int a[3009],s[3009];
long long dp[3009][3009];
int q[3009],h,t;

long long X (int i,int j) { return s[i]; }
long long Y (int i,int j) { return dp[i][j]+s[i]*s[i]; }

void ins (int i,int j)
{
    int a,b,c;
    if(h<t) a=q[t-1],b=q[t],c=i;
    while (h<t&&(double)(Y(b,j)-Y(a,j))/(X(b,j)-X(a,j))>(double)(Y(c,j)-Y(b,j))/(X(c,j)-X(b,j)))
    {
        t--;
        a=q[t-1],b=q[t],c=i;
    }
    q[++t]=i;
}

int main()
{
    memset(dp,0x3f,sizeof(dp));
    dp[0][0]=0;
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;++i)
        scanf("%d",&a[i]),s[i]=s[i-1]+a[i];
    for (int j=1;j<=m;++j)
    {
        h=1,t=0;
        for (int i=1;i<=n;++i)
        {
            ins(i-1,j-1);
            while (h<t&&(double)(Y(q[h+1],j-1)-Y(q[h],j-1))/(X(q[h+1],j-1)-X(q[h],j-1))<(double)2.0*s[i]) h++;
            dp[i][j]=dp[ q[h] ][ j-1 ]+(s[i]-s[ q[h] ])*(s[i]-s[ q[h] ]);
        }
    }
    printf("%lld",dp[n][m]*m-s[n]*s[n]);
    return 0;
}

　　从这道题上，我还学到了一种优化dp的方法，可以将任意dp优化到任意复杂度!惟一的小缺点是正确性可能就差了那么一点。因为这道题的斜率优化部分是拿单调队列实现的，但是我的单调队列中有一个除号写成了乘号，从而达成了几乎是随机从前面找一个状态进行转移的效果，却拿了70分，导致我一直以为是细节问题。这么看来，如果从前面随机选出$logN$,$\sqrt{N}$，那几乎就可以AC了...

　　

 

　　---shzr