搜索-2
搜索-2
搜索真是挺神的一个东西,即使是开了这个搜索-2还是不一定能说全。在这里就提前说好,这一篇比上一篇的难度大在剪枝,优化和保存状态,不涉及A*,IDA*,dancing links等毒瘤算法,如果有一天真的学了这些,就再开一篇搜索-3。(突然觉得不想再开了,就写在一起吧)
虫食算:https://www.luogu.org/problemnew/show/P1092
题意概述:n进制加法,所有字母代表的数都不知道,求出唯一的解。
既然什么都不知道。。。那就搜索吧。
40分:用全排列的思路搜索,搜完一组解再判断是否合法。
T到飞起。
70分:每搜出一个数就用它判断是否合法。
在n进制加法中,每一位的进位最多只有一位,如果当前abc的i位都已经确定了,但是无论是否进位都不合法的时候,return;
If(a[i]+b[i])%n!=c[i]&&(a[i]+b[i]+1)%n!=c[i] return false;
注意最高位不能再进位。
还是TLE。
100分:刚刚算法的瓶颈在于判断时没有方向,很可能判断一些还没有定数的情况而浪费时间,所以搜数顺序不能从$0$~$n-1$,而是用归并的思路,使得$a,b,c$的第$i$位尽量同时的被搜到,剪枝时就快了很多。
这样处理后再按照$s$数组的顺序搜数,结合可行性剪枝时$i$从$n-1$~$0$循环可以在判断时更早排除一些情况。
正解2:高斯消元:这个真的不会。

# include <cstdio> # include <iostream> # include <cstring> # include <string> # define R register int using namespace std; int n,a[30],b[30],c[30],s[30]; int h=-1,ans[30]; char x; int vis[30],met[30]; int che[30]; bool ff=false,f; void writ() { int r=0; for (R i=n-1;i>=0;i--) { if((ans[a[i]]+ans[b[i]]+r)%n!=ans[c[i]]) return ; r=(ans[a[i]]+ans[b[i]]+r)/n; } if (r) return ; for (R i=0;i<n-1;i++) printf("%d ",ans[i]); printf("%d",ans[n-1]); ff=true; } bool check() { if(ans[a[0]]+ans[b[0]]>=n) return false; int A,B,C; for (R i=n-1;i>=0;i--) { A=ans[a[i]]; B=ans[b[i]]; C=ans[c[i]]; if(A==-1||B==-1||C==-1) continue; if((A+B)%n!=C&&(A+B+1)%n!=C) return false; } return true; } void dfs(int x) { if(check()==false) return ; if(x==n) writ(); if (ff) return ; for (R i=n-1;i>=0;i--) { if(vis[i]) continue; ans[s[x]]=i; vis[i]=1; dfs(x+1); ans[s[x]]=-1; vis[i]=0; } } int main() { scanf("%d",&n); for (R i=0;i<n;i++) cin>>x,a[i]=x-'A'; for (R i=0;i<n;i++) cin>>x,b[i]=x-'A'; for (R i=0;i<n;i++) cin>>x,c[i]=x-'A'; for (R i=n-1;i>=0;i--) { if(vis[a[i]]==false) s[++h]=a[i],vis[a[i]]=1; if(vis[b[i]]==false) s[++h]=b[i],vis[b[i]]=1; if(vis[c[i]]==false) s[++h]=c[i],vis[c[i]]=1; if(h==n-1) break; } memset(vis,0,sizeof(vis)); for (R i=0;i<=n;i++) ans[i]=-1; dfs(0); return 0; }
生日蛋糕:https://www.luogu.org/problemnew/show/P1731
题意概述:制作一个$m$层,体积给定的蛋糕,使得表面积最小(底面不算),要求每一层的H,R比下面的一层的H,R小。
这题好神啊,以前看到这道题完全看不出来有什么好搜的,还觉得这道题能想到搜索实在太厉害了,后来才发现这个思路真的很暴力,没有我想象中那么神奇。
记得第一次做这个题趁中午到学姐学长的机房做的,当时很喜欢剪一个枝交一次,看看每个剪枝的效率,现在看来。。。我的AC率全毁在这个习惯上了,没有任何优化的搜索就得了20分。想了一下加了一个控制循环的剪枝(至少要给后面的每一层留下一个值可取),感觉没什么用,结果得了60。
最后讲一下100分的剪枝:如果剩下的所有层都按照最大的可行体积去做也不够目标体积,剪掉;如果剩下的所有层都按照最小的可行表面积来做也比目前的最优解劣,剪掉;这两个剪枝理论上很强,需要一些预处理,也可以牺牲一点强度写的简单一点:
if((m-w+1)*R*R*H+v<n) return; if((m-w+1)*2+sum>ans) return;
实现上还有一些小细节:第一层的半径:如果高度最小,半径最大,高度最小是$1$,所以半径最大是$\sqrt{n}$,最小显然是$m$;
高度同理;
搜索顺序:半径要从大到小循环,高度从小到大循环。原因引用一句AH学长的话:“高度的变化是线性的,底面积变化是平方的,所以说表面积最小的高度会偏高一些,底面积会偏小一些,这样一个从大到小枚举,一个从小到大枚举就会有更高的效率。”

# include <cstdio> # include <iostream> # include <cmath> using namespace std; int ans=100000000,n,m,sn; bool f=false; void search(int v,int sum,int w,int R,int H) { if(w==m+1) { if(v==n&&sum<ans) ans=sum,f=true; return ; } if(sum>ans) return ; if(v>n) return ; if((m-w+1)*R*R*H+v<n) return; if((m-w+1)*2+sum>ans) return ; int cont1=m-w+1; for (register int r=R-1;r>=cont1;r--) { for (register int h=cont1;h<=H-1;h++) search(v+r*r*h,sum+2*r*h,w+1,r,h); } } int main() { scanf("%d%d",&n,&m); sn=sqrt(n); for (register int r=sn;r>=m;r--) for (register int h=m;h<=n;h++) search(r*r*h,r*r+2*r*h,2,r,h); if(f) printf("%d",ans); else printf("0"); return 0; }
2018.5.30更新:
可以用一些很不错的预处理使剪枝更加有效,加上后快了很多。

# include <cstdio> # include <iostream> # include <cmath> # define re register int using namespace std; int ans=100000000,n,m,sn; int V[20],S[20]; bool f=false; void dfs(int v,int s,int w,int R,int H) { if(!w) { if(v==n) ans=min(ans,s),f=true; return ; } if(s+S[w]>ans) return; if(v+V[w]>n) return; if(s+((n-v)/(R-1)<<1)>ans) return; for (re r=R-1;r>=w;r--) { int minn=min(H-1,(n-V[w-1]-v)/(r*r)); if(w==m) s=r*r; for (re h=minn;h>=w;h--) dfs(v+r*r*h,s+2*r*h,w-1,r,h); } } int main() { scanf("%d%d",&n,&m); sn=sqrt(n); for(re i=1;i<=m;i++) { V[i]=V[i-1]+i*i*i; S[i]=S[i-1]+2*i*i; } dfs(0,0,m,sn,n); if(f) printf("%d",ans); else printf("0"); return 0; }
八数码难题(双向bfs):https://www.luogu.org/problemnew/show/P1379

// luogu-judger-enable-o2 # include <iostream> # include <set> # include <queue> # include <cstdio> # define R register int using namespace std; const int dx[]={-1,0,0,1}; const int dy[]={0,1,-1,0}; int x,dream=123804765; int ans=-1; int q1[10000000]={0}; int b1[10000000]={0}; int q2[10000000]={0}; int b2[10000000]={0}; set<int> s1; set<int> s2; int pul(int n[3][3]) { return n[0][0]*100000000+n[0][1]*10000000+n[0][2]*1000000+n[1][0]*100000+n[1][1]*10000+n[1][2]*1000+n[2][0]*100+n[2][1]*10+n[2][2]; } void un(int now,int n[3][3],int &il,int &jl) { for (R i=2;i>=0;i--) for (R j=2;j>=0;j--) { if(now%10==0) il=i,jl=j; n[i][j]=now%10; now=now/10; } } int A() { int h1=0,h2=0,t1=1,t2=1; int il=0,jl=0,n[3][3],now; while (1) { int dep=b1[h1]; while(dep==b1[h1]) { now=q1[++h1]; if(s2.find(now)!=s2.end()) { for (int i=1;;i++) if(q2[i]==now) return b1[h1]+b2[i]; } un(now,n,il,jl); for (R i=0;i<4;i++) { int xx=il+dx[i]; int yy=jl+dy[i]; if(xx>=0&&xx<=2&&yy>=0&&yy<=2) { int nn[3][3]; for (R ii=0;ii<3;ii++) for (R jj=0;jj<3;jj++) nn[ii][jj]=n[ii][jj]; swap(nn[il][jl],nn[xx][yy]); now=pul(nn); if(s1.find(now)!=s1.end()) { continue; } else { s1.insert(now); q1[++t1]=now; b1[t1]=b1[h1]+1; } } } } dep=b2[h2]; while (dep==b2[h2]) { now=q2[++h2]; if(s1.find(now)!=s1.end()) { for (int i=1;;i++) if(q1[i]==now) return b2[h1]+b1[i]; } un(now,n,il,jl); for (R i=0;i<4;i++) { int xx=il+dx[i]; int yy=jl+dy[i]; if(xx>=0&&xx<=2&&yy>=0&&yy<=2) { int nn[3][3]; for (R ii=0;ii<3;ii++) for (R jj=0;jj<3;jj++) nn[ii][jj]=n[ii][jj]; swap(nn[il][jl],nn[xx][yy]); now=pul(nn); if(s2.find(now)!=s2.end()) { continue; } else { s2.insert(now); q2[++t2]=now; b2[t2]=b2[h2]+1; } } } } } } int main() { scanf("%d",&x); q1[1]=x; b1[1]=0; q2[1]=dream; b2[1]=0; s1.insert(x); s2.insert(dream); ans=A(); printf("%d",ans); return 0; }
以前以为双向bfs可以使时间复杂度减小一半,写完才发现并非如此。
根据原理的话复杂度大概是开方?
事实上也没什么技术含量,如果用记录$color$的做法会比较麻烦,但是开两个$set$就很好写了...把之前的代码进行了优化,展开和压缩都封装成函数,比较简洁。具体思路就是$1$方向将步数相同的状态进行扩展,扔进$set1$里面,如果$set2$中出现过这个状态就加起来作为答案,反之亦然。如果在另一个$set$里出现过这个状态怎么找具体步数?(暴力循环!)恭喜你答对了,这样看起来好像复杂度很高,但是真的高吗...仔细想一想,这样做的复杂度是目前扩展出的结点数总数,但是是加进总复杂度的(只有在$set$里找到了目标状态才会启用这一段程序,找到后会直接$return$,也就是说在整个程序中这段循环最多执行一次)...所以说不影响啊。分析复杂度的时候,不要看到某一个程序段嵌在搜索里就把这一段的复杂度和搜索的复杂度乘起来,具体情况具体分析。
小木棍[数据加强版]:https://www.luogu.org/problemnew/show/P1120
题意概述:有一些等长的小木棍,将它们随意地切断,又想要复原...现在,给出切断后每段的长度,求出原来木棍长度的最小可能值。
首先写一个大暴力,得了33分,是判断每根木棍原先隶属于哪一根做的。这样做的效率低在哪里呢?我猜是因为每一根原木棍并没有顺序,而这样做就会导致重复的搜索。想到这个以后就会发现,确定了原长度后,原根数自然也就可以算出来了,所以从第一根开始搜索,判断是哪些新木棍组成了它,就解决了这个问题(木棍先降序排序)。
在$dfs$中,可以传以下几个参数:组成现在这根木棍还需要多少长度,原来的木棍长度,原来的木棍根数,(比较绕)对于这根原木棍我们已经判断过了前pos根现木棍,已经完成了多少根木棍。
1.如果已经全部拼好了,就返回true;
2.如果这根拼好了,就去拼下一根;
3.其它时间就要从pos+1往后判断是否可以拼起来,一直到这里还都是简单易懂的,再往后就出现了一些难点。
判断完当前这根后,如果可以实现最终答案就应该已经return回去了;如果没有就说明用这一根拼在这里是不行的;那我们可以发现,拼木棍和木棍的编号并没有什么关系,关键是长度,既然这一根拼不成,那和它一样长的其他木棍自然也不能接在这里。用一个while循环把i直接跳到下一个长度。如果拼出当前这根原木棍所需长度正好等于i号木棍的长度,拼上后却没有成功,说明只能用一些更短的木棍拼出这一部分;可是,这样等于说用一些更灵活的木棍来完成不灵活木棍就可以完成的任务,既然这里即使用了不灵活的木棍也拼不出最终答案,那么浪费一些灵活的木棍不就更拼不出来了吗?return掉。如果当前这根原木棍还没开始拼,拼上i号木棍后也无法成功,那等于说i号木棍放在其他地方都更不可能了,于是,return掉。
这么多的剪枝一路剪过来终于A了。

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <algorithm> 5 # include <string> 6 # define R register int 7 8 using namespace std; 9 10 int Max=0,Min,h,x,n,ans=0,ac,S=0,M=0,Sum=0; 11 int a[70]={0}; 12 bool vis[70]={false}; 13 int ii; 14 15 bool dfs(int now,int pos,int d,int T){ 16 17 if (d==T) return 1; 18 if ((!now)&&dfs(ii,1,d+1,T)) return 1; 19 20 for(R i=pos;i<=n;++i) 21 if((!vis[i])&&a[i]<=now){ 22 vis[i]=1; 23 if(dfs(now-a[i],i+1,d,T)) return 1; 24 vis[i]=0; 25 if(now==a[i]||now==ii) return 0; 26 while(a[i+1]==a[i]) i++; 27 } 28 return 0; 29 } 30 31 bool cmp(int a,int b) 32 { 33 return a>b; 34 } 35 36 int main() 37 { 38 scanf("%d",&n); 39 memset(a,0,sizeof(a)); 40 memset(vis,false,sizeof(vis)); 41 Max=0; 42 Sum=0; 43 for (R i=1;i<=n;i++) 44 { 45 scanf("%d",&x); 46 if(x<=50) 47 { 48 a[++h]=x; 49 Sum+=x; 50 } 51 } 52 sort(a+1,a+1+h,cmp); 53 ac=Sum; 54 for (ii=a[1];ii<=(Sum/2)+1;ii++) 55 { 56 if(Sum%ii) continue; 57 if (dfs(ii,1,0,Sum/ii)) 58 { 59 ac=ii; 60 break; 61 } 62 } 63 printf("%d",ac); 64 return 0; 65 }
引水入城:https://www.luogu.org/problemnew/show/P1514
题意概述:感觉并不是很好概述的样子,差不多是说从河岸上建一些水站,可以往低处流水,如果想让沙漠全部被水覆盖,求最少要建几个水站。
这道题是个搜索题,这一点还是比较显然的。之前写的是搜索每一个河岸上的点可以覆盖哪些沙漠点,然后再搜索修哪些水站,只得了40分。
后来发现一个奇妙的性质:如果有解,那么每个水站覆盖的点都是一段连续的区间。为什么呢?
让我们画一个图感受一下:
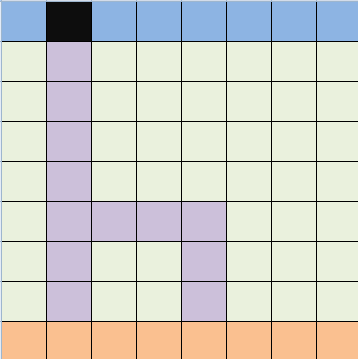
比如说在黑点建了一个水站,水就会顺着紫色线流下来,如果覆盖的区间不连续,就会出现上图所示的情况,紫色的线和沙漠形成了一个闭合的图形。这样一来,两个紫色与沙漠相交的点之间的部分就永远不可能被其他点覆盖了。
用这样的思路,搜出来之后再进行区间的贪心覆盖即可。注意如果无解就不一定满足这个性质了,可以直接调用搜索时的$vis$数组查看有多少点未被覆盖.

1 # include <cstdio> 2 # include <iostream> 3 # include <algorithm> 4 # include <cstring> 5 # define xx x+dx[i] 6 # define yy y+dy[i] 7 # define R register int 8 9 using namespace std; 10 11 const int dx[]={-1,0,0,1}; 12 const int dy[]={0,1,-1,0}; 13 int n,m; 14 int a[505][505]; 15 bool f=false,vis[505][505]; 16 int le[505][505],ri[505][505]; 17 18 inline void dfs(int x,int y) 19 { 20 vis[x][y]=true; 21 for (int i=0;i<4;i++) 22 { 23 if(xx<1||xx>n||yy<1||yy>m) continue; 24 if(a[x][y]<=a[xx][yy]) continue; 25 if(!vis[xx][yy]) 26 dfs(xx,yy); 27 le[x][y]=min(le[x][y],le[xx][yy]); 28 ri[x][y]=max(ri[x][y],ri[xx][yy]); 29 } 30 } 31 32 bool noans() 33 { 34 bool f=false; 35 int ans=0; 36 for (R i=1;i<=m;++i) 37 if(!vis[n][i]) 38 { 39 f=true; 40 ans++; 41 } 42 if(!f) return false; 43 else 44 { 45 printf("0\n%d",ans); 46 return true; 47 } 48 } 49 50 int cov() 51 { 52 int mr,L=1,ans=0; 53 while (L<=m) 54 { 55 mr=0; 56 for (R i=1;i<=m;++i) 57 if(le[1][i]<=L) 58 mr=max(mr,ri[1][i]); 59 ans++; 60 L=mr+1; 61 } 62 return ans; 63 } 64 65 int main() 66 { 67 scanf("%d%d",&n,&m); 68 memset(le,127,sizeof(le)); 69 for (R i=1;i<=m;++i) 70 le[n][i]=ri[n][i]=i; 71 for (R i=1;i<=n;++i) 72 for (R j=1;j<=m;++j) 73 scanf("%d",&a[i][j]); 74 for (R i=1;i<=m;++i) 75 if(!vis[1][i]) dfs(1,i); 76 if(noans()) 77 return 0; 78 printf("1\n%d",cov()); 79 return 0; 80 }
骑士精神:https://www.luogu.org/problemnew/show/P2324
对于这类搜索题真是不知道说什么好了,八数码3*3,四子连棋4*4,这题又来一个5*5的。。。
这题用双向广搜&&估价肯定是可以的,不过这类题大多也都可以用迭代加深搜索来做。其实并不难,但是一开始犯了好多错误(判越界判错,估价估错...)

1 // luogu-judger-enable-o2 2 # include <cstdio> 3 # include <iostream> 4 # define xx (x+dx[i]) 5 # define yy (y+dy[i]) 6 # define R register int 7 8 using namespace std; 9 10 const int dx[]={-1,-1,1,1,-2,-2,2,2}; 11 const int dy[]={2,-2,2,-2,1,-1,1,-1}; 12 bool f=false; 13 char c; 14 int T,no,num,x,y; 15 int goal[6][6],t[6][6]; 16 17 int d() 18 { 19 int ans=0; 20 for (R i=1;i<=5;++i) 21 for (R j=1;j<=5;++j) 22 if(t[i][j]!=2&&t[i][j]!=goal[i][j]) ans++; 23 return ans; 24 } 25 26 bool check(int n,int x,int y) 27 { 28 int tot=d(); 29 if(n+tot>num) return false; 30 if(tot==0) return true; 31 bool s=false; 32 for (R i=0;i<8;++i) 33 { 34 if(xx<1||xx>5||yy<1||yy>5) continue; 35 swap(t[x][y],t[xx][yy]); 36 s|=check(n+1,xx,yy); 37 swap(t[x][y],t[xx][yy]); 38 } 39 return s; 40 } 41 42 int main() 43 { 44 scanf("%d",&T); 45 goal[1][1]=goal[1][2]=goal[1][3]=goal[1][4]=goal[1][5]=1; 46 goal[2][2]=goal[2][3]=goal[2][4]=goal[2][5]=1; 47 goal[3][4]=goal[3][5]=goal[4][5]=1; 48 goal[3][3]=2; 49 while (T--) 50 { 51 f=false; 52 for (R i=1;i<=5;++i) 53 for (R j=1;j<=5;++j) 54 { 55 c=getchar(); 56 while (c!='0'&&c!='1'&&c!='*') c=getchar(); 57 if(c=='1') t[i][j]=1; 58 else if(c=='*') 59 { 60 t[i][j]=2; 61 x=i; 62 y=j; 63 } 64 else t[i][j]=0; 65 } 66 for (num=0;num<=15;++num) 67 if(check(0,x,y)) 68 { 69 f=true; 70 printf("%d\n",num); 71 break; 72 } 73 if(!f) printf("-1\n"); 74 } 75 return 0; 76 }
斗地主:https://www.luogu.org/problemnew/show/P2668
题意概述:单人斗地主。
神题!再让我想一年也不一定能想到正解的题。思索了好久只发现了一件事情,那就是牌的花色似乎没有什么用处,之后就只会爆搜了,疯狂码代码写了180行,然而只有30分。

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # define R register int 5 6 using namespace std; 7 8 int T,n,ans; 9 int a[16]; 10 int num,col; 11 bool id; 12 13 void dfs (int x,int s,int las,int ans) 14 { 15 if(ans==8) printf("I'm working!\n"); 16 if(s==0&&x==ans) 17 id=true; 18 if(id) return; 19 if(x>=ans) return; 20 while (a[las]==0) las++; 21 for (R i=las;i<=13;++i) 22 { 23 if(a[i]<4) continue; 24 for (R j=las;j<=14;++j) 25 { 26 if(a[j]<2) continue; 27 if(i==j) continue; 28 for (R k=las;k<=14;++k) 29 { 30 if(a[k]<2) continue; 31 if(j==k&&a[j]<4) continue; 32 if(i==k) continue; 33 a[i]-=4; 34 a[j]-=2; 35 a[k]-=2; 36 dfs(x+1,s-8,las,ans); 37 a[i]+=4; 38 a[j]+=2; 39 a[k]+=2; 40 } 41 } 42 } // 四带二(对) 43 for (R i=las;i<=13;++i) 44 { 45 if(a[i]<4) continue; 46 for (R j=las;j<=14;++j) 47 { 48 if(a[j]<1) continue; 49 if(i==j) continue; 50 for (R k=las;k<=14;++k) 51 { 52 if(a[k]<1) continue; 53 if(i==k) continue; 54 if(j==k&&a[j]<2) continue; 55 a[i]-=4; 56 a[j]-=1; 57 a[k]-=1; 58 dfs(x+1,s-6,las,ans); 59 a[i]+=4; 60 a[j]+=1; 61 a[k]+=1; 62 } 63 } 64 }// 四带二(个) 65 for (R i=las;i<=14;++i) 66 { 67 for (R j=a[i];j>=1;--j) 68 { 69 a[i]-=j; 70 dfs(x+1,s-j,las,ans); 71 a[i]+=j; 72 } 73 }//火箭&&炸弹&&单张牌&&对子牌&&三张牌 74 bool f; 75 int cnt; 76 for (R i=las;i<=12;++i) 77 { 78 f=true; 79 cnt=5; 80 while (f&&i+cnt-1<=12) 81 { 82 for (R j=1;j<=cnt;++j) 83 if(a[i+j-1]<1) 84 { 85 f=false; 86 break; 87 } 88 if(f==false) continue; 89 for (R j=1;j<=cnt;++j) 90 a[i+j-1]--; 91 dfs(x+1,s-cnt,las,ans); 92 for (R j=1;j<=cnt;++j) 93 a[i+j-1]++; 94 cnt++; 95 } 96 }//单顺子 97 for (R i=las;i<=12;++i) 98 { 99 f=true; 100 cnt=3; 101 while (f&&i+cnt-1<=12) 102 { 103 for (R j=1;j<=cnt;++j) 104 if(a[i+j-1]<2) 105 { 106 f=false; 107 break; 108 } 109 if(f==false) continue; 110 for (R j=1;j<=cnt;++j) 111 a[i+j-1]-=2; 112 dfs(x+1,s-cnt*2,las,ans); 113 for (R j=1;j<=cnt;++j) 114 a[i+j-1]+=2; 115 cnt++; 116 } 117 }// 二顺子 118 for (R i=las;i<=12;++i) 119 { 120 f=true; 121 cnt=2; 122 while (f&&i+cnt-1<=12) 123 { 124 for (R j=1;j<=cnt;++j) 125 if(a[i+j-1]<3) 126 { 127 f=false; 128 break; 129 } 130 if(f==false) continue; 131 for (R j=1;j<=cnt;++j) 132 a[i+j-1]-=3; 133 dfs(x+1,s-cnt*3,las,ans); 134 for (R j=1;j<=cnt;++j) 135 a[i+j-1]+=3; 136 cnt++; 137 } 138 }//三顺子 139 for (R i=las;i<=13;++i) 140 { 141 if(a[i]<3) continue; 142 for (R j=las;j<=14;++j) 143 { 144 if(i==j) continue; 145 for (R k=1;k<=2;++k) 146 if(a[j]>=k) 147 { 148 a[i]-=3; 149 a[j]-=k; 150 dfs(x+1,s-3-k,las,ans); 151 a[i]+=3; 152 a[j]+=k; 153 } 154 } 155 }//三带一&&三带二 156 } 157 158 int main() 159 { 160 scanf("%d%d",&T,&n); 161 while (T--) 162 { 163 memset(a,0,sizeof(a)); 164 for (int i=1;i<=n;++i) 165 { 166 scanf("%d%d",&num,&col); 167 if(num==0) 168 { 169 a[14]++; 170 continue; 171 } 172 if(num>=3) a[num-2]++; 173 if(num==1) a[12]++; 174 if(num==2) a[13]++; 175 } 176 for (ans=1;ans<=n;++ans) 177 { 178 id=false; 179 dfs(0,n,1,ans); 180 if(id) break; 181 } 182 printf("%d\n",ans); 183 } 184 return 0; 185 }
这时候就不知道该怎么做了,后来想到是不是牌的数码也没什么用啊,又发现顺子的判定需要连号,之后就真的不会做了。看了一个有关搜索的课件,里边提到了这道题,还说要先搜顺子,剩下的预处理。太神奇了!因为顺子需要看牌的数码,所以就先把它搜出来好了。剩下的牌就只需要看有几张,而不用管数字是什么。剩下的难度主要在预处理,设$dp[i][j][k][z]$表示出现过一次的数码有i个,出现过两次的数码有j个,出现过三次的数码有k个,出现过四次的数码有z个的最小出牌次数。非常复杂的一番转移下来就很好做了,关键是怎么转移。
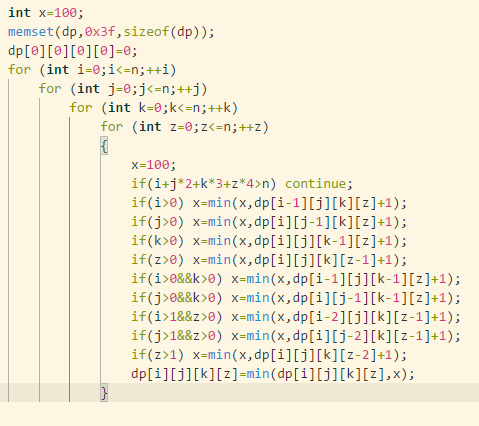
精致!漂亮!其实...也不是很难写呢。

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # define R register int 5 6 using namespace std; 7 8 int T,n,ans; 9 int a[16]; 10 int dp[25][25][25][25]; 11 int num,col,coun[5]; 12 bool id; 13 14 void dfs (int x) 15 { 16 if(x>=ans) return; 17 bool f; 18 int cnt; 19 for (R k=1;k<=3;++k) 20 for (R i=1;i<=12;++i) 21 { 22 f=true; 23 if(k==1) cnt=5; 24 if(k==2) cnt=3; 25 if(k==3) cnt=2; 26 while (f&&i+cnt-1<=12) 27 { 28 for (R j=1;j<=cnt;++j) 29 if(a[i+j-1]<k) 30 { 31 f=false; 32 break; 33 } 34 if(f==false) continue; 35 for (R j=1;j<=cnt;++j) 36 a[i+j-1]-=k; 37 dfs(x+1); 38 for (R j=1;j<=cnt;++j) 39 a[i+j-1]+=k; 40 cnt++; 41 } 42 } 43 coun[1]=coun[2]=coun[3]=coun[4]=0; 44 for (int i=1;i<=14;++i) 45 coun[ a[i] ]++; 46 ans=min(ans,x+dp[ coun[1] ][ coun[2] ][ coun[3] ][ coun[4] ]); 47 } 48 49 void init () 50 { 51 int x=100; 52 memset(dp,0x3f,sizeof(dp)); 53 dp[0][0][0][0]=0; 54 for (int i=0;i<=n;++i) 55 for (int j=0;j<=n;++j) 56 for (int k=0;k<=n;++k) 57 for (int z=0;z<=n;++z) 58 { 59 x=100; 60 if(i+j*2+k*3+z*4>n) continue; 61 if(i>0) x=min(x,dp[i-1][j][k][z]+1); 62 if(j>0) x=min(x,dp[i][j-1][k][z]+1); 63 if(k>0) x=min(x,dp[i][j][k-1][z]+1); 64 if(z>0) x=min(x,dp[i][j][k][z-1]+1); 65 if(i>0&&k>0) x=min(x,dp[i-1][j][k-1][z]+1); 66 if(j>0&&k>0) x=min(x,dp[i][j-1][k-1][z]+1); 67 if(i>1&&z>0) x=min(x,dp[i-2][j][k][z-1]+1); 68 if(j>1&&z>0) x=min(x,dp[i][j-2][k][z-1]+1); 69 if(z>1) x=min(x,dp[i][j][k][z-2]+1); 70 dp[i][j][k][z]=min(dp[i][j][k][z],x); 71 } 72 } 73 74 int main() 75 { 76 scanf("%d%d",&T,&n); 77 init(); 78 while (T--) 79 { 80 memset(a,0,sizeof(a)); 81 ans=n; 82 for (int i=1;i<=n;++i) 83 { 84 scanf("%d%d",&num,&col); 85 if(num==0) 86 { 87 a[14]++; 88 continue; 89 } 90 if(num>=3) a[num-2]++; 91 if(num==1) a[12]++; 92 if(num==2) a[13]++; 93 } 94 dfs(0); 95 printf("%d\n",ans); 96 } 97 return 0; 98 }
写完之后去看了题解区的其他思路,发现这道题对没打过牌的人可以说是极度不友好了,事实上好像只需要模拟手工出牌的方法贪心就可以了,预处理部分变得非常简单。但是,没打过牌的人不知道该怎么贪心啊!!
斗地主增强版:https://www.luogu.org/problemnew/show/P2540
题意概述:相比于上一题增加了一大批构造数据与Hack数据,最大的坑点在于规则不同(这道题不认为两个王是对子。
因为王不再是对子了,只好再开一维用来表示有多少个王。这就比之前复杂的多了。
·三带一要考虑是带王还是带其他;
·四带二单可以带两个其他,一个王+一个其他,两个王;
·四带二双不能带两个王;
但是这样交上去还是不对的,为什么呢?其实是因为之前写的就不够严谨,但是上一题数据太水了就看不出错误来。主要是因为没打过牌不知道还有这种操作。下面让我们来看一些非常神的出牌策略:
·虽然有四个一样的牌,但是把它们拆成3+1;
·把三张牌拆成2+1;
这样的话就又新增了两种转移:
$$dp[i][j][k][z][l]=dp[i+1][j][k+1][z-1][l]$$
$$dp[i][j][k][z][l]=dp[i+1][j+1][k-1][z][l]$$
就又出现了新的问题:等式右边的数还没求过啊!解决方法非常简单粗暴:把这两维循环提到前边去。
下面来欣赏一下新的转移方程:
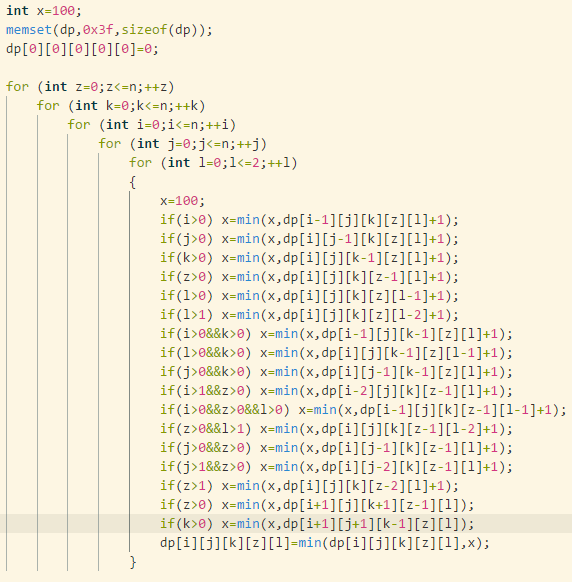
题解区依然有人用神级贪心做了预处理,玩斗地主玩到了一种出神入化的境界。

1 int san_pai() {//贪心打散牌 2 int zs[5],num=0; 3 memset(zs,0,sizeof(zs)); 4 bool wangzha=false; 5 if(pai[1]==2)wangzha=true;//是否有王炸 6 zs[1]+=pai[1]; //王算单牌 7 for(int i=2; i<=14; ++i)zs[pai[i]]++;//统计个数 8 /****** 暴力出奇迹 ******/ 9 while(!zs[3]&&zs[1]==1&&zs[2]==1&&zs[4]>1)zs[4]-=2,zs[1]--,zs[2]--,num+=2;//神特判 10 //把一个炸拆成3张和单牌,再出一组四带二单和三带一 11 while(!zs[2]&&zs[1]==1&&zs[4]==1&&zs[3]>1)zs[3]-=2,zs[1]--,zs[4]--,num+=2;//神特判 12 //把一组三张拆成一对和一单,再出一组四带二单和三带二 13 if(zs[3]+zs[4]>zs[1]+zs[2])//三四张的比单牌和对牌多,拆着打 14 while(zs[4]&&zs[2]&&zs[3])zs[2]--,zs[3]--,zs[1]++,zs[4]--,num++;//拆三张,4带两对余一单 15 if(zs[3]+zs[4]>zs[1]+zs[2])//还多继续拆 16 while(zs[4]&&zs[1]&&zs[3])zs[1]--,zs[3]--,zs[2]++,zs[4]--,num++;//拆三张,4带两单余一对 17 while(zs[4]&&zs[1]>1)zs[4]--,zs[1]-=2,num++;//四带两单 18 while(zs[4]&&zs[2]>1)zs[4]--,zs[2]-=2,num++;//四带两对 19 while(zs[4]&&zs[2] )zs[4]-- ,zs[2]--,num++;//对看成两单再四带 20 if(zs[3]%3==0&&zs[1]+zs[2]<=1) //三张的太多了拆三张 21 while(zs[3]>2)zs[3]-=3,num+=2;//把一组三张拆成单和对,再出三带一和三带二 22 while(zs[3]&&zs[1] )zs[3]-- ,zs[1]--,num++;//三带一 23 while(zs[3]&&zs[2] )zs[3]-- ,zs[2]--,num++;//三带二 24 //还剩三张和炸,组合出 25 while(zs[4]>1&&zs[3])zs[3]--,zs[4]-=2,num+=2;//把一个炸拆成一对和两单,再出三带二和四带两单 26 while(zs[3]>1&&zs[4])zs[4]--,zs[3]-=2,num+=2;//把一个炸拆成两对,再出两组三带一对 27 while(zs[3]>2)zs[3]-=3,num+=2; //同上,把一组三张拆成单和对,再出三带一和三带二 28 while(zs[4]>1)zs[4]-=2,num++; //把一个炸拆成两对,再出一组四带两对 29 if(wangzha&&zs[1]>=2)//有王炸并且没被带跑 30 return num+zs[2]+zs[3]+zs[4]+zs[1]-1;//双王一块出 31 else 32 return num+zs[1]+zs[2]+zs[3]+zs[4];//出剩余的牌,返回答案 33 }

1 // luogu-judger-enable-o2 2 # include <cstdio> 3 # include <iostream> 4 # include <cstring> 5 # define R register int 6 7 using namespace std; 8 9 int T,n,ans; 10 int a[16]; 11 int dp[25][25][25][25][3]; 12 int num,col,coun[5]; 13 bool id; 14 15 void dfs (int x) 16 { 17 if(x>=ans) return; 18 bool f; 19 int cnt; 20 for (R k=1;k<=3;++k) 21 for (R i=1;i<=12;++i) 22 { 23 f=true; 24 if(k==1) cnt=5; 25 if(k==2) cnt=3; 26 if(k==3) cnt=2; 27 while (f&&i+cnt-1<=12) 28 { 29 for (R j=1;j<=cnt;++j) 30 if(a[i+j-1]<k) 31 { 32 f=false; 33 break; 34 } 35 if(f==false) continue; 36 for (R j=1;j<=cnt;++j) 37 a[i+j-1]-=k; 38 dfs(x+1); 39 for (R j=1;j<=cnt;++j) 40 a[i+j-1]+=k; 41 cnt++; 42 } 43 } 44 coun[1]=coun[2]=coun[3]=coun[4]=coun[5]=0; 45 for (int i=1;i<=13;++i) 46 coun[ a[i] ]++; 47 coun[5]=a[14]; 48 ans=min(ans,x+dp[ coun[1] ][ coun[2] ][ coun[3] ][ coun[4] ][ coun[5] ]); 49 } 50 51 void init () 52 { 53 int x=100; 54 memset(dp,0x3f,sizeof(dp)); 55 dp[0][0][0][0][0]=0; 56 57 for (int z=0;z<=n;++z) 58 for (int k=0;k<=n;++k) 59 for (int i=0;i<=n;++i) 60 for (int j=0;j<=n;++j) 61 for (int l=0;l<=2;++l) 62 { 63 x=100; 64 if(i>0) x=min(x,dp[i-1][j][k][z][l]+1); 65 if(j>0) x=min(x,dp[i][j-1][k][z][l]+1); 66 if(k>0) x=min(x,dp[i][j][k-1][z][l]+1); 67 if(z>0) x=min(x,dp[i][j][k][z-1][l]+1); 68 if(l>0) x=min(x,dp[i][j][k][z][l-1]+1); 69 if(l>1) x=min(x,dp[i][j][k][z][l-2]+1); 70 //单权值 71 if(i>0&&k>0) x=min(x,dp[i-1][j][k-1][z][l]+1); 72 if(l>0&&k>0) x=min(x,dp[i][j][k-1][z][l-1]+1); 73 //三带一 74 if(j>0&&k>0) x=min(x,dp[i][j-1][k-1][z][l]+1); 75 //三带二 76 77 if(i>1&&z>0) x=min(x,dp[i-2][j][k][z-1][l]+1); 78 if(i>0&&z>0&&l>0) x=min(x,dp[i-1][j][k][z-1][l-1]+1); 79 if(z>0&&l>1) x=min(x,dp[i][j][k][z-1][l-2]+1); 80 if(j>0&&z>0) x=min(x,dp[i][j-1][k][z-1][l]+1); 81 if(j>1&&z>0) x=min(x,dp[i][j-2][k][z-1][l]+1); 82 if(z>1) x=min(x,dp[i][j][k][z-2][l]+1); 83 //四带二 84 if(z>0) x=min(x,dp[i+1][j][k+1][z-1][l]); 85 if(k>0) x=min(x,dp[i+1][j+1][k-1][z][l]); 86 dp[i][j][k][z][l]=min(dp[i][j][k][z][l],x); 87 } 88 } 89 90 int main() 91 { 92 scanf("%d%d",&T,&n); 93 init(); 94 while (T--) 95 { 96 memset(a,0,sizeof(a)); 97 ans=n; 98 for (int i=1;i<=n;++i) 99 { 100 scanf("%d%d",&num,&col); 101 if(num==0) 102 { 103 a[14]++; 104 continue; 105 } 106 if(num>=3) a[num-2]++; 107 if(num==1) a[12]++; 108 if(num==2) a[13]++; 109 } 110 dfs(0); 111 printf("%d\n",ans); 112 } 113 return 0; 114 }
$Addition$ $Chains$:https://loj.ac/problem/10021
这道题题面本身就非常简洁了.
考虑搜索,循环时从大到小搜比较快(要用较少的数字拼出$n$)但是这样可能一次扩展到底,而且中间无法剪枝,所以可以尝试先对搜索树的深度进行一个估界.如果先每次用$2$的幂拼凑,快速拼出比$n$小的最大的数,然后用二进制拼出来,这样构造的解实际上已经非常优秀了,以它的长度作为剪枝的依据即可.$loj$把一百组数据塞到一起按$1s$算是为什么...果断打表.

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # include <algorithm> 6 # include <cmath> 7 # define R register int 8 # define ll long long 9 10 using namespace std; 11 12 const int maxn=102; 13 int a[maxn],n,T,p,po,minlen,t[maxn*10],ans[maxn]; 14 bool f; 15 16 void write (int x) 17 { 18 if(ans[x]!=n) return ; 19 f=true; 20 minlen=x; 21 for (R i=1;i<=x;++i) 22 a[i]=ans[i]; 23 } 24 25 void dfs (int x,int dep) 26 { 27 if(x==dep+1) write(x-1); 28 else 29 { 30 for (R i=min(ans[x-1]*2,n);i>ans[x-1];--i) 31 for (R j=x-1;j>=0;--j) 32 if(i>=ans[j]&&t[ i-ans[j] ]) 33 { 34 ans[x]=i; 35 t[ i ]++; 36 dfs(x+1,dep); 37 t[ i ]--; 38 } 39 } 40 } 41 42 int main() 43 { 44 scanf("%d",&n); 45 while(n) 46 { 47 T=0,p=1; 48 a[++T]=1; 49 while(a[T]*2<=n) a[T+1]=a[T]*2,T++; 50 t[1]=1; 51 ans[1]=1; 52 f=false; 53 minlen=T; 54 while(!f) 55 { 56 memset(ans,0,sizeof(ans)); 57 ans[1]=1; 58 dfs(2,minlen); 59 if(f) break; 60 minlen++; 61 } 62 for (R i=1;i<=minlen;++i) printf("%d ",a[i]); 63 printf("\n"); 64 scanf("%d",&n); 65 } 66 return 0; 67 }
以前觉得折半搜索就是双向搜索,今天才发现不是...
世界冰球锦标赛:https://www.luogu.org/problemnew/show/P4799
题意概述,给出$n$个数,要求从中选出一些数,且这些数的和不超过$m$,求选数的方案数.$n<=40,m<=10^18$
$meet$ $in$ $the$ $middle$往往有一个显著的特征:搜索的顺序对答案没有影响或是稍微再记录一些信息后就能消除影响.
首先这个 $40$ 的范围就很奇怪了,因为如果是普通的多项式级别算法甚至可以开到 $n^5$ ,但是 $m$ 太大,如果是指数级又跑不过,看起来比较有可能的一种算法是 $N^4logM$ .
于是就引出了这道题的算法:折半搜索,因为$2^20$看起来是个不错的复杂度。
首先搜索前半部分得到一些数,放进一个队列里,然后搜索后一半,放到另一个队列里。两个队列分别排序,这样对于左边的每一个元素对应可以匹配的右边元素是一个区间,而且随着左边元素大小的增加,转移区间的转移是单调的,维护两个指针指向头尾即可.注意...不要每次都把左指针从右指针开始往左扫,而是从上回结束的地方接着扫...左边的区间是$[1,mid]$,右边是$[mid+1,n]$

1 # include <cstdio> 2 # include <iostream> 3 # include <cstring> 4 # include <string> 5 # include <algorithm> 6 # include <cmath> 7 # define R register int 8 # define ll long long 9 10 using namespace std; 11 12 const int maxn=41; 13 int n,l,r; 14 ll m,a[maxn],ans,x; 15 ll lef[1<<21],rig[1<<21]; 16 17 void dfs (int x,int l,int r,int col,ll S) 18 { 19 if(x==r+1) 20 { 21 if(col==1) lef[ ++lef[0] ]=S; 22 else rig[ ++rig[0] ]=S; 23 return ; 24 } 25 dfs(x+1,l,r,col,S+a[x]); 26 dfs(x+1,l,r,col,S); 27 } 28 29 int main() 30 { 31 scanf("%d%lld",&n,&m); 32 for (R i=1;i<=n;++i) 33 scanf("%lld",&a[i]); 34 int mid=n/2; 35 dfs(1,1,mid,1,0); 36 dfs(mid+1,mid+1,n,2,0); 37 sort(lef+1,lef+lef[0]+1); 38 sort(rig+1,rig+rig[0]+1); 39 l=-1; 40 r=rig[0]; 41 for (R i=1;i<=lef[0];++i) 42 { 43 x=lef[i]; 44 while(r&&x+rig[r]>m) r--; 45 if(l==-1) l=r; 46 while(l&&x+rig[l]<=m) l--; 47 ans+=(r-l); 48 } 49 printf("%lld",ans); 50 return 0; 51 }
---shzr



