《形式语言与自动机》复习笔记
数分考完(11:30)到自动机开始考(次日9:00)只有不到22小时,而中间还要睡觉和吃饭,我哭死。
明天考完数分就开始极速复习自动机!先把博客发出来以免明天又鸽了,呜呜
Upd:发博客并不能防止我不鸽,现在是晚上八点半。考完数分后直接失去了全部复习动力!先是玩了好久风行迷踪,然后躺在床上睡不着,又看了好多三体动画的二创……下午发现外卖突然恢复了,狂喜,点了杯奶茶。不能说一点没复习,但也差不多吧……
捏捏说现在申请缓考很可能过不了,想想还是赶紧复习吧,ww
一些概念
复习的时候感觉很多概念都记不清楚,先在这里写下:
$\sum$:字母表,一些符号的非空有限集合。
字符串:字母表中字符构成的一个有限序列,空串用 $\epsilon$ 表示。
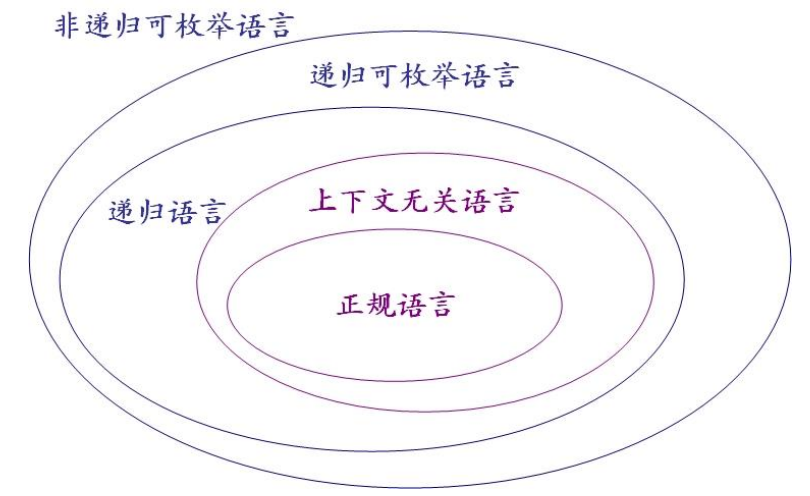
正规语言-正规表达式-有限自动机
上下文无关语言-上下文无关文法-下推自动机
图灵机-
上下文无关文法(CFG):$G=(V,T,P,S)$
V:非终结符的集合;T:终结符(不能再进一步变换了)的集合;P:产生式的集合;S:开始符号;满足V,T的交集为空,开始符号属于非终结符。
上下文无关语言:上下文无关文法产生的语言。L(G)
确定有限状态自动机(DFA):$A=(Q,\sum,\delta,q_0,F)$
Q:有限状态集;sum:有限输入符号集;delta:转移函数;q0:开始状态;F:一个终态集合
非确定有限状态自动机(NFA):形式同DFA,但每个delta的因变量可以是一个集合(转移到这几个状态中的某个)。
DFA和NFA产生的都是正规语言。
下推自动机 PDA:$P=(Q,\sum,\Tau,\delta,q_0,Z_0,F)$
参数分别是,状态集合,输入符号集,栈符号集,转移函数,开始状态,开始堆栈符号,终态集合
Chapter2 上下文无关文法
从开始符号推到所需字符串叫推导;从所需字符串恢复到开始符号叫归约。
推导过程的每一步总是替换出现在最左边的非终结符,叫最左推导;最右推导同理。
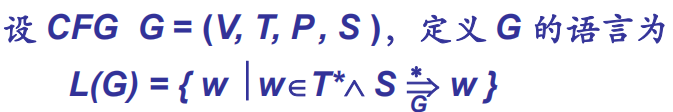
证明思路:归纳推导的步数。
一个CFG是否为二义是不可判定的。消除二义性的一些可能方法:优先级,最近匹配
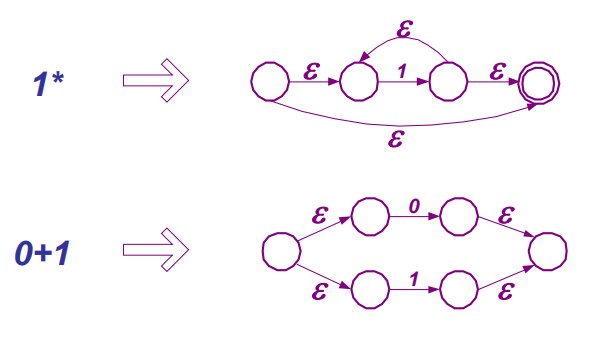
Chapter3 正规表达式
算符优先级:*>·(连接)>+
定义:L?=L+空串
代数定律:将正规表达式中的每个变量换成单个符号再证明。
Chapter4 有限状态自动机
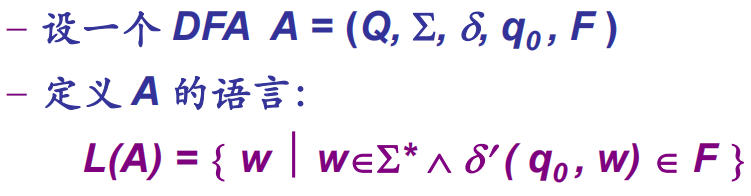

DFA和NFA是等价的。
DFA转NFA:DFA本身就可以看成是一种NFA吧。
NFA转DFA:子集构造法。
带有空转移边的NFA和DFA也是等价的。
自动机最小化:填表法,看看哪些状态是不可区分的,捏成同一个。
Chapter5 有限状态自动机
表达式 转 带空转移的NFA:
DFA转表达式:路径迭代法;状态消去法;
Chapter6 正规语言的性质
Pumping定理:可用于证明某些语言不是正规语言。

判定性质:
是否为空:直接看(表达式)或从初态出发看是否可达终态(自动机)。
是否包含特定的w:放上自动机走一走(自动机)转成自动机然后参照上一条(表达式)。
判定两个语言是否相同:把两个自动机重命名到没有重名的状态。然后按照最小化的方式填表,如果最后填出来两个自动机初态不可区分,那就是相同的语言了。
正规语言的封闭运算:
并,补,交,差,反向,(星)闭包,连接,同态,反同态
证明封闭性:若L为正规语言,则存在正规表达式,有L(R)=L,然后由正规表达式得出答案;根据已有的自动机构造新自动机等。
不是正规语言也可以用封闭运算来证明。
Chapter7 下推自动机
转移函数这样写,意思是当前在q0状态,输入字符为0,栈顶为Z0时应该转移成什么样子。
用ID表示当前格局(q,w,y),表示(当前状态,剩余的输入串,栈的内容)
终态接受的定义方法:某些状态是接受态。
空栈接受的定义方法:栈为空时是接受态。
两种定义方法可以互相转换:(终态到空栈)加上终态时可以随意消除栈的转移边;(空栈到终态)先在栈里塞一个标志,等栈里只剩标志的时候就可以跳转到终态。
Chapter8 上下文无关文法-下推自动机
上下文无关文法->自动机:甚至可以只有一个状态,相当于模拟最左推导(?
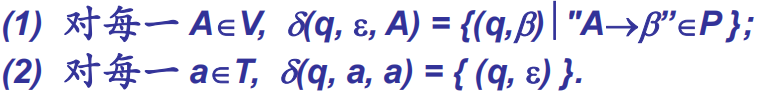
自动机->上下文无关文法:我的评价是十分奇怪……
先休息一下等会写这块
Chapter9 确定下推自动机
每个delta只转移到一个状态,且如果一个状态能用实际的字符转移,就不能同时存在空转移(那就不知道该怎么转移啦!)
这样的下推自动机叫确定下推自动机(DPDA)。
正规语言都可以用确定下推自动机表示。因为可以用DFA表示,所以根本不需要栈……
DPDA的计算能力比有限自动机强。(毕竟多了一些功能)
前缀性质:(语言L的性质)不存在x是y的前缀,而且xy都属于L的情况。则称L具有前缀性质。
![]()
一个语言L满足前缀性质 当且仅当 L是某个空栈接受的DPDA的语言。
某些上下文无关语言不是任何DPDA的语言。如果一个上下文无关语言能被表示成某个DPDA的语言,则称他为一个确定的上下文无关语言。
一个语言L是某个空栈接受的DPDA的语言 则 L存在一个无二义文法。(其实只要L是某个DPDA的语言,就都成立)
如果L固有二义,则不是任何DPDA的语言。但如果不是固有二义,也可能不是任何DPDA的语言。

Chapter10 CFG的简化以及Chomsky范式
简化:1)消去无用符号;2)消去空产生式;3)消去Unit产生式;
有用符号:开始符号推到某个结束状态的过程中用到的符号;无用符号:用不到的符号;
生成符号:称X是生成符号,当且仅当X可以推导到一个w;(从终结符号倒推)
可达符号:X是可达符号,满足S可以推到aXb;(从S正着推)
消去所有的非生成符号和所有的非可达符号,剩下的就都是有用符号了,而且等价。
1)步骤:计算生成符号,计算可达符号,消去非生成和非可达。
晕了,等会写
Chapter11 上下文无关语言的性质
证明不是上下文无关:

判定上下文无关文法是否为空:计算生成符号,然后判断开始符号是不是生成符号。
是否包含指定字符串:变为Chomsky范式,然后用CYK算法。

关于上下文无关几个不可判定的问题:给定的文法是否无二义?是否固有二义?两个语言是否相交?两个语言是否相等?语言是否等于全集?
封闭运算:替换,并,反向,闭包,连接,同态,反同态,与正规语言的交。
此处的替换真的超级自由,甚至可以这样:
![]()
注意,对于上下文无关语言(CFL),交,补,差就不一定还是CFL了!
Chapter12 图灵机


可以被图灵机接受的语言:递归可枚举语言
停机:不存在下一个移动
递归语言:对于属于L(M)的语言,M可以接受;对于不属于L(M)的语言,M也可以停机;(递归语言对应的问题都是可判定的)
还有好多花里花哨的图灵机变种,但似乎……差别都不大。
Chapter13 计算理论
对角语言不是递归可枚举语言。
如果L是递归语言,那么L的补也是递归语言。但递归可枚举语言的补不一定还是递归可枚举了。
通用语言:L_u,具体是啥我不知道,也不想知道了。他是递归可枚举的,但不是递归的。而他的补连递归可枚举都不是了。
语言对应的问题:任给一个串w,w属于L是否成立?
递归语言对应的问题是可判定的,否则不可判定。如果是递归可枚举,则是“部分可判定的”
图灵机停机是不可判定的!
Rice定理:关于递归可枚举语言的任何非平凡性质都是不可判定的。
Post对应问题:两组二进制串,如何拼拼能正好序号一样长得也一样。(这个是不可判定的)
一个给定的CFG是否歧义也无法判定的。
图灵机+复杂度多项式=P问题;非确定图灵机+复杂度多项式=NP问题
NP-完全:p是NP,且任意NP可以多项式规约到p,则p是NP完全。
NP-难:不知道p是不是NP,但任意NP可以多项式规约到p,则p是NP难。
可满足性问题(SAT)是NP-完全。
终于整理完了(?可我还是啥也不会,令人感叹
一些三体二创
真的很好,所以放在这里分享给大家。
大法师罗辑:https://www.bilibili.com/video/BV17e4y1L7kJ
三体x原神:https://www.bilibili.com/video/BV1kv4y1X7w6
后记

考试前真的完全麻了,因为12.31晚上计系概,1.2早大物,1.3早数分,1.4早自动机。想到数分肯定要复习很久,我就把大物缓考了。结果考完数分后一点不想复习,从晚上七点多才开始认真复习,结果发现第12、13章我就跟没见过一样……
总之,精神状态参照上述两行聊天记录,凌晨快两点的时候,我还拿着手机躺在床上看ppt(
第二天早上开始考试,一发卷子更麻了,发现题巨多,而且刚开始就有两个选择不确定。梦游般做完了考试,交上卷子后意识到至少有15分的构造题约等于没写(或者说写了,但我100%确定是错的),但因为这是期末的最后一门考试,考完就开始快乐了~
自动机出成绩很晚,春季学期都开学快两周了才出卷面成绩,我一点进去发现得了80,感到非常震惊,看来只要写了的基本都对了?四处打听了一下发现这个分数还可以,而且我期中其实相当高,所以就放心了。晚上逛树洞,发现有人说自动机不调分,算了一下发现不到90(期末占比70%,纯毒瘤),再次麻了。
好在最后竟然是A-,赢!(而自认为复习得很好+考得很好的计系概反而是B+,输)


