计算几何学习笔记

　　我竟然开始学习计算几何了！太太太太太太不容易啦！

　　latex的向量表示真的令人窒息：$\vec{a},\vec{b}$；箭头高度竟然不能统一！不仅加箭头很不对劲，加粗还常常bug，所以下面只要出现小写字母，代表的都是向量，大写字母代表点；

　　

　　计算几何做起题来真真真真的太难了（指卡精度），所以做累了题目，可以来看看这篇文章摘要的小圆球，很可爱鸭！

点积

　　$a\cdot b=|a||b|\cos\left \langle a,b \right \rangle$，类似于物理中的做功；

　　坐标表示下，则有： $a\cdot b=x_1x_2+y_1y_2$ ；

　　应用：两向量垂直，点积为0，反之亦然；

叉积

　　$a\times b=|a||b|\sin\left \langle a,b \right \rangle$，求出的是 $a,b$ 张出的平行四边形的有向面积，当 $b$ 在 $a$ 的逆时针方向时为正，否则为负；

　　坐标表示下，则有： $a\times b=x_1y_2-x_2y_1$ ；　　

　　应用：两直线平行，叉积为0，反之亦然；还可以用来算面积；

向量旋转

　　将向量 $a=(x,y)$ 逆时针旋转 $\theta$ 度后：$(x\cos \theta-y\sin\theta,x\sin \theta+y\cos\theta)$ ；

　　为什么？

　　设 $a$ 与 $x$ 轴夹角为 $\alpha$，则有 $x=|a|\cos\alpha,y=|a|\sin \alpha$；

　　旋转后：$x'=|a|\cos(\alpha+\theta),y'=|a|sin(\alpha+\theta)$；

　　$x'=|a|cos\alpha \cos\theta-|a|\sin\alpha \sin \theta,y'=|a|\sin\alpha\cos\theta+|a|\cos\alpha\sin\theta$

　　$x'=x\cos\theta-y\sin\theta,y'=x\sin\theta+y\cos\theta$；

求直线交点

　　这里没有图！因为插入图片真真真真的不好看，所以我会写的很仔细，自己画图看吧qwq；

　　设直线 $AB$ 与直线 $CD$ 交于点 $O$；作 $CH_1\perp AB$，垂足为 $H_1$，作 $DH_2\perp AB$，垂足为 $H_2$；

　　$S_{ABC}:S_{ABD}=CH_1:DH_2$；这里用叉积可以求出两三角形面积；

　　可以发现：$\Delta OCH_1\sim\Delta ODH_2$，所以 $S_{ABC}:S_{ABD}=CH_1:DH_2=CO:DO$

　　这样就可以求出 $O$ 的坐标啦；

　　很好玩的一点是，即使线段AB与线段CD根本没有交点，这个算法也可以正确求出两条直线的交点；不过这里有一点需要注意：三角形面积必须是有向面积才可以；证明比较简单，画画图就明白了；

　　嗯，上述是美好的理论，实际上写起来还是有一定困难的...因为一旦涉及到除法，就要考虑是否会出现/0的问题...有没有什么是一定不为0，可以安安全全做分母的呢？其实还真的有！那就是 $\overrightarrow {AB}\times \overrightarrow {CD}$ ，只要有交点，叉积的值一定不为0。所以最好是能找到一种方法，整个式子里唯一的分母就是这个叉积；

　　连接 $AC$，延长 $OD$ 使得 $|OD'|=|CD|$，延长 $OB$ 使得 $|OB'|=|AB|$ ；求 $s1= \overrightarrow {AC}\times \overrightarrow {AB},s2= \overrightarrow {AB}\times \overrightarrow {CD}$；则 $k=\frac{s1}{s2}=\frac{ \overrightarrow {CO}}{ \overrightarrow {CD}}$ ；则 $ \overrightarrow {O}= \overrightarrow {C}+ \overrightarrow {CO}= \overrightarrow {C}+k \overrightarrow {CD}$；

求多边形面积

　　已知一个多边形的顶点按照逆时针顺序排列，则其面积为：

　　$P_1\times P_n+\sum_{i=1}^{n-1}P_i\times P_{i+1}$

　　证明如下（抄的课件）：

圆的交点

　　

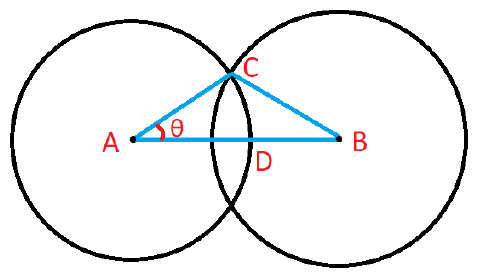
　　$AC=r_1,AB=d(A,B),CB=r_2$；

　　既然三角形的三边都知道了，我们就可以利用余弦定理求出 $\theta$ ：

　　$\theta=acos\left(\frac{|AC|^2+|AB|^2-|BC|^2}{2|AC|\times|AB|}\right)$

　　然后把 $\overrightarrow {AD}$ 逆时针旋转 $\theta$ 度就可以得到 $\overrightarrow {AC}$ 了；

圆的公切线

　　

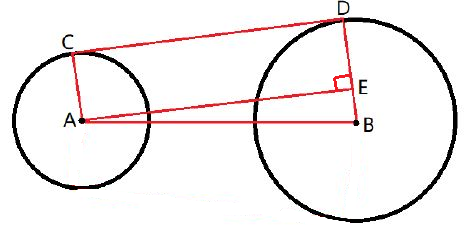
　　$AB=d(A,B),BE=r_2-r_1,AE=\sqrt{|AB|^2-|BE|^2}$；

　　使用反三角函数求出 $EAB$ 的角度，旋转并缩放 $AB$ ，这样就可以得到 $AC,BD$ 啦；

凸包

　　Graham感觉比较一般，还要求极角序，感觉挺容易炸精度的...

　　我个人感觉Andrew稍微好一点吧，所以就讲这个：

　　首先所有点按照横坐标排序（升序），横坐标相同的按纵坐标排序（升序）；

　　顺序枚举每个点，看看能消掉多少个点（形如_/的拐点就应该删掉），然后将它加入；这个过程中，我们还需要一个栈来维护当前生成的凸包；（注意，如果两个点纵坐标相同，只保留第一个在栈中）；

　　这样以后，就可以求出下凸包，倒着来一遍，就求出了上凸包；

　　这个方法其实是很妙的，首先它不会出现三点共线，横坐标最小的点有很多也没关系，反正只会是纵坐标最大的进了上凸包，纵坐标最小的进了下凸包；不过，如果横坐标最小的点唯一，它就会同时出现在上下凸包中，这里要注意一下下；

旋转卡壳

　　求凸包直径的好算法，同时也可以解决一些别的问题；

　　以前看了n遍也不懂，今天看了看结果秒懂，果然以前太傻了吗？

　　首先凸包的直径一定是凸包上两点的距离；我们可以用一对平行直线卡住这个凸包，可以发现，凸包的直径一定可以被卡出来；但是卡点有点麻烦，由于凸包形状可以很诡异，如果我们顺次枚举凸包上每个点去找它的最远点，其实没有什么很好的性质；

　　卡凸包还有一种方法，就是钦定一条直线和某一条边重合，另一条直线卡到一个点上。显然，这样可以枚举到所有的对踵点对；而随着直线斜率的连续变化，另一条直线的卡点的可行区间在凸包上是单调移动的，这样我们就可以 求出所有对踵点对了；在移动卡点的过程中，如果发现移动后点到直线的距离变小了，那么它们之间一定无法构造平行卡壳（证明可以考虑凸包上边的斜率），所以这一步就不能再动了；(凸包上点到给定边的距离单峰，因为凸包类似一个圆形)

　　对于找到的"离这条边最远的点"，我们计算它到卡边两端点的距离，最后就可以得到凸包直径了；

　　注意：旋转卡壳并不能求出所有点的最远点是谁；

 

半平面交

　　半平面指的是二维平面上一条直线一侧的所有空间，通常使用点对 $(A,B)$ 表示在 $\overrightarrow {AB}$ 左侧的半平面；半平面交的解析式为 $Ax+By+c\geq 0$；

　　多个半平面的交要么是空集，要么是非空的凸集；

　　暴力（我以前连暴力也不会呜呜呜）：维护一个多边形表示半平面的交集，每次加入一个新的半平面去切割多边形，得到新的顶点；复杂度 $\rm O(n^2)$；具体怎么实现呢？（以下为我自己想的，未必对）：首先自然是需要一个无限大的矩形框，每次加入半平面时，首先将已有的边分为三种：“完全在半平面内的”，“完全在半平面外的”，“一般在半平面内，一般在半平面外的”；第一种的端点自然要保留，第二种的端点直接删掉，对于第三种，删掉那个平面外的，并新加入一个线段与半平面边界的交点；（感觉没啥问题吧）

　　那么现在我们来学习一个更好的算法吧！

　　先来介绍一下极角，极角就是向量与x轴正方向的夹角，$\theta\in(-\pi,\pi]$；求法很简单，直接利用C++函数 $atan2(y,x)$ ，这个函数的作用是返回 $\arctan\frac{y}{x}$；

　　求半平面交以前，先把所有半平面按照极角排序（升序）；

　　思考暴力的过程，可以发现半平面交最后一定是一个凸多边形，且每条边都是原来的某个半平面的一部分，每个顶点都是两个半平面的交点；这是我以前一直没想明白的，所以感觉半平面交很玄学，想明白这些边都是以前就存在的就会好做很多了...吧；

　　按照极角序，依次把半平面插入，插入过程中，可能会有部分半平面被删掉，像这样：

　　

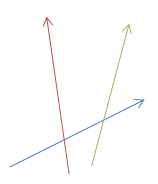
　　插入红色后，绿色就没用了；我们把它删掉；当然，也有可能需要删掉很多个；

　　一个有趣的现象是还可能删掉最早加入的几个，这个比较显然...所以我们需要用双端队列来维护半平面交；

　　那么什么时候会删掉半平面呢？如果两个早已加入的半平面的交点在新半平面的右边，那它们中就得删掉一个，具体删哪个得看现在是在处理队首还是队尾；

　　全部插入完成后，再看看能不能用队首从队尾弹出去几个；不过，不需要让队尾弹出队首，因为在插入队尾时其实已经考虑过这些问题了...

　　小细节：要先弹队尾再弹队首。为什么？画一个队列里只有两个元素且要弹出的例子就会明白了；

　　一点优化：对于极角相同的线段，只需保留靠左的那个；

　　半平面交的某个应用是求多边形的核：如果一个点集中的点与多边形上任意一点的连线与多边形没有其他交点，那么这个点集被称为多边形的核。方法很简单，就是给多边形上的边定向（定向后成为一个环），每条边取多边形内部的那个半平面求交，交集就是多边形的核；