CSP-S赛前冲刺
Day 1:

得分:55=20+35+0; rk:36;
序列
首先,奇数偶数互不影响,所以可以分开考虑。如果序列的长度为偶数,那么还得分为“首位是奇数”和“首位是偶数”两种情况考虑,这倒不难,把两种答案都算出来最后比较即可。
显然,如果需要重排代价最小,所有数仍按顺序填上就是一组合法解。现在我们来考虑如何使字典序最小;
设 $x_i$ 表示第 $i$ 个数的匹配位置比原位置是往左了/没变/往右了;如果一个数位置没变,那一定不能改变它的位置,对于另外两种情况,只要满足交换后不改变 $x_i$,那么代价也是不变的。考试的时候有点降智,没发现 $x_i$ 不变,其实挺显然的...另一个性质:每个数只会和自己所在的 $x_i$ 相同的那一段里的数进行交换;不过这个注意不到好像也没问题呃...总之我们现在拿出 $x_i$ 相同的一段区间,对这些值进行重排。首先考虑数字匹配右边的位置的情况,为了字典序最小,从前往后考虑每个位置,匹配它以前最小的值即可;然后考虑数字往左匹配的情况,这时情况有一些复杂,因为不能从前往后选最小的了(这样可能导致后面某些点没得选)。于是我们从后往前,尽量选择最大的匹配,把小的留给前面...这样不是反向字典序最大吗?和字典序最小不等价吧...但是呢,你会发现通过反证法还真能证明这个策略是最优的...我猜测这和“每个位置可以匹配的数是一段后缀”不无关系。啊,总之反证能证出来,那就说明它是对的嘛...
灯泡
需要用到一个结论:树的联通块数=点数-边数;对于这道题:区间数=亮灯数-“不仅自己亮着,前一个也亮着”的灯数;一个方便编程的优化:将颜色相同的段缩起来;
亮灯的数量显然很好维护,只要预处理每个颜色的灯有几个,并维护每个颜色现在是否点亮就好了。
现在来想想怎么维护“亮灯对”。暴力?暴力倒是很好写,只要在开灯关灯时顺便维护“亮灯对”就可以了,但是会很慢;仔细观察数据范围:2e5;启示根号算法?来尝试一下根号分治吧!
将出现次数小于等于 $B$ 的视为小点,否则视为大点。对于“小-小”的数对很好处理,开关灯时顺便检查就好;“大-大”的数对也很容易,预处理每对大点之间有多少条连边,每次暴力查看所有大点也花不了多少时间;稍微困难的是“小-大”数对,考虑在暴力小点时,在大点处打标记,记录每个大点有多少相邻的亮着的小点,这样在操作大点时,便可以方便地维护“小-大”数对的数量了;复杂度 $O(n\sqrt{n})$.
比赛
这题坑我啊!每个subtask里都有 $p=0,p=1$ 的测试点,而我的程序无法处理这种情况,当场去世.jpg
首先可以发现,不可能出现一种 “可以从中选出多个大小为 $x$ 的合法集合”的局面;所以,对于一个确定的 $x$,一个局面要不无法选出 $x$ 个人,要不可以选出确定的 $x$ 个人;这样我们就不用担心两个集合存在于一种局面下的问题了(如果有这种情况就没法算了,如果一个局面可以找到多个合法集合,这个局面就可能被多次计数);
设 $f_{i,k}$ 表示考虑了 $i$ 个人,可以给 $k$ 个人颁奖的概率,$q=1-p$ ;这里有一个小技巧:只考虑新加进来的人和以前的人产生的贡献,这样就一直是在乘概率;我以前的做法是每次新加进一个数时,除掉以前的人和他产生的不合法概率,这样如果概率是0就挂了;考虑新加进来的人,发现他是什么编号都有可能,因为我们只是说" $i$ 个人",又没说是"前 $i$ 个人"。既然他的编号不固定,那就先设为 $i+1$;转移时考虑这个人是否颁奖,可以得到:
$f_{i+1,k}=p^k\times f_{i,k}+q^{i-k+1}\times f_{i,k-1}$
这样就可以 $n^2$ 来做了;另一方面,我们给新加的人换个编号,会不会有奇效呢?为了方便,这回设成最小编号:
$f_{i+1,k}=q^k\times f_{i,k}+p^{i-k+1}\times f_{i,k-1}$
看上去,两个式子联立可以消掉一些量:
$p^k\times f_{i,k}+q^{i-k+1}\times f_{i,k-1}=q^k\times f_{i,k}+p^{i-k+1}\times f_{i,k-1}$
$f_{i,k}\times(p^k-q^k)=f_{i,k-1}\times(p^{i-k+1}-q^{i-k+1})$
$f_{i,k}=f_{i,k-1}\times \frac{p^{i-k+1}-q^{i-k+1}}{p^k-q^k}$
另外,$f_{n,0}=1$,因为不选人总是可以的。这样,就可以 $O(n)$ 地递推出所有的 $f_{n,k}$ 了。
还有一个小问题!如果 $p=q$ ,那么就会变成 $0=0$ ,无法再推下去了。
不过呢,既然 $p=q=\frac{1}{2}$,那么获胜的概率就和编号无关啦,可以直接得到答案:
$f_{n,k}=\binom{n}{k}\frac{1}{2^{k(n-k)}}$
Day 2:

得分:240=100+60+80; rk:9;
石子
$E(t_1)=1+\sum_{i=2}^nP(t_i<t_1)=1+\sum_{i=2}^n\frac{a_i}{a_1+a_i}$
内存
一个显然的做法:枚举x,对于每个x计算答案后取 $\max$;因为要“最大值最小” ,很容易想到二分,二分最大值后,就可以贪心地分段,最后看看段数是否超了就好;这样 $check$ 一次的复杂度为 $O(n)$ ,总复杂度 $O(mn\log S)$;
这样是无法通过的(虽然就差一点点),思考如何优化;一个稍微容易想到的策略是这样的:顺序枚举 $x$ 的同时,维护当前找到的最优解 $ans$,对于一个新的 $x$,首先判断 $ans-1$ 是否可以达成,如果不行,那这个 $x$ 根本不可能更新答案,直接跳过就好了。这样虽然可以稍微加快速度,但是却不能改变复杂度;嗯然后对所有的 $x$ 先来一个 $random\_shuffle$ 就可以通过了...这就是玄学的力量?不不不,其实这个是有复杂度保证的;首先,对于每个 $x$ 能够计算出来的最终答案,将其设为 $ans_x$,因为已经被打乱了,所以可以将 $ans_x$ 看做一个随机序列。$x$ 可以更新答案当且仅当 $ans_x$ 是一个严格前缀最小值。一个长度为 $n$ 的随机序列期望情况下有多少个前缀最小值呢?$\ln n$ 个...证明十分容易:前 $i$ 个数中,最小值恰在最后的概率为 $\frac{1}{i}$,所以前缀最小值的期望个数就是 $\sum_{i=1}^n\frac{1}{i}\approx\ln n$;这样,复杂度就变为了 $O(nm+n\ln m\log S)$;
子集
考虑反演,反反反~其实反演是可以反演出一些东西来的,但是有点麻烦,直接讲正解好了。
首先将 $n$ 分解质因数:$n=\prod_{i=1}^np_i^{e_i}$;对于每个质因子分别考虑,设序列中每个数在这个质因子上的指数为 $a_i$,则题目等价于 $\min\{a_1,a_2,\cdots\}=0,\max\{a_1,a_2,\cdots\}=e$ ;
于是,现在题目的条件就被转化为一些稍微简单的限制条件了。由于 $1e18$ 以内的数不会有很多质因子(最多15个);考虑容斥,对于每个质因子,枚举四种情况(是否强制不满足第一个限制,是否强制不满足第二个限制),枚举后的计算比较简单,就是对于每个质因子计算指数上的取值范围,从而得到一共有多少个数满足这些限制,再计算这些数共能构成多少非空集合即可。这样的复杂度是 $4^{\omega(n)}$,稍微有点慢,不过可以得到80分,也算不错了;如何优化呢?可以发现,对于每个质因子,强制不满足一个限制时,$e$ 的取值有 $e_i$ 种,对容斥系数的贡献为$-1$,这两部分和"到底是哪个限制不满足"并没有关系,所以可以将"强制不满足第一个限制"和"强制不满足第二个性质"两种情况并在一起计算,最后将计算出的贡献 $\times 2$ 就好了;这样一来,复杂度就变成了 $3^{\omega(n)}$;其实甚至更小,因为当 $e_i=1$ 时,不能强制使两个限制都不满足,但如果 $e_i\neq 1$ 的情况较多,那么 $\omega(n)$ 就会更小;不过这并不重要,即使你没有注意到这一点,只要在搜索容斥条件时顺手剪个枝,达到的就是这个复杂度啦。
“不要学那些很酷很炫的算法,学好搜索剪枝才能成功。 ----loli”
最后一个小问题,怎么分解质因数?反正我直接 $Pollard~Rho$ 了...不过当然也有稍微简单的做法:可以发现,$p_i$ 是什么并不重要,我们只在乎 $e_i$ ;试除 $\leq \sqrt[3]{n}$ 的质数,这样剩下的部分一定是 $1,p,p^2,pq$ 四种情况,$1$ 显然不用管,对于其他三种情况计算指数,首先利用 $Miller-Rabin$ 判断是否是 $p$,然后开平方判断是否是 $p^2$ ,否则就是 $pq$ ;这样我们就得到了 $e$ 数组!
Day 3:

得分:100=60+10+30; rk:39;
比大小
对于一段连续的0/1,可以发现里面填的数必须是连续的一段。为什么呢?考虑从0切换到1或从1切换到0,会发现一定是先填满第 $i$ 列,再填第 $i+1$ 列,所以每一段填的数是哪些其实也是确定的;通过打表/推导可以发现长度为 $n$ 的一段的填数方案就是 $Cat_n$ ,段与段之间互不影响,所以最后把每一段的答案乘起来就好了。
玩游戏
首先这个题不能求出每棵树的sg函数再异或起来,因为每个游戏并不独立;通过一些思考,可以把树分成如下四类:先手可以强制使得走完这棵树后,再出发的是现在的后手;先手可以强制使得走完这棵树后,再出发的是现在的先手;先手可以强制使得走完这棵树后,再出发的是现在的先/后手(取决于先手意愿);先手不可以强制任何事;
首先,如果有一棵第三种树,那么先手一定必胜,因为先手可以一步走进这棵树,然后根据其它树形成局面是否必胜来切换先后手;第二种树没啥用,因为可以一上来就先把他们走完;以后我们的讨论中,默认没有第三种树,同时不考虑第二种树;一个显然的事实是,谁走进第四种树,谁就一定输掉整个游戏,这里的讨论和第一部分类似;所以先手一定是优先去走第一种树,然后选树的变成了后手,因为他也不想输,所以也是走第一种树;这样一来,最优策略等价于先走完所有的第一种树,再去走第四种树;最终的结论是:如果有奇数棵第一种树,同时没有第四种树,那么先手必胜;如果有偶数棵第一种树,同时存在第四种树,那么先手必胜;
数个数
$2^m$的容斥总是很简单的...
首先把所有包含了同一颜色其它区间的区间删掉,这样对于每种颜色,区间之间就不存在包含关系了;这种在序列上做容斥的题往往可以dp实现(虽然我不会),有的还可以用一个NTT什么的优化,总之挺神的。
设 $g_i$ 表示右端点 $\leq i$ 的所有限制所能构成的所有集合在[1,i]这段序列上所产生的贡献的和;是不是不大好理解? 举个例子吧,假设右端点 $\leq i$ 的限制有 $\{A,B\}$ 两个, 且它们共存(有交集,颜色相同或没有交集)。那么 $g_i$ 等于:不选任何限制的答案 $i^s$ +选了 $A$ 的答案 $(-1)^1\times (i-len_A)^s$+选了 $B$ 的答案 $(-1)^1\times (i-len_B)^s$+两个限制都选了的答案 $(-1)^2\times (i-len_{A\cup B})^s$;
现在开始做dp,按照右端点,顺次考虑每一个限制,并对于之前的所有限制集合计算这个新元素的贡献;虽然已经有了 $g$ 数组,但是还得设一个 $f_i$ 数组,意义与 $g$ 类似,但是有一点不同:钦定第 $i$ 个限制必选,计算的是 $[1,a_i.r]$ 这段序列贡献的和;首先,这个限制是可以不选的对吧... $g_i=s\times g_{i-1}$; 然后考虑选择这个限制的贡献,假设上一个选的限制不同色,那么两个限制不能有交集:$dp(i)+=(-1)\times g(a_i.l-1)$;假设上一个选的限制同色,那如果上个限制和它没有交集,刚刚就已经算过了,所以我们只枚举同色且有交集的限制,得到 $dp(i)+=(-1)\times \sum_{j}[i\cap j\neq \varnothing ][col_i==col_j]dp(j)$ ;这里的枚举不能暴力,而是要用双指针/前缀和;当然啦,还有最后一个转移: $g(a_i.r)+=dp(i)$;
Day 4:

得分:205=25+100+80; rk:19;
路径
其实这是一道构造题。对树进行一遍dfs,深度为奇数的点在进入时输出,深度为偶数的点在离开时输出就是一组合法方案了。
这样为什么是对的呢?考虑一个深度为奇数的点,他的上一个点只会是爷爷/兄弟/兄弟的儿子三种,而这三种情况的距离都是 $\leq 3 $ 的。对于一个深度为偶数的点,他的上一个点只会是父亲/孙子/兄弟三种,显然距离也都是 $\leq 3$ 的;
这道题有一点很好,就是:即使跳过了某个音节,那么与之相邻的两个音节也不会变得连续。
首先可以发现禁忌词不多,只有 $10$ 个,所以可以用 $hash$ 进行暴力匹配,得到所有不能连续出现的区间;为了方便处理,我们把所有包含了其他区间的区间去掉(注意:不是去掉所有被别的区间包含的区间),因为只要小区间没有连续出现,包含它的大区间就更不会连续出现了。经过这样的处理,再按照右端点进行排序,这些区间的左右端点就都是单调的了。
现在题目等价于:在数轴上选出一些位置,要求每个区间中至少要选一个点,求选出位置的权值和最小的方案;如果权值全相同的话,这就是一个经典的贪心问题,不过因为加权,问题变得稍微复杂了一点;可以想到的第一种方法是设 $dp(i)$ 表示前 $i$ 个区间都选了点的最优方案,但是,因为不知道这个方案是否覆盖了后面的区间,所以没法转移;既然如此,我们为什么不记录最后一个选的点呢?设 $dp(i)$ 表示最后选的点是 $i$ , $x$ 为 $i$ 能控制的最右边的区间, $[1,x]$ 的所有区间都已被控制的最小花费;然后就可以转移啦~设新加进一个点 $j$ ,首先右端点在 $j$ 前的区间中最靠右的那个,如果 $i$ 可以控制这个区间,那就说明 $dp(j)$ 可以从 $dp(i)$ 转移过来 。事实上,这个dp可以用一个单调队列优化,复杂度瓶颈在于字符串匹配和去掉包含区间时的那个排序。
首先,任意两条路径的交是 $P(u,v)$ $\neq$ 所有路径的交是 $P(u,v)$;这一点比较显然,但是也容易注意不到;
为了方便,我们先假装两个点不存在祖先关系,这样比较好想。因为任意两条路径的交是 $P(u,v)$,所以任意路径应该包含 $P(u,v)$,也就是说,路径的端点要么是 $u/v$,要么在 $u/v$ 的子树中;另一个显然的性质是,对于两条不同的路径,他们在 $u$ 这边的端点不会在 $u$ 的同一个儿子的子树里,$v$ 那边同理。设 $dp(x,y)$ 表示在 $x$ 的子树中(不包括 $x$ 这个点本身),选出 $y$ 个端点且满足条件的方案数。这非常简单,一个简单的背包就可以了。那么,总的方案数就是 $\left(\sum_{i=0}^Ldp(u,i)\times A(k,i)\right)\times\left(\sum_{i=0}^Ldp(v,i)\times A(k,i)\right)$;
啊,似乎还有一个问题?如果 $u,v$ 存在祖先关系怎么办?譬如 $u$ 是 $v$ 的祖先,那么,$v$ 的 $dp$ 数组不会变,而 $u$ 则要稍加变化:删去 $v$ 所在的那棵子树,将 $u$ 的“外部子树”(也就是整棵树去掉 $u$ 的子树的部分)作为新的子树加入;如果仔细想想,就会发现这个做法的实质:对于每一个点,我们求出以它为根时的 $dp$ 数组,当处理询问 $u,v$ 时,从 $dp(u)$ 中删去那棵包含 $v$ 的子树,从 $dp(v)$ 中删去那棵包含 $u$ 的子树。怎么删除呢?其实这也算是一个套路,“假面”那题我忘了写题解,所以就在这里仔细写一遍吧:原来的dp过程是
for (R i=k;i>=1;--i) dp[i]=(dp[i]+dp[i-1]*s);
也就是把 $\{a,b,c,d\}$ 变成了 $\{a,b+s\times a,c+s\times b,d+s\times c\}$;
那么我们把它反过来做一下,消除这个操作的影响,则有:
for (R i=1;i<=k;++i) dp[i]=(dp[i]-dp[i-1]*s);
注意两遍循环的顺序是反过来的,这是因为用来消除影响的 $dp$ 值自身也应该是消除过影响的。所以这道题的复杂度就是 $O(nL)$ 了。
Day 5:

得分:300=100+100+100; rk:3;
染色
首先,每个联通块是互不干扰的,所以我们只考虑一个联通块内部的情况;
如果一个联通块是树,那么它自己就会被染完,不用管;而对于一个环,却总是需要染一条边用于"启动"。考虑对于每个联通块找出一棵生成树,那么对于某条非树边 $(x,y)$,如果不染黑它,那么 $x,y$ 两点连接的其它边就不可能被自动染黑,这样显然不优;
现在,这道题的做法呼之欲出了:对于每个联通块找出一棵生成树后,答案即为非树边的数量总和;具体实现起来当然真的去找什么生成树,用并查集维护连通性就可以了;
乘方
第 $m$ 小的数字有一个套路的解决方法:二分,并看看比这个数小的是否有 $m-1$ 个;
如何计算 $S(t)$ 中有多少个数字小于我们目前 $check$ 的 $x$ ?答案就是 $\lfloor \sqrt[t]{x}\rfloor$ ;怎么求这个呢?接着二分吗?不行,二分后还要快速幂,两个 $\log$ 就太慢了,不如直接利用C++的pow函数来实现吧!虽然有点精度误差,但是求出答案后,稍微左移右移一两位判断一下是否合法就可以了,复杂度一个 $\log$(快速幂);
然而有一个问题...有的数可能会同时出现在多个 $S$ 中,这可怎么办呢?可以发现,如果一个数同时出现在 $a,b$ ,那么它也一定会出现在 $lcm(a,b)$ 处,我们在那里减掉它就好了;其实就是类似于一个容斥,这看上去很复杂,毕竟 $lcm$ 的范围是很大的,取值更是多种多样...不过呢,只要 $t>56$ ,那么 $S(t)$ 中 $\leq 10^{17}$ 的数就只有一个,根本不用考虑;也就是说,只需要考虑 $t\leq 56$ 的所有 $S(t)$ 就好了。这里不能靠 $dfs$ 来容斥(显然),可以通过一个简单的dp来计算每个 $S(t)$ 的容斥系数,这道题就做完了~
位运算
呃,这道题有一个简单粗暴的做法:$fwt,fwt,fwt$;直接卷出三个操作对应的数组,输出最大值及方案就好了....
然后讲一下它提供的正解吧。
Or:好像并没有什么很好的方法,官方题解也是 $fwt$ ;
Xor:依次插入每个数,并在 $0/1~Trie$ 上贪心求出最大答案;
And:从高位到低位贪心,如果当前位有 $\geq 2$ 个数是 $1$ ,那么最终答案的这一位就可以是 $1$,这时可以扫一遍,将所有这一位是 $0$ 的数扔掉,然后考虑下一位;否则直接考虑下一位;
Day 6:

得分:120=50+30+40; rk:9;
爬杆
这是一道笛卡尔树的题目...$csp-s$ 模拟赛 $T1$ 出这种题真的好么...
因为对于任意两个杆子,想要互相到达,总是要经过它们之间最矮的那根的,所以这道题看上去就跟“序列最小值”有着密不可分的关系;好吧,那我们先把笛卡尔树建出来。怎么建笛卡尔树呢?一个最简单的想法当然是用线段树维护区间最小值及位置,但是这次,我要介绍一种新的方法,可以 $O(n)$ 建出笛卡尔树;
序列笛卡尔树的性质显然有:权值满足堆的性质;中序遍历恰好是 $1 - n$ ;所以如果我们顺次将序列插入笛卡尔树,那么新加入的点 $x$ 一定会被加入到右边链的底部;但是还有权值的限制呢?在右链上从下往上找,找到第一个 $w_y<w_x$ 的点,就把 $x$ 接到 $y$ 处做右儿子,而原本 $y$ 的右子树则作为 $x$ 的左子树;找第一个 $w_y<w_x$ 的点很简单,因为右链上的值是单调的,所以类似单调栈来处理就好了;
for (R i=1;i<=n;++i) { while(tp&&h[i]<=h[ sta[tp] ]) ch[i][0]=sta[tp],tp--; if(tp!=0) ch[ sta[tp] ][1]=i; sta[++tp]=i; }
似乎我们已经建好了笛卡尔树~
现在我们来考察笛卡尔树上的某个节点 $x$ 以及它的左右儿子 $l(x),r(x)$,然后就不会了...
变换
没有,什么都没有;
游戏
其实,Bob必胜的条件是这棵树存在完美匹配;为什么?只要Alice把点放到某个点上,Bob就移到完美匹配处,这也算是另一种意义上的模仿棋了吧...
树的完美匹配是可以贪心来求的,所以我们设 $dp[i][j]$ 表示有多少种情况使得以i为根的子树贪心完后还未匹配的点有j个;仔细再回去读一遍定义!不要错误地理解成,有多少种匹配方式使得...别忘了这里是贪心匹配呀。那么dp就变得非常简单了。首先当然是对子树做背包,然后开始考虑根;如果选了i,那么 $dp[i][j]+=dp[i][j+1],dp[i][1]+=dp[i][0]$;
Day 7:

得分:75=0+60+15; rk:44;
Day 8:

得分:190=100+30+60;rk:30;
闯关
这道题是真的送分,引起极度舒适。首先可以观察到,前缀最小值序列是一个形如下降阶梯似的序列,而通关序列则是从后往前考虑每一个段,段内从前往后遍历而形成的序列;首先循环一遍,找到每一个段的开头,这个数一定是前缀最小值,对它的另一个限制是得给后面的每个前缀最小值留出取值空间。现在我们找到了所有的前缀最小值,假设有x个,为了字典序最小,我们从前往后分别填上 $x,x-1,x-2,\cdots$,这样显然合法。这时可以发现,因为剩下的数都比这些数大,所以怎么填都行,那么从小到大,从前往后就可以满足字典序最小的要求了。
动物园
这道题使我极度降智...
首先,将 $y$ 向 $x$ 连边,设 $dp[x][3]$ 分别表示这个数做完子树内操作后,动物的种类为 $0/1/2$ 的方案数;同时,对于这次询问的笼子所处的链稍微特殊处理即可。然而,然而,然而!这三种动物有本质区别吗?没有。三个dp数组的转移有本质区别吗?没有...所以这个dp数组非常没用...精简一波,你会发现转移全都是 $dp[x]*=dp[j]*k,k\in[1,2,3]$,这么想一想,可能就接近正解了。
换个角度来考虑,将合并关系建成树后,每个笼子最后都是要一直合并到根的,这其中,有一些次是主场合并,一些次是客场合并。而它的值和与它合并的值都是不定的,但概率都是$(\frac{1}{3},\frac{1}{3},\frac{1}{3})$,因为三种动物是没有区别的。也就是说,主场合并一次,胜出的概率为 $\frac{2}{3}$,客场合并一次,胜出的概率为 $\frac{1}{3}$;考虑将 $y$ 合并向 $x$,那么 $y$ 子树内的所有笼子都会多一次客场合并,$x$ 子树的所有笼子都会多一次主场合并,嗯,其实并查集是可以打标记的对吧...在 $x$ 处乘上一个 $\frac{2}{3}$,再在 $y$ 处乘上一个 $\frac{1}{3}$,将两者合并起来。这时,我们发现 $y$ 子树里的点多乘了 $w_x$,所以在 $w_y$ 处先行除掉就好了。
树
这道题十分有趣,用到了一个我没见过的结论:树的最大独立集可以贪心求;
首先选上所有儿子,然后删去被影响而不能选的点,不断进行这个操作,直到整棵树被选完,得到的就是最大独立集;为什么呢?首先,对于某个叶子,如果不选它,那么就有可能可以多选一个父亲,但是即使选上了这个父亲,独立集的大小也没有变大,同时,因为这个父亲可能不止一个儿子,有可能还会使答案变小;其次,选了叶子,那就不影响爷爷那层,不选叶子而选父亲,导致爷爷那层有些点也不能选了,所以也不如选叶子优;最后一点,因为叶子是没有儿子的,所以它和父亲必有一个被选,否则就不优。这样看来,贪心的确是对的。
再补充一点最大独立集的性质,以下设 $dp_0,dp_1$ 分别表示强制选或不选根时的最大独立集:
1.$dp_0\geq dp_1-1$;证明:考虑删掉根,将 $1$ 状态转变为 $0$ 状态;
对于原树进行两遍树形dp,求出以每个点为根时的最大独立集。等等,最大独立集和根是谁明明没有关系呀?确实没有关系,但是通过这样的dp,我们可以得到以每个点为根时,如果想得到最大独立集,需不需要选他。由于刚刚那个贪心的性质,可以发现每次新加的树一定是同时被删完的,所以选取情况也相同。如果新加的树必须要选根,那么 $T(k_i)$ 就没了,得到的 $T_i$ 相当于没选根,而答案则是 $n\times ans_{i-1}$;如果新加的树不选根,那么 $T(k_i)$ 不受任何影响,就按照最早的dp来即可,是否选根取决于一开始 $dp$ 的结果,答案等于 $n\times ans_{i-1}+dp$;
Day 9:

得分:120=0+20+100;rk:22;
Day 10:

得分:130=100+30+0;rk:23;
好吧...虽然这几场我一直在掉分,但是中间通过提高组十连测+普转提七连测上了93分,所以看上去还不算太惨;
旅行
这道题挺简单的,和“奶酪”有点像。看到最大值最小,可以想到二分一个值,看看每个点扩大这么多后,会不会把上下边界连起来;如果连起来了,那就无法通过了。其实,这就相当于找一条从下边界到上边界的路,使得最大值最小,这个过程可以用最小生成树实现;求最小生成树要用 $Prim$ 算法,因为只有它是 $k^2$ 的,其它算法都会超时;注意:不要一开始预处理所有的边,这样消耗时间过大,边做边算是一个不错的选择(因为有的边根本用不到,算出来纯属浪费);
寻宝
首先讲一下我一开始想的dp做法吧:设 $dp[i][j]$ 表示目前选了的点中,$x$ 最大的是第 $i$ 个点, $y$ 最大的是第 $j$ 个点时答案最大值的最小值;转移比较简单,因为一个点被重复加入并没有什么害处,所以枚举一个点加入这个状态就好了;复杂度 $n^3$ ,可以得到30分;
这时我想到,会不会贪心地加一个目前状态下代价最小的点就是最优解呢?于是我写了一个暴力尝试这个做法(但是我的暴力写错了!暴力写错了!)所以就以为这个结论是错的;其实是对的啦~考虑随便加入一个点,会不会使其它点加入时的代价变大呢?看看算贡献的式子就应该知道这不可能了;所以贪心地加就可以了;
那么问题来了,怎么贪心地加点呢?我们把点分为三类:在当前矩形上方的,在当前矩形右边的,在当前举行右上方的;这三类点互不包含,且每一类点计算答案的方式是相同的;我们可以弄三个堆,分别用来计算三类点的答案;好了,没时间了,下次再写吧~
鞋子
Day 11:


今天中途改了一次数据,所以rating变了两次;
得分:200=100+50+50;rk:3;
排行榜
搬箱子
改数字
Day 12:

得分:180=100+60+20;rk:20;
LIS
图论
防御
Day 13:

得分:100=30+50+20;rk:48;
二叉树
子序列
小游戏
Day 14:

本来想靠着周末两场比赛拯救一下的,结果提高组十连测再次跳水,幸好普转提抢救了一波;
得分:135=0+100+350;rk:14;
游戏
面积
删除
Day 15:

得分:135=100+20+15;rk:18;
这样都能上分?感觉自己打的很差啊?
字符串
显然,如果$[l,r]$是一个满足条件的子串,那么$[l,r+1]$就更是了,所以只要对于每个$l$求出最小的$r$就好了;发现虽然 $n$ 挺大,但是 $m$ 挺小,所以 $O(nm)$ 的算法就足以通过;这样,我们枚举 $l$ ,贪心地把 $m$ 匹配进去就好了;当然,这里的匹配复杂度只能是 $m$ ,否则就会超时,所以要预处理一个数组 $nex[i][j]$ 表示 $i$ 位置之后第一个 $j$ 字符的位置。
异或
生成树
Day 16:

行吧,又一夜回到解放前了;$\approx$ 这四场都没打;
得分:35=20+15+0;rk:30;
舔到
惨惨鸭!

因为一个并不成立的反例,导致我把正解删掉改成了暴力。然而考试计分按照最后一次提交...否则也能得到第六名的(哭
这道题可能需要一点灵感吧。将所有树分为两种:A:所有点的度数都为奇数的;B:至少一个点的度数是偶数的;
A在一次操作后一定会变成B,而B至少有一种方法变成A(因为是一棵树,从叶子往上找,找到第一个度数为偶数的,断掉它和根就好了;如果第一个度数为偶数的点就是根,那么随便断掉一棵子树);看上去,这正好符合博弈论的必败态,必胜态;再考虑一下,发现只有一个点的边界情况属于B,且是必胜态;那么,A就是必败态,B就是必胜态了;
没有代码
最后
一无所有
Day 17:


真·稳得不行;
得分:130=100+0+30;rk:15;
红黑树
设 $dp[i][j][0/1]$ 表示以 $i$ 为根的子树中,所有空节点到 $i$ 会经过 $j$ 个黑点,$i$ 涂成了红或黑是否可行;转移显然...输出方案时,再跑一遍dp,按照转移构造方案即可。
旅行
数字
Day 18:

得分:60=0+40+25;rk:30;
视频
图论
排队
Day 19:

是真的不容易啊,终于开始上分了...
得分:130=100+30+0;rk:13;
象棋
首先让我们给斜线编号!
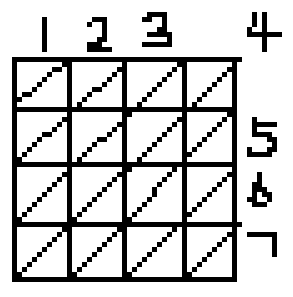
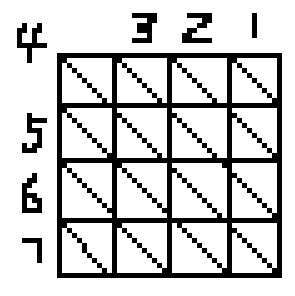
第一种对角线横纵坐标的和相同,第二种对角线横纵坐标的差相同,所以我们可以很容易的算出每个棋子在哪两条对角线上,从而得到每条对角线是否被覆盖;
现在开始计算有多少个点没有被覆盖:首先按照编号从小到大枚举第一种对角线,然后枚举与它相交的第二种对角线;1->4,2->{3,5},3->{2,4,6},可以发现,随着第一种对角线编号的增加,第二种对角线的选择区间也在不断扩大,同时,只有奇偶性不同的斜线才会相交;可能有一点点小细节,总之这题还是挺简单的;
咕咕咕
序列
Day 20:

Extra-1:


