$Codeforces$ $Global$ $Round$ $1$
\(Codeforces\) \(Global\) \(Round\) \(1\)
看到CF首页上有\(global\) \(round\) \(3\)的通知,虽然没时间打,但是做做之前的场次还是OK的。
\(A.Parity\)
题意概述:以 \(b\) 进制给出一个数,求它在十进制下的奇偶性。
比较水,没什么好说的,按位判断即可。
# include <cstdio>
# include <iostream>
# define R register int
using namespace std;
int b,k,x;
int ans;
int main()
{
scanf("%d%d",&b,&k);
for (R i=1;i<k;++i)
{
scanf("%d",&x);
if(b%2==0||x%2==0) continue;
ans++;
}
scanf("%d",&x);
if(x%2) ans++;
if(ans%2) puts("odd");
else puts("even");
return 0;
}
\(B.Tape\)
题意概述:你有一条长度为 \(m\) 的带子,但是 \(n\) 处破掉了,所以要用另一条来补上,你可以从另一条带子上截取任意长度用来补充,但是最多只能截取 \(k\) 段,求最小的总长度。\(k<=n<=10^5,m<=10^9\)
如果不考虑只能截取 \(k\) 段的限制,那么每个破处打一个补丁就可以了,现在的问题是怎么把 \(n\) 个补丁转化成 \(k\) 个。只要把两个漏洞之间的部分也打上补丁,那么补丁的段数就会减少一,所以只需要将相邻的补丁间的长度都算出来,从小往大里连,连到段数符合要求即可。
# include <cstdio>
# include <iostream>
# include <queue>
# define R register int
# define ll long long
using namespace std;
const int maxn=100005;
int n,m,k,b[maxn];
ll ans;
priority_queue <int,vector<int>,greater<int> > q;
int main()
{
scanf("%d%d%d",&n,&m,&k);
ans=n;
for (R i=1;i<=n;++i)
scanf("%d",&b[i]);
for (R i=1;i<n;++i)
q.push(b[i+1]-b[i]-1);
for (R i=1;i<=n-k;++i)
ans+=q.top(),q.pop();
cout<<ans;
return 0;
}
\(C. Meaningless ~Operations\)
题意概述:定义一个这样的函数:$f(a) = \max_{0 < b < a}{gcd(a \oplus b, a > & > b)}. $,给出 \(q\) 个 \(a\),请求出 \(f(a)\),\(q<=10^3,2<=a<=2^{25}-1\)
本题看起来奥妙重重,但是样例可以给我们一点提示。
可以发现,如果一个数的二进制位不全是1,那么让b来将这些空补上是最好不多的了。这样,异或值就是11..1的形式,与的值就是0,最大公约数就是异或值。因为b不能超过a,所以这显然就是最好的方案了。
如果一个数的二进制位全是1又怎么办呢?打表啊...当然也有一个正经做法:在这种情况下,可以认为\(f(x)=gcd(a-b,b)\),所以可以取到x的最大真因子;
# include <cstdio>
# include <iostream>
# include <map>
# define R register int
using namespace std;
int x,q;
map <int,int> m;
int m2[100];
int main()
{
scanf("%d",&q);
m[1]=0; m[3]=1; m[7]=1; m[15]=5; m[31]=1; m[63]=21; m[127]=1; m[255]=85; m[511]=73; m[1023]=341;
m[2047]=89; m[4095]=1365; m[8191]=1; m[16383]=5461; m[32767]=4681; m[65535]=21845;
m[131071]=1; m[262143]=87381; m[524287]=1; m[1048575]=349525; m[2097151]=299593;
m[4194303]=1398101; m[8388607]=178481; m[16777215]=5592405; m[33554431]=1082401;
for (R i=2;i<=26;++i) m2[i]=(1<<i)-1;
while(q--)
{
cin>>x;
if(m[x]) cout<<m[x]<<endl;
else
{
int l=0;
while(x!=0) { x/=2,l++; }
cout<<m2[l]<<endl;
}
}
return 0;
}
\(D.Jongmah\)
题意概述:给出n块瓷砖,每块有一个介于 \([1,m]\) 的大小,要将它们做成一些“三倍”(我也不知道这题在说些啥),一个“三倍”可以是这样的形式[x-1,x,x+1],也可以是[x,x,x]。求出最多能做几个“三倍”。\(n<=10^6,m<=10^6\)
有两种比较简单的贪心思路:先凑第一种,再凑第二种。或者反过来。
可惜,这两种做法都不对,给两组反例吧:
1 1 1 2 2 2 3 3 3,答案为3;
1 1 2 2 2 2 3 3 3 3 3 3 4 4 4 4 5 5,答案为6;
如果想要dp,可以这样设置状态:\(dp[i][j][k]\) 表示当前dp到i这种瓷砖,上一种和再上一种各剩下多少张时最多的“三倍”数量。但是空间又开不下。
正解是用贪心的思想优化dp状态。
既然问题在于空间不够,而 \(i\) 一维显然没有优化空间,所以我们希望减少 \(j\),\(k\) 两维的上界。可以发现凑三个 \([x-1,x,x+1]\) 不如转化为 \([x-1,x-1,x-1]\) , \([x,x,x]\) , \([x+1,x+1,x+1]\),同一种连号最多只需要凑两组。这样一来,每种瓷砖需要留下的块数也就少了很多,可以进行dp了。
# include <cstdio>
# include <iostream>
# include <cstring>
# define R register int
using namespace std;
const int maxn=1000006;
int n,m,x,ans;
int t[maxn],dp[maxn][5][3];
inline void giv (int x,int y,int z,int v)
{
if(y>=6) dp[x][y-3][z]=max(dp[x][y-3][z],v+1);
dp[x][y%3][z%3]=max(dp[x][y%3][z%3],v+(y/3)+(z/3));
dp[x][min(y,4)][z%3]=max(dp[x][min(y,4)][z%3],v+z/3);
dp[x][y%3][min(z,2)]=max(dp[x][y%3][min(z,2)],v+y/3);
dp[x][min(y,4)][min(z,2)]=max(dp[x][min(y,4)][min(z,2)],v);
}
int main()
{
scanf("%d%d",&n,&m);
for (R i=1;i<=n;++i) scanf("%d",&x),t[x]++;
memset(dp,-1,sizeof(dp)); dp[0][0][0]=0;
for (R i=1;i<=m;++i)
if(t[i]>6) x=(t[i]-6)/3,t[i]=t[i]-3*x,ans+=x;
for (R i=1;i<=m;++i)
for (R j=0;j<=4;++j)
for (R k=0;k<=2;++k)
{
if(dp[i-1][j][k]==-1) continue;
int a=dp[i-1][j][k];
if(t[i]>=2&&j>=2&&k>=2) giv(i,t[i]-2,j-2,a+2);
if(t[i]>=1&&j>=1&&k>=1) giv(i,t[i]-1,j-1,a+1);
giv(i,t[i],j,a);
}
int fans=0;
for (R i=0;i<=4;++i)
for (R j=0;j<=2;++j)
fans=max(fans,dp[m][i][j]);
printf("%d",fans+ans);
return 0;
}
\(E.Magic~Stones\)
题意概述:给定两个长度为 \(n\) 的数列 \(s\) 和 \(t\) ,可以对 \(s\) 数列做这样一种操作:将不在两端的一个数 \(c_i\) 变成\(c_{i+1}+c_{i-1}-c_i\) ,求是否可以通过一些方法使得 \(s\) 变成 $t $。
\(n\leq 10^5,c_i\leq 2\times 10^9\)
这道题比较有趣,可能需要一点灵感。考虑将 \(s\),\(t\) 分别差分,发现操作前后分别是这样的:
\(a~b ~c~\rightarrow ~b-a~~c-b\)
\(a~~a+c-b~~c\rightarrow c-b~~b-a\)
也就是说,一次操作只不过是把差分数组的两个值进行了一次交换。所以只要比较两个数列的差分数组是否可以一一对应即可。注意:第一个数需要特判一下是否相等,因为不能对它进行任何操作。
# include <cstdio>
# include <iostream>
# include <algorithm>
# define R register int
using namespace std;
const int maxn=100005;
int n,x,las,b1,e1,b2,e2;
int c[maxn],t[maxn];
int main()
{
scanf("%d",&n);
scanf("%d",&las); b1=las;
for (R i=2;i<=n;++i)
{
scanf("%d",&x);
if(i==n) e1=x;
c[i-1]=x-las; las=x;
}
scanf("%d",&las); b2=las;
for (R i=2;i<=n;++i)
{
scanf("%d",&x);
if(i==n) e2=x;
t[i-1]=x-las; las=x;
}
sort(c+1,c+n);
sort(t+1,t+n);
for (R i=1;i<n;++i)
{
if(c[i]!=t[i])
{
puts("No");
return 0;
}
}
if(e1!=e2||b1!=b2) puts("No");
else puts("Yes");
return 0;
}
\(F. Nearest~Leaf\)
题意概述:给定一棵带权有根树,且每个节点的编号是按照欧拉序编好的。给出 \(q\) 组询问,每次询问形如:在编号在 \([l,r]\) 范围内的叶子里,与 \(x\) 最近的距离是多少?
\(3\leq n\leq 500000,1 \leq q \leq 500000\)
乍一看,这道题好像可以分块预处理答案,然而空间时间都不是很够。考虑抄题解。
发现题目给出了一个性质(节点的编号是按照欧拉序编好的),这是什么意思呢?通过仔细阅读题面,发现它的意思就是 \(dfs\) 序...
考虑离线,维护目前点到每个叶子的距离。比方说,\(x\) 是 \(y\) 的父亲,他们之间那条边的边权是 \(w\),如果从 \(x\) 走到 \(y\) ,不在 \(y\) 子树里的叶子的距离就会增加 \(w\),而在 \(y\) 子树里的叶子的距离就会减少 \(w\)。因为一棵子树里的叶子的编号是连续的。我们要做的就是区间修改,区间查询最小值,用一棵线段树就可以实现。
# include <cstdio>
# include <iostream>
# include <cstring>
# include <cmath>
# include <vector>
# define R register int
# define LL long long
# define nl (n<<1)
# define nr (n<<1|1)
using namespace std;
const int maxn=500005;
int n,q,h,firs[maxn],d[maxn],las[maxn],f,v,x;
LL t[maxn<<2],delta[maxn<<2],dis[maxn];
struct edge { int too,nex; LL v; }g[maxn];
struct ask { int l,r; LL ans; }as[maxn];
vector <int> s[maxn];
void add (int x,int y,LL v)
{
g[++h].too=y;
g[h].nex=firs[x];
g[h].v=v;
firs[x]=h;
}
int dfs (int x)
{
int j,ans=x;
for (R i=firs[x];i;i=g[i].nex)
{
j=g[i].too;
dis[j]=dis[x]+1LL*g[i].v;
ans=max(ans,dfs(j));
}
las[x]=ans;
return ans;
}
void build (int n,int l,int r)
{
if(l==r)
{
if(d[l]!=1) t[n]=1e15;
else t[n]=dis[l];
return;
}
int mid=(l+r)>>1;
build(nl,l,mid);
build(nr,mid+1,r);
t[n]=min(t[nl],t[nr]);
}
void pushdown (int n)
{
LL v=delta[n]; delta[n]=0;
delta[nl]+=v; t[nl]+=v;
delta[nr]+=v; t[nr]+=v;
}
void add (int n,int l,int r,int ll,int rr,LL v)
{
if(ll<=l&&r<=rr)
{
delta[n]+=v;
t[n]+=v;
return;
}
int mid=(l+r)>>1;
if(delta[n]) pushdown(n);
if(ll<=mid) add(nl,l,mid,ll,rr,v);
if(rr>mid) add(nr,mid+1,r,ll,rr,v);
t[n]=min(t[nl],t[nr]);
}
LL ask (int n,int l,int r,int ll,int rr)
{
if(ll<=l&&r<=rr) return t[n];
int mid=(l+r)>>1; LL ans=1e17;
if(delta[n]) pushdown(n);
if(ll<=mid) ans=min(ans,ask(nl,l,mid,ll,rr));
if(rr>mid) ans=min(ans,ask(nr,mid+1,r,ll,rr));
return ans;
}
void redfs (int x)
{
int siz=s[x].size(),j;
for (R i=0;i<siz;++i)
{
j=s[x][i];
as[j].ans=ask(1,1,n,as[j].l,as[j].r);
}
for (R i=firs[x];i;i=g[i].nex)
{
j=g[i].too;
add(1,1,n,1,n,g[i].v);
add(1,1,n,j,las[j],-2*g[i].v);
redfs(j);
add(1,1,n,1,n,-g[i].v);
add(1,1,n,j,las[j],2*g[i].v);
}
}
int main()
{
scanf("%d%d",&n,&q);
for (R i=2;i<=n;++i)
{
scanf("%d%d",&f,&v);
add(f,i,v);
d[f]++; d[i]++;
}
dfs(1);
build(1,1,n);
for (R i=1;i<=q;++i)
{
scanf("%d%d%d",&x,&as[i].l,&as[i].r);
s[x].push_back(i);
}
redfs(1);
for (R i=1;i<=q;++i)
printf("%I64d\n",as[i].ans);
return 0;
}
\(G.Tree-Tac-Toe\)
题意概述:在树上玩井字棋。给定一棵树,树上有一些点已经放上白棋,其它点没有颜色,白色先手,轮流落子,如果某个颜色形成了一个大小至少为 \(3\) 的联通块,那么它就赢了。问在最优策略下,是"白色必胜"还是"黑色必胜"还是"平局"。
\(1\leq n\leq 5 \times 10^5\)
这道题的小细节还是挺多的。
首先如果树的大小不到3,那肯定平局了。如果树的大小恰好等于3,而且白色不能第一子就赢的话,还是平局。
一个显然的事实是,黑色绝不可能胜利。为什么呢?因为在没有一开始就放好的白棋的情况下,整个棋盘(棋树)对于两个棋手来说是一模一样的,而这又不属于一般的平等博弈问题,白子不可能在任何意义下给黑棋帮助,所以先手一定是比后手有优势的。如果考虑到已经有了一些白棋...那不还是先手的优势吗。
先考虑没有白棋的情况:
1.某个点的度数大于等于\(4\),白棋必胜。(白棋下在中间那个点上,黑棋不可能在两步之内挡住所有路)
2.某个点的度数等于 \(3\),但是最多只连向一个叶子,白棋必胜。(白棋下在中间那个点上,黑棋如果童谣无法在两步内把路全挡上);
排除掉这几种情况后,树只有三种形态:链,\(Y\) 字形,\(>---<\) 形。
前两种显然是平局了,但是在最后一种情况里,如果总点数为奇数,那么白色也是必胜的。
看起来问题好像解决的挺完美,但是还有一个问题:原来就是白色的点呢?
如果我们把一个原来就是白色的点称为 \(A\) ,那么就往它下面再连上这么一个东西:
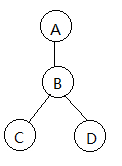
这样,就可以把原来是白色的点转变成无色了。聪明的白色可以先在 \(A\) 上下棋,此时黑色必须在 \(B\) 上下,然后他们就会发现 \(CD\) 两个点都没有任何意义了,也就达到了钦定白色的功能。
# include <cstdio>
# include <iostream>
# include <cstring>
# define R register int
using namespace std;
const int maxn=2000006;
int t,n,cnt,h,firs[maxn],a,b,d[maxn],y[maxn];
char s[maxn];
struct edge { int too,nex; }g[maxn<<1];
void add (int x,int y)
{
g[++h].too=y;
g[h].nex=firs[x];
firs[x]=h;
d[x]++; d[y]++;
}
int main()
{
scanf("%d",&t);
while(t--)
{
memset(firs,0,sizeof(int)*(cnt+5));
memset(d,0,sizeof(int)*(cnt+5));
memset(y,0,sizeof(int)*(cnt+5));
scanf("%d",&n); h=0,cnt=n;
for (R i=1;i<n;++i)
{
scanf("%d%d",&a,&b);
add(a,b); add(b,a);
}
scanf("%s",s+1);
for (R i=1;i<=n;++i)
if(s[i]=='W')
{
++cnt; add(i,cnt),add(cnt,i);
++cnt; add(cnt,cnt-1),add(cnt-1,cnt);
++cnt; add(cnt,cnt-2),add(cnt-2,cnt);
}
if(n<3) { puts("Draw"); continue; }
if(n==3)
{
int wt=0;
for (R i=1;i<=n;++i) if(s[i]=='W') wt++;
if(wt>=2) puts("White");
else puts("Draw");
continue;
}
int ans=0,k;
for (R i=1;i<=cnt;++i) if(d[i]>6) ans=1;
for (R i=1;i<=cnt;++i)
{
if(d[i]==2) continue;
for (R j=firs[i];j;j=g[j].nex)
{
k=g[j].too;
y[k]++;
}
}
for (R i=1;i<=cnt;++i)
if(d[i]==6&&y[i]>=2) ans=1;
int nct=0;
for (R i=1;i<=cnt;++i)
if(d[i]==6&&y[i]==1) nct++;
if(nct==2&&(cnt%2)) ans=1;
if(ans) puts("White"); else puts("Draw");
}
return 0;
}
\(H.Modest~Substrings\)
题意概述:给定两个数字 \(l\),\(r\),要求构造一个长度为 \(n\) 的字符串,使得其中有最多的子串连起来后构成的数字满足 \(l\leq x \leq r\)。输出答案和这个字符串。
\(l,r\leq 10^{800},n\leq 2000\)
我感觉这题比较神。
如果 \(l,r\) 比较小,那么可以把所有满足条件的数插入AC自动机,在AC自动机上进行dp。可是\(l,r\)非常的大,这样做就不是很OK。如果还是想把他们插入AC自动机,自动机里就会有很多的满十叉树。既然是满十叉树,也就是说之后填什么都没关系,只要长度对就可以了。那么,不如把这部分直接略去,而是在树根处加一些“x-通配符”,意思是从这里往后任意填 \(x\) 个字符都可以构成一个满足条件的子串。当 \(dp\) 到这里的时候,看看剩下的长度够不够 \(x\) ,如果够的话就在这里提前加上贡献。想明白了其实也不算很难,但是思路比较妙。
注意:建议对通配符数组进行前缀和来优化复杂度,通配符数组可以通过 \(fail\) 指针来继承。
//This code is written by shzr
# include <cstdio>
# include <iostream>
# include <cstring>
# define R register int
using namespace std;
const int maxn=2005;
const int maxz=16005;
int l[maxn],r[maxn],n,l1,l2;
int dp[maxn][maxz],q[maxz];
bool lt[maxn][maxz];
char s[maxn];
struct ac_machine
{
int ch[maxz][10],cnt;
int fail[maxz];
int tp[maxz][maxn];
void init()
{
int x=0,y=0;
if(l1==l2)
{
for (R i=1; i<=l1; ++i)
{
if(x==y) {
for (R j=l[i]+1; j<r[i]; ++j)
{
if(!ch[x][j]) ch[x][j]=++cnt;
tp[ ch[x][j] ][ l1-i ]++;
}
} else
{
for (R j=l[i]+1; j<=9; ++j)
{
if(!ch[x][j]) ch[x][j]=++cnt;
tp[ ch[x][j] ][ l1-i ]++;
}
for (R j=(i==1); j<r[i]; ++j)
{
if(!ch[y][j]) ch[y][j]=++cnt;
tp[ ch[y][j] ][ l2-i ]++;
}
}
if(!ch[x][ l[i] ]) ch[x][ l[i] ]=++cnt;
x=ch[x][ l[i] ];
if(!ch[y][ r[i] ]) ch[y][ r[i] ]=++cnt;
y=ch[y][ r[i] ];
}
tp[x][0]++;
if(x!=y) tp[y][0]++;
} else
{
for (R i=1; i<=l1; ++i)
{
for (R j=l[i]+1; j<=9; ++j)
{
if(!ch[x][j]) ch[x][j]=++cnt;
tp[ ch[x][j] ][ l1-i ]++;
}
if(!ch[x][ l[i] ]) ch[x][ l[i] ]=++cnt;
x=ch[x][ l[i] ];
}
for (R i=1; i<=l2; ++i)
{
for (R j=(i==1); j<r[i]; ++j)
{
if(!ch[y][j]) ch[y][j]=++cnt;
tp[ ch[y][j] ][ l2-i ]++;
}
if(!ch[y][ r[i] ]) ch[y][ r[i] ]=++cnt;
y=ch[y][ r[i] ];
}
for (R i=l1+1; i<l2; ++i)
for (R j=1; j<=9; ++j)
{
if(!ch[0][j]) ch[0][j]=++cnt;
tp[ ch[0][j] ][i-1]++;
}
tp[x][0]++;
tp[y][0]++;
}
}
void build()
{
int h=1,t=0;
for (R i=0; i<=9; ++i)
if(ch[0][i])
q[++t]=ch[0][i];
int x;
while(h<=t)
{
x=q[h++];
for (R i=0; i<=9; ++i)
if(!ch[x][i]) ch[x][i]=ch[ fail[x] ][i];
else fail[ ch[x][i] ]=ch[ fail[x] ][i],q[++t]=ch[x][i];
}
for (R i=1; i<=t; ++i)
{
x=q[i];
for (R j=0; j<=n; ++j)
tp[x][j]+=tp[ fail[x] ][j];
}
for (R i=1; i<=cnt; ++i)
for (R j=1; j<=n; ++j)
tp[i][j]+=tp[i][j-1];
}
} t;
int main()
{
t.cnt=0;
scanf("%s",s+1);
l1=strlen(s+1);
for (R i=1; i<=l1; i++) l[i]=s[i]-'0';
scanf("%s",s+1);
l2=strlen(s+1);
for (R i=1; i<=l2; i++) r[i]=s[i]-'0';
scanf("%d",&n);
memset(dp,-1,sizeof(dp));
dp[0][0]=0;
t.init();
t.build();
for (R i=0; i<n; ++i)
for (R j=0; j<=t.cnt; ++j)
{
if(dp[i][j]==-1) continue;
for (R k=0; k<=9; ++k)
{
int x=t.ch[j][k];
dp[i+1][x]=max(dp[i+1][x],dp[i][j]+t.tp[x][n-i-1]);
}
}
int ans=0;
for (R i=0; i<=t.cnt; ++i) ans=max(ans,dp[n][i]);
printf("%d\n",ans);
for (R i=0; i<=t.cnt; ++i) if(dp[n][i]==ans) lt[n][i]=1;
for (R i=n-1; i>=0; --i)
{
for (R j=0; j<=t.cnt; ++j)
{
if(dp[i][j]==-1) continue;
for (R k=0; k<=9; ++k)
{
int x=t.ch[j][k];
lt[i][j]|=lt[i+1][x]&&(dp[i+1][x]==dp[i][j]+t.tp[x][n-i-1]);
}
}
}
int x=0;
for (R i=0; i<n; ++i)
{
for (R j=0; j<=9; ++j)
{
int y=t.ch[x][j];
if(lt[i+1][y]&&(dp[i+1][y]==dp[i][x]+t.tp[y][n-i-1]))
{
putchar(j+'0');
x=y;
break;
}
}
}
return 0;
}



